电子科技大学：《高等电磁场理论》课程教学资源（课件讲稿）第六章 电磁散射

第六章 电磁散射 古等电赋场理论 将入射波按柱面波函数展开： ●● E'=ek=epcose=∑(-)”Jn(kp)em 1n=-00 由(E'+Eoa=0→∑[a,H2(ka)+(-）J,(kaem=0 n=-00 →anH2(ka)+(-j)”Jn(ka）=0 →a,=-(" J (ka) H(ka) 故得到 E-()2 H2(ka) HO(kp)e

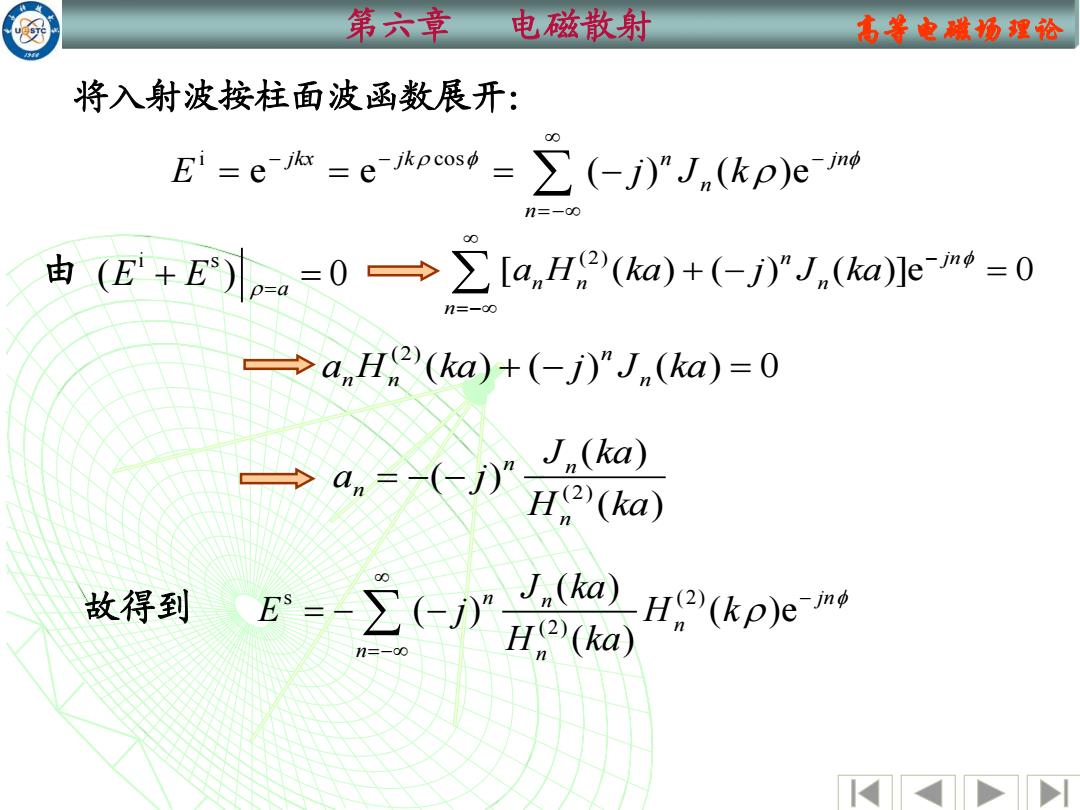
第六章 电磁散射 高等电磁场理论 将入射波按柱面波函数展开： i cos e e ( ) ( )e jkx jk n jn n n E j J k      − − − =− = = = −  i s ( ) 0 由 E E + = =a (2) ( ) ( ) ( ) 0 n n n n a H ka j J ka + − = 故得到 s (2) (2) ( ) ( ) ( )e ( ) n jn n n n n J ka E j H k H ka    − =− = − −  (2) ( ) ( ) ( ) n n n n J ka a j H ka = − − (2) [ ( ) ( ) ( )]e 0 n jn n n n n a H ka j J ka   − =−  + − =

第六章 电磁散射 名等电城场理论 ★讨论： ① 远区散射场kp>1→ H(k -e 2 单位长度的散射截面：o=1im2πp ② 低频散射：ka<<1 y3 n=0 →.a)空月 a-- n≠0 散射截面中n=0为主要项，则 J(ka) H(ka) kIn2(ka/2)

第六章 电磁散射 高等电磁场理论 ★ 讨论： 单位长度的散射截面: k 1 π π ( ) (2) 2 4 2 ( ) e π j k n H k n k    − − − s 2 2 i (2) 4 ( ) lim 2π e ( ) n jn n n E J ka E k H ka      − →  =− = =  ① 远区散射场 s (2) e 2 ( ) e π ( ) jk n jn n n j J ka E k H ka    −  − =− = −  散射截面中n=0为主要项，则 ② 低频散射： ka  1 1 ( ) ( ) ! 2 n n ka J ka n ( 2 ) 2 ln( ) 0 π 2 ( ) ( 1)!( ) 0 π 2 n n ka j n H ka n ka j n −  − =   −  −   2 2 (2) 2 4 ( ) π e ( ) ln ( / 2) n jn n n J ka k H ka k ka    − =− =  

第六章 电磁散射 古等电赋场理论 2. 理想介质圆柱对平面波的散射 ① 散射体为介质圆柱(E=e.ex) 圆柱内(p<a）E,=e.∑bnJn(kp)e n=-00 E 月x店 joμ 圆柱外(p>a)E=∑anH2(kp)em E,=e.(E+E,五，=-V×E, jouo 边界条件：(E,-E2)p。=0,(H。-H26)。a=0 b

第六章 电磁散射 高等电磁场理论 ( 2 ) 2 0 ( )e s jn n n n E a H k    − =− =  1 1 1 H E j = −   1 ( )e jn z n n n E e b J k    − =− 圆柱内 ( )   a =  i 2 2 2 2 0 1 ( ), s E e E E H E z j = + = −   ① 散射体为介质圆柱 0 i ( e ) jk x E e z − = 边界条件： 1 2 ( ) 0, E E − = =a 1 2 ( ) 0 H H    − = =a 圆柱外 ( )   a x y   a  i E 0 k n n a b  =  =  2. 理想介质圆柱对平面波的散射

第六章 电磁散射 名等电赋场理论 ② 导体圆柱表面涂介质层(E=e.eox) 介质内(a<p<b) E=e.[b J(kp)+cN,(kp)le-m n=-00 人 i1=-V×E jou 介质外(p>b)E=∑anH%2(kp)em n=-00 E2=e(E+E),1 ,=-1v×E jouo 边界条件：Eoa=0,(E,-E)b=0,(H。-H)b=0 an=…,bn=…

第六章 电磁散射 高等电磁场理论 ( 2 ) 2 0 ( )e s jn n n n E a H k    − =− =  1 [ ( ) ( )]e jn z n n n n n E e b J k c N k     − =− = +  ② 导体圆柱表面涂介质层 0 i ( e ) jk x E e z − = i s 2 2 2 2 0 1 ( ), E e E E H E z j = + = −   介质外 ( )   b 介质内 ( ) a b    边界条件： 1 2 ( ) 0, E E − = =b 1 2 ( ) 0 E1 =a = 0, H H    − = =b x y  a  i E 0 k b 1 1 1 H E j = −   , , n n n a b c = = =

第六章 电磁散射 古等电赋场理论 3.平面波对理想导体圆柱的斜入射 ① 已知入射波电场为E=e,ek+) 今H=(ek-e,k)e ouo E。= oH 1 02H. josp dd Ho= k2 0poz 1 E OH: 1∂2H. j080p H。=- k2p 8982 H!= ke,)三 e∑(-)”J,(k.pe @uo 0' n=-0 设H=ke:2a,Hg2(kpe 04o n=-0o 8(H:+H:) =0→a,=-(y2k ap p=a HO(k,a)

第六章 电磁散射 高等电磁场理论 ① 已知入射波电场为 i ( ) e x z j k x k z E e y − + = 由 i ( ) 0 e x z x j k x k z z k H  − + = i ( ) 0 1 ( )e x z j k x k z H e k e k z x x z  − +  = − s (2) 0 e ( )e z x jk z jn z n n x n k H a H k      − − =− =  x z a i E  i H i k 3. 平面波对理想导体圆柱的斜入射 0 e ( ) ( )e z x jk z n jn n x n k j J k      − − =− = −  设 1 1 z z H E j H E j         =       = −   2 2 2 2 1 1 z z H H k z H H k z        =        = −     s ( ) 0 0 i z z a a H H E    = =  + = =   (2) ( ) ( ) ( ) n n x n n x J k a a j H k a  = − − 