
课程名称:运筹学 专业:信息管理与信息系统 班级: min(-Z)=-3x+2x2-4(x-x+0x+0x+0x。 2x1+3x2+4(x1-x)-x42300 s1. x+5x3+6(x,-x)+x≤400 x+x2+x-x+x。≤200 x,2,x,x,x,x,x620 学生阵可, 将线性规划问题化为标准型: minZ =x+2x2 3x1-8x2≤5 x1-3x2≥4 x1≥0,x2无约束 解: marZ'=x,-26,-x4) 3x1-863-x4+x5=5 x1-36-x-x6=4 x1,X3x4X5,x620 8、线性规划问题的解 可行解:满足约束条件的解为可行解。所有可行解的集合为可行域, 最优解:使目标函数达到最大值的可行解。 基:设A为约束条件②的mXn阶系数矩阵(m<),其秩为m,B是矩阵A中m阶 满秩子矩阵(|B|≠0),称B是规划问题的一个基。 基解:某一确定的基B,令非基变量等于零,由约束条件方程②解出基变量,称这 组解为基解。在基解中变量取非0值的个数不大于方程数m,基解的总数不超过 基可行解:满足变量非负约束条件的基本解,简称基可行解。 可行基:对应于基可行解的基称为可行基
课程名称:运筹学 专业:信息管理与信息系统 班级: 9 ' '' 1 2 3 3 4 5 6 ' '' 1 2 3 3 4 ' '' 1 2 3 3 5 ' '' 1 2 3 3 6 ' '' 1 2 3 3 4 5 6 min( ) 3 2 4( 0 0 0 2 3 4( ) 300 5 6( ) 400 . . 200 , , , , , , 0 Z x x x x x x x x x x x x x x x x x s t x x x x x x x x x x x x − = − + − − + + + + + − − + + − + + + − + 学生练习: 将线性规划问题化为标准型: − − = + 1 2无约束 1 2 1 2 2 0, 3 4 3 8 5 2 x x x x x x minZ -x1 x 解: − − − = − − + = = − − x ,x ,x ,x ,x 0 x (x x ) x x (x x ) x max Z x (x x ) 1 1 1 1 3 4 5 6 3 4 6 3 4 5 3 4 3 4 3 8 5 2 8、线性规划问题的解 可行解:满足约束条件的解为可行解。所有可行解的集合为可行域。 最优解:使目标函数达到最大值的可行解。 基:设 A 为约束条件②的 m×n 阶系数矩阵(m<n),其秩为 m,B 是矩阵 A 中 m 阶 满秩子矩阵(∣B∣≠0),称 B 是规划问题的一个基。 基解:某一确定的基 B,令非基变量等于零,由约束条件方程②解出基变量,称这 组解为基解。在基解中变量取非 0 值的个数不大于方程数 m,基解的总数不超过 基可行解:满足变量非负约束条件的基本解,简称基可行解。 可行基:对应于基可行解的基称为可行基
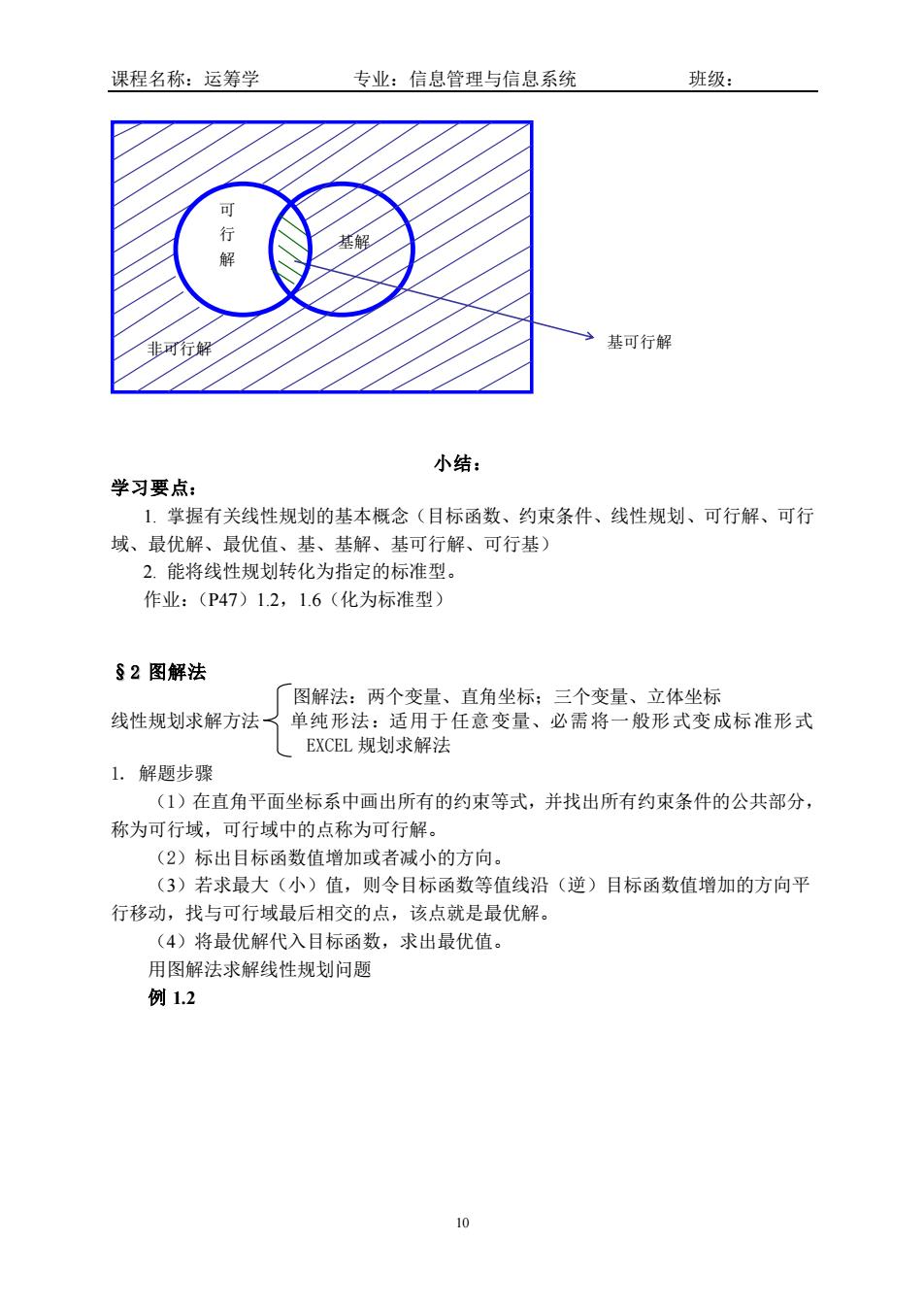
课程名称:运筹学 专业:信息管理与信息系统 班级: 基解 非行2 →基可行解 小结: 学习要点: 1.掌握有关线性规划的基本概念(目标函数、约束条件、线性规划、可行解、可行 域、最优解、最优值、基、基解、基可行解、可行基) 2.能将线性规划转化为指定的标准型。 作业:(P47)1.2,1.6(化为标准型) §2图解法 「图解法:两个变量、直角坐标:三个变量、立体坐标 线性规划求解方法了单纯形法:适用于任意变量、必需将一般形式变成标准形式 EXCEL规划求解法 1.解题步骤 (1)在直角平面坐标系中画出所有的约束等式,并找出所有约束条件的公共部分, 称为可行域,可行域中的点称为可行解。 (2)标出目标函数值增加或者减小的方向。 (3)若求最大(小)值,则令目标函数等值线沿(逆)目标函数值增加的方向平 行移动,找与可行域最后相交的点,该点就是最优解。 (4)将最优解代入目标函数,求出最优值。 用图解法求解线性规划问题 例1.2
课程名称:运筹学 专业:信息管理与信息系统 班级: 10 小结: 学习要点: 1. 掌握有关线性规划的基本概念(目标函数、约束条件、线性规划、可行解、可行 域、最优解、最优值、基、基解、基可行解、可行基) 2. 能将线性规划转化为指定的标准型。 作业:(P47)1.2,1.6(化为标准型) §2 图解法 图解法:两个变量、直角坐标;三个变量、立体坐标 线性规划求解方法 单纯形法:适用于任意变量、必需将一般形式变成标准形式 EXCEL 规划求解法 1. 解题步骤 (1)在直角平面坐标系中画出所有的约束等式,并找出所有约束条件的公共部分, 称为可行域,可行域中的点称为可行解。 (2)标出目标函数值增加或者减小的方向。 (3)若求最大(小)值,则令目标函数等值线沿(逆)目标函数值增加的方向平 行移动,找与可行域最后相交的点,该点就是最优解。 (4)将最优解代入目标函数,求出最优值。 用图解法求解线性规划问题 例 1.2 非可行解 可 行 解 基解 基可行解
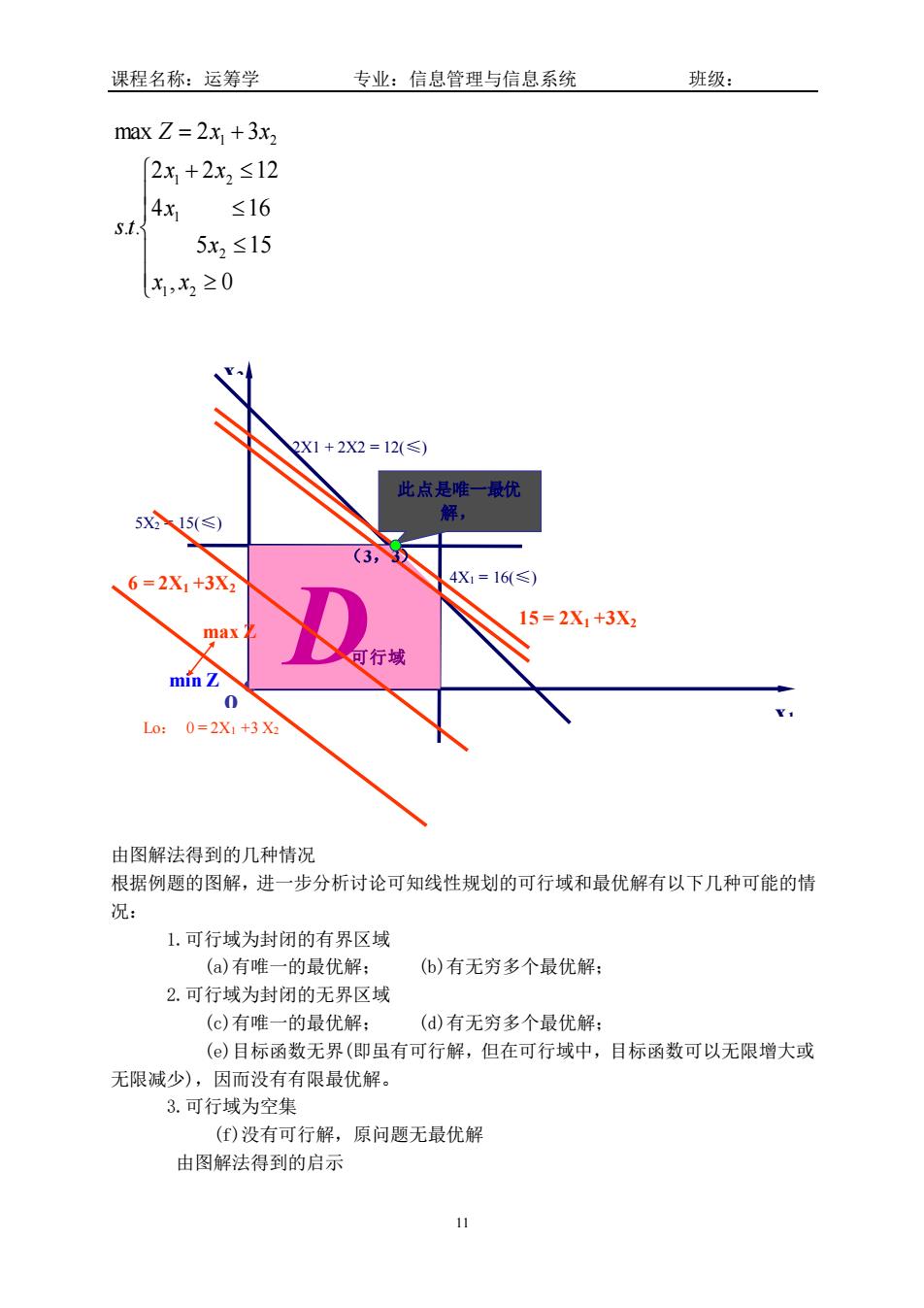
课程名称:运筹学 专业:信息管理与信息系统 班级: max Z=2x +3x, [2x+2x2≤12 4x≤16 5.4. 5x2≤15 x,2≥0 X1+2X2=12(≤) 此点是唯一最优 5Xa15(≤) (3, 6=2X1+3X 4X1=16(≤) 15=2X1+3X 可行域 min Z Lo:0=2X1+3X3 由图解祛得到的几种情况 根据例题的图解,进一步分析讨论可知线性规划的可行域和最优解有以下几种可能的情 况: 1.可行域为封闭的有界区域 (a)有唯一的最优解: (6)有无穷多个最优解: 2.可行域为封闭的无界区域 (c)有唯一的最优解: (d)有无穷多个最优解: ()目标函数无界(即虽有可行解,但在可行域中,目标函数可以无限增大或 无限减少),因而没有有限最优解。 3.可行域为空集 ()没有可行解,原问题无最优解 由图解法得到的启示
课程名称:运筹学 专业:信息管理与信息系统 班级: 11 + = + , 0 5 15 4 16 2 2 12 . . max 2 3 1 2 2 1 1 2 1 2 x x x x x x st Z x x 由图解法得到的几种情况 根据例题的图解,进一步分析讨论可知线性规划的可行域和最优解有以下几种可能的情 况: 1.可行域为封闭的有界区域 (a)有唯一的最优解; (b)有无穷多个最优解; 2.可行域为封闭的无界区域 (c)有唯一的最优解; (d)有无穷多个最优解; (e)目标函数无界(即虽有可行解,但在可行域中,目标函数可以无限增大或 无限减少),因而没有有限最优解。 3.可行域为空集 (f)没有可行解,原问题无最优解 由图解法得到的启示 x2 x1 o 2X1 + 2X2 = 12(≤) 4X1 = 16(≤) 5X2 = 15(≤) D可行域 此点是唯一最优 解, 且最优目标函数值 ( max Z=15 3,3) 6 = 2X1 +3X2 max Z 15 = 2X1 +3X2 Lo: 0 = 2X1 +3 X2 min Z

课程名称:运筹学 专业:信息管理与信息系统 班级: ()线性规划问题解的情况:唯一最优解:无穷多最优解:无界解:无可行解 (②)线性规划问题的可行域是凸集(凸多边形) (③)最优解一定是在凸集的某个顶点 (④)解题思路是,先找出凸集的任一顶点,计算其目标函数值,再与周围顶点的目 标函数值比较,如不是最大,继续比较,直到找出最大为止。 思考题 1.LP模型的可行域是否一定存在? 2.图解中如何去判断模型有唯一解、无穷多解、无界解和无可行解? 3.LP模型的可行域的顶点与什么解具有对应关系? 4你认为把所有的顶点都找出来,再通过比较目标函数值大小的方式找出最优解, 是否是最好的算法?为什么? 小结 学习要点: 1.通过图解法了解线性规划有几种解的形式 (唯一最优解:无穷多最优解:无界解:无可行解) 2.作图的关键有三点: (1)可行解区域要画正确 (2)目标函数增加的方向不能画错 (3)目标函数的直线怎样平行移动 课后作业:(P47)1.1 §3单纯形法基本原理 1、单纯形法基本原理 1.凸集和极点 2线性规划解的性质 定理1:若线性规划问题存在可行解,则该问题的可行域是凸集 定理2:线性规划问题的基可行解X对应可行域(凸集)的顶点。 定理3:若问题存在最优解,一定存在一个基可行解是最优解。(或在某个顶点取得 单纯形法的计算步骤:
课程名称:运筹学 专业:信息管理与信息系统 班级: 12 (1) 线性规划问题解的情况:唯一最优解;无穷多最优解;无界解;无可行解 (2) 线性规划问题的可行域是凸集(凸多边形) (3) 最优解一定是在凸集的某个顶点 (4) 解题思路是,先找出凸集的任一顶点,计算其目标函数值,再与周围顶点的目 标函数值比较,如不是最大,继续比较,直到找出最大为止。 思考题 1. LP 模型的可行域是否一定存在? 2. 图解中如何去判断模型有唯一解、无穷多解、无界解和无可行解? 3. LP 模型的可行域的顶点与什么解具有对应关系? 4.你认为把所有的顶点都找出来,再通过比较目标函数值大小的方式找出最优解, 是否是最好的算法?为什么? 小结 学习要点: 1. 通过图解法了解线性规划有几种解的形式 (唯一最优解;无穷多最优解;无界解;无可行解) 2. 作图的关键有三点: (1) 可行解区域要画正确 (2) 目标函数增加的方向不能画错 (3) 目标函数的直线怎样平行移动 课后作业:(P47)1.1 §3 单纯形法基本原理 1、单纯形法基本原理 1. 凸集和极点 2.线性规划解的性质 定理 1:若线性规划问题存在可行解,则该问题的可行域是凸集。 定理 2:线性规划问题的基可行解 X 对应可行域(凸集)的顶点。 定理 3:若问题存在最优解,一定存在一个基可行解是最优解。(或在某个顶点取得) 单纯形法的计算步骤:
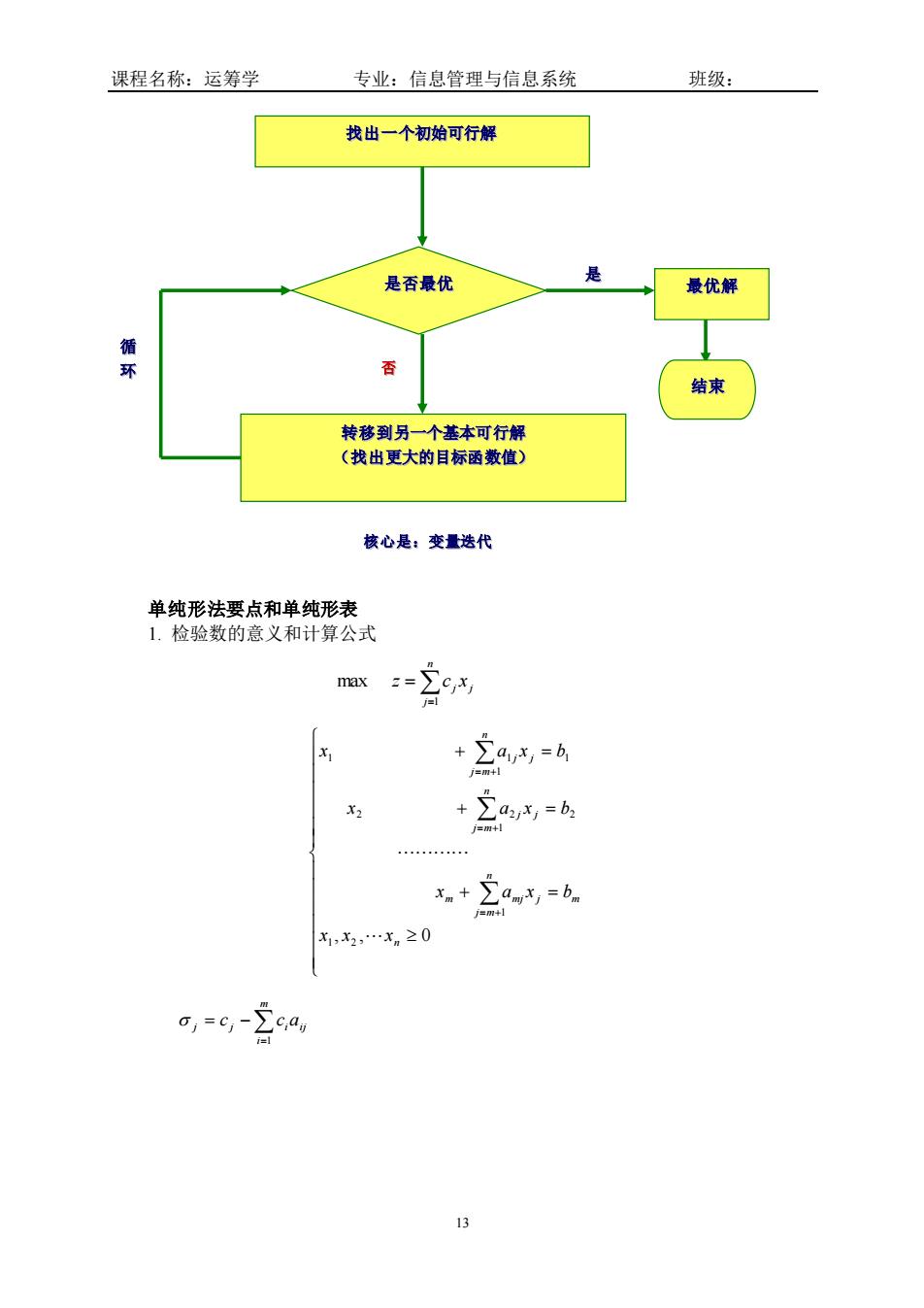
课程名称:运筹学 专业:信息管理与信息系统 班级: 找出一个初始可行解 是否最优 是 最优解 成 结束 转移到另一个基本可行解 (找出更大的目标函数值) 核心是:变量选代 单纯形法要点和单纯形表 1.检验数的意义和计算公式 mx =c +2a=4 +a=6 xa+,b. 1,.xn≥0 a,=c,-ca
课程名称:运筹学 专业:信息管理与信息系统 班级: 13 单纯形法要点和单纯形表 1. 检验数的意义和计算公式 = = n j j j z c x 1 max + = + = + = = + = + = + , , 0 1 2 1 2 1 2 2 1 1 1 1 n m n j m m mj j n j m j j n j m j j x x x x a x b x a x b x a x b = = − m i j j iaij c c 1 找出一个初始可行解 是否最优 转移到另一个基本可行解 (找出更大的目标函数值) 最优解 是 否 循 环 核心是:变量迭代 结束