课程名称:运筹学 专业:信息管理与信息系统 班级: 2.单纯形表 Ca Xa bxa Xm+l b 00 du 0 1.0 0 .1 00.0c-2cal.-ca.c-2can 3.单纯形法的基本法则 法则1最优性判定法见 法则2换入变量确定法则 设ok=max口,o,>0},则xw为换入变量。 法则3换出变量确定法则 再强调一下,这个法则的目的是,保证下一个基本解的可行性,违背这一法则,下 一个基本解一定包含负分量,即不是可行解。 法则4换基迭代运算法则 举一个简单的例子,在黑板上验算: max =2x+5x2 x1+2x2+x3 -8 5x1+2x2+x4=20 4x2 +x=12 x1,2,x3x4x320 0比 8/2 X4 20/2 4 12/4 O i 0 -1/ 2/1 14/5 01 -5/4
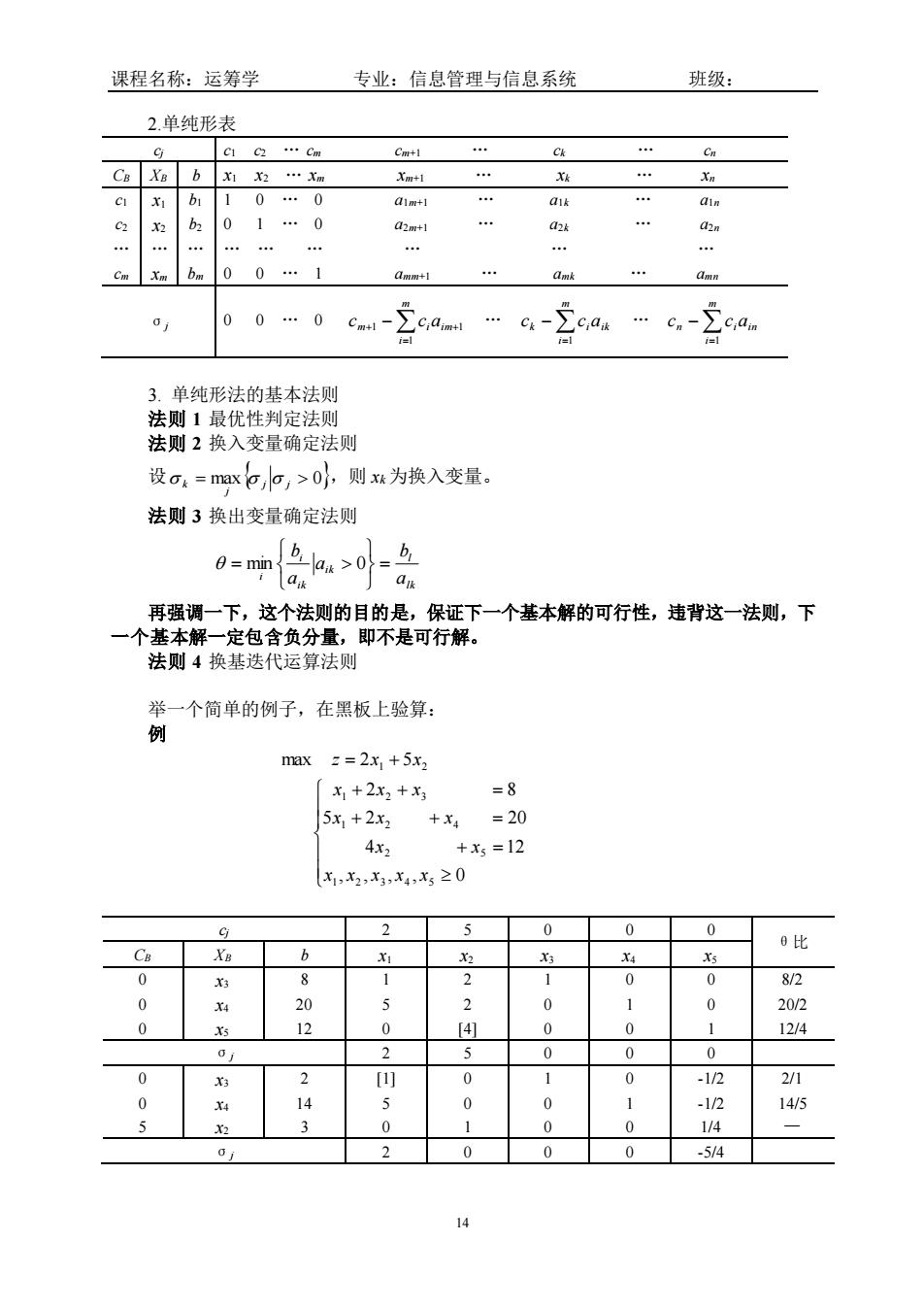
课程名称:运筹学 专业:信息管理与信息系统 班级: 14 2.单纯形表 cj c1 c2 . cm cm+1 . ck . cn CB XB b x1 x2 . xm xm+1 . xk . xn c1 c2 . cm x1 x2 . xm b1 b2 . bm 1 0 . 0 a1m+1 . a1k . a1n 0 1 . 0 a2m+1 . a2k . a2n . . . . . . 0 0 . 1 amm+1 . amk . amn σj 0 0 . 0 = + − + m i m iaim c c 1 1 1 . = − m i k iaik c c 1 . = − m i n iain c c 1 3. 单纯形法的基本法则 法则 1 最优性判定法则 法则 2 换入变量确定法则 设 = max j j 0 j k ,则 xk 为换入变量。 法则 3 换出变量确定法则 lk l ik ik i i a b a a b = = min 0 再强调一下,这个法则的目的是,保证下一个基本解的可行性,违背这一法则,下 一个基本解一定包含负分量,即不是可行解。 法则 4 换基迭代运算法则 举一个简单的例子,在黑板上验算: 例 + = + + = + + = = + , , , , 0 4 12 5 2 20 2 8 max 2 5 1 2 3 4 5 2 5 1 2 4 1 2 3 1 2 x x x x x x x x x x x x x z x x cj 2 5 0 0 0 θ比 CB XB b x1 x2 x3 x4 x5 0 0 0 x3 x4 x5 8 20 12 1 5 0 2 2 [4] 1 0 0 0 1 0 0 0 1 8/2 20/2 12/4 σj 2 5 0 0 0 0 0 5 x3 x4 x2 2 14 3 [1] 5 0 0 0 1 1 0 0 0 1 0 -1/2 -1/2 1/4 2/1 14/5 — σj 2 0 0 0 -5/4

课程名称:运筹学 专业:信息管理与信息系统 班级: -12 2 1V4 O i 00-2 -1/4 最优解X=(2,3,0,4,0)T,=2×2+5×3=19。 课堂练习:用单纯形法求解下面的线性规划 max Z =2.5x+x 3x1+5x2≤15 5.t5x1+2x2≤10 x3≥0 小结 学习要点: 1.线性规划解的概念以及3个基本定理 2.熟练学握线性规划问题的标准化 3熟练掌握单纯形法的解题思路及求解步骤 课后作业:(P47)1.3 §5单纯形法的进一步讨论一人工变量法 人工变量法: 在实际问题中有些模型并不含有单位矩阵,为了得到一组基向量和初基可行 解,在约束条件的等式左端加一组虚拟变量,得到一组基变量。这种人为加的变量 称为人工变量,构成的可行基称为人工基,用大M法或两阶段法求解,这种用人 工变量作桥梁的求解方法称为人工变量法
课程名称:运筹学 专业:信息管理与信息系统 班级: 15 2 0 5 x1 x4 x2 2 4 3 1 0 0 0 0 1 1 -5 0 0 1 0 -1/2 2 1/4 σj 0 0 -2 0 -1/4 最优解 X *=(2,3,0,4,0)T,z *=2×2+5×3=19。 课堂练习:用单纯形法求解下面的线性规划 1 2 1 2 1 2 1 2 max 2.5 3 5 15 . 5 2 10 0 Z x x x x s t x x x x = + + + 、 小结 学习要点: 1. 线性规划解的概念以及 3 个基本定理 2. 熟练掌握线性规划问题的标准化 3.熟练掌握单纯形法的解题思路及求解步骤 课后作业:(P47)1.3 §5 单纯形法的进一步讨论-人工变量法 人工变量法: 在实际问题中有些模型并不含有单位矩阵,为了得到一组基向量和初基可行 解,在约束条件的等式左端加一组虚拟变量,得到一组基变量。这种人为加的变量 称为人工变量,构成的可行基称为人工基,用大 M 法或两阶段法求解,这种用人 工变量作桥梁的求解方法称为人工变量法

课程名称:运筹学 专业:信息管理与信息系统 班级: 例1.6用大M法解下列线性规划 max Z=-3x+x x1+x2+x3≤4 -2x1+x2-x3≥1 s.1. 3x2+x3=9 x1,x2,x3≥0 解:首先将数学模型化为标准形式 max Z =-3x+ x1+X2+x3+x4=4 -2x1+x2-X3 -x3=1 3x2+x3=9 x,≥0j=12.5 系数矩阵中不存在单位矩阵,无法建立初始单纯形表。故人为添加两个单位向量,得到 人工变量单纯形法数学模型: maxZ=-3x+x -Mx-Mx x1+x2+x3+x4=4 -2x1+x2-x3-x5+x6=1 3x2+x3 +x7=9 x,20j=1,2,.,7 ”M是个很大的抽象的数不需要给出具体的数值,可以理解为它能大于 一个确定数值:再用前面介绍的单纯形法求解该模型,计算结果见下表。 .3 -M -M 0 -M 0 00 1 3 2M M 1
课程名称:运筹学 专业:信息管理与信息系统 班级: 16 例 1.6 用大 M 法解下列线性规划 + = − + − + + = − + , , 0 3 9 2 1 4 . . max 3 1 2 3 2 3 1 2 3 1 2 3 1 3 x x x x x x x x x x x st Z x x 解:首先将数学模型化为标准形式 = + = − + − − = + + + = = − + 0, 1,2, ,5 3 9 2 1 4 max 3 2 3 1 2 3 5 1 2 3 4 1 3 x j x x x x x x x x x x Z x x j 系数矩阵中不存在单位矩阵,无法建立初始单纯形表。故人为添加两个单位向量,得到 人工变量单纯形法数学模型: = + + = − + − − + = + + + = = − + − − 0, 1,2, ,7 3 9 2 1 4 max 3 2 3 7 1 2 3 5 6 1 2 3 4 1 3 6 7 x j x x x x x x x x x x x x Z x x Mx Mx j 其中:M 是一个很大的抽象的数,不需要给出具体的数值,可以理解为它能大于给定的 任何一个确定数值;再用前面介绍的单纯形法求解该模型,计算结果见下表。 cj -3 0 1 0 0 -M -M CB XB b x1 x2 x3 x4 x5 x6 x7 θi 0 x4 4 1 1 1 1 0 0 0 4 -M x6 1 -2 (1) -1 0 -1 1 0 1 -M x7 9 0 3 1 0 0 0 1 3 j -3-2M 4M 1 0 -M 0 0 0 x4 3 3 0 2 1 1 -1 0 1 0 x2 1 -2 1 -1 0 -1 1 0 —

课程名称:运筹学 专业:信息管理与信息系统 班级: -Mx7 6 M-3 M+1 M 0 x4 2 x2 3 1/3 0 13 9 012/3)0 12.121632 3/2 -M-3/ 1/2-M 0 x40 0 0 0 1 -1/21/2 -1/2 0 0 0 332 34.34 14 -9/2 0 0 0 -3/43/4-M -1/4-M 0 解的判别(Max型): 1)唯一最优解判别:最优表中所有非基变量的检验数非零,则线性规划具有唯一最优解。 2)无穷多最优解判别:最优表中存在非基变量的检验数为零,则线则性规划具有多重最 优解(或多重最优解) 3)无界解判别:某个ok>0且aik≤0(i=1,2,.,m)则线性规划具有无界解。 4)无可行解的判断:当用大M单纯形法计算得到最优解并且存在人工变量在基,且不 为0时,表明原问题无可行解。 5)退化解的判别:存在某个基变量为零的基本可行解。 小结 学习要点: 1.掌握人工变量法一大M法 2。能准确根据单纯形表中的检验数判别所解问题的解的类型 课后作业:(P48)1.6(列初始单纯形表),1.7(a)(大M法) §7线性规划模型的应用及举例 常见问题 合理利用限材问题:如何下料使用材最少。 配料问题:在原料供应量的限制下如何获取最大利润。 投资问题:从投资项目中选取方案,使投资回报最大。 产品生产计划:合理利用人力、物力、财力等,使获利最大。 劳动力安排:用最少的劳动力来满足工作的需要 运输问题:如何制定调运方案,使总运费最小。 例1.13某糖果厂用原料A、B、C加工成不同牌号的糖果甲、乙、丙。有关参数如 下表所示,问该厂每月生产这三种各多少千克,使该厂获利最大。 试建立该问题的线性规划模型。 17
课程名称:运筹学 专业:信息管理与信息系统 班级: 17 -M x7 6 (6) 0 4 0 3 -3 1 1 j 6M-3 0 4M+1 0 3M -4M 0 0 x4 0 0 0 0 1 -1/2 1/2 -1/2 — 0 x2 3 0 1 1/3 0 0 0 1/3 9 -3 x1 1 1 0 (2/3) 0 1/2 -1/2 1/6 3/2 j 0 0 3 0 3/2 -M-3/ 2 1/2-M 0 x4 0 0 0 0 1 -1/2 1/2 -1/2 0 x2 1 -2 1 0 0 -1 1 0 1 x3 3/2 3/2 0 1 0 3/4 -3/4 1/4 j -9/2 0 0 0 -3/4 3/4-M -1/4-M 解的判别(Max 型): : 1)唯一最优解判别:最优表中所有非基变量的检验数非零,则线性规划具有唯一最优解。 2)无穷多最优解判别:最优表中存在非基变量的检验数为零,则线则性规划具有多重最 优解(或多重最优解)。 3)无界解判别:某个σk>0 且 aik≤0(i=1,2,.,m)则线性规划具有无界解。 4)无可行解的判断:当用大 M 单纯形法计算得到最优解并且存在人工变量在基,且不 为 0 时,表明原问题无可行解。 5)退化解的判别:存在某个基变量为零的基本可行解。 小结 学习要点: 1. 掌握人工变量法—大 M 法 2. 能准确根据单纯形表中的检验数判别所解问题的解的类型 课后作业:(P48) 1.6 (列初始单纯形表) , 1.7(a)(大 M 法) §7 线性规划模型的应用及举例 常见问题 合理利用限材问题:如何下料使用材最少。 配料问题:在原料供应量的限制下如何获取最大利润。 投资问题:从投资项目中选取方案,使投资回报最大。 产品生产计划:合理利用人力、物力、财力等,使获利最大。 劳动力安排:用最少的劳动力来满足工作的需要。 运输问题:如何制定调运方案,使总运费最小。 例 1.13 某糖果厂用原料 A、B、C 加工成不同牌号的糖果甲、乙、丙。有关参数如 下表所示,问该厂每月生产这三种各多少千克,使该厂获利最大。 试建立该问题的线性规划模型

课程名称:运筹学 专业:信息管理与信息系统 班级: 甲 丙 原料成本(元每月限制用 /kg) 量(kg A ≥60% ≥30% 2000 B 1.5 2500 <200% ≤500% ≤600% 1200 加工费(元 05 0.4 0.3 /kg) 售价(元kg)34 2.852.25 其中,百分数表示各糖果中各原料的含量 解:设刘表示生产第j种糖果使用的第1种原料的质量,则 MaxZ=(3.4-0.5)×x11+x21+x31)+(2.85-0.4)×(x12+x22+x32)+(2.25-0.3)× (x13+x23+33)2×(X11+x12+x13)-1.5×(21+x22+x231×(31+W32+33 st.x11+x12+x13≤2000 X21+X22+X23≤2500 X31+x32+x33≤1200 x11≥0.6(x11tx21+X31) X31≤0.2(x11+x21+x31) X12≥0.3(x12+x22+x32) X32≤0.5(x12tx22+x32) X33≤0.6(x13+x23+X33) 对≥0(1,2,3:j户1,2,3) 学习要点: 1.能准确地将所论的实际问题用相应的线性规划的数学模型表示出来 课后作业:(P49)1.13,1.14
课程名称:运筹学 专业:信息管理与信息系统 班级: 18 甲 乙 丙 原料成本(元 /kg) 每月限制用 量(kg) A ≥60% ≥30% 2 2000 B 1.5 2500 C ≤ 20% ≤ 50% ≤ 60% 1 1200 加工费(元 /kg) 0.5 0.4 0.3 售价(元/kg) 3.4 2.85 2.25 其中,百分数表示各糖果中各原料的含量 解:设 xij 表示生产第 j 种糖果使用的第 i 种原料的质量,则 Max Z=(3.4-0.5)× (x11+x21+ x31) +(2.85-0.4)×(x12+x22+ x32) +(2.25-0.3)× (x13+x23+x33)-2×(x11+x12+x13)-1.5×(x21+x22+x23)-1×(x31+x32+x33) s.t. x11+x12+x13 ≤2000 x21+x22+x23 ≤2500 x31+x32+x33≤1200 x11≥0.6(x11+x21+ x31) x31 ≤ 0.2(x11+x21+ x31) x12≥0.3(x12+x22+ x32) x32 ≤ 0.5(x12+x22+ x32) x33 ≤ 0.6(x13+x23+ x33) xij≥0 (i=1,2,3;j=1,2,3) 学习要点: 1. 能准确地将所论的实际问题用相应的线性规划的数学模型表示出来 课后作业:(P49) 1.13,1.14