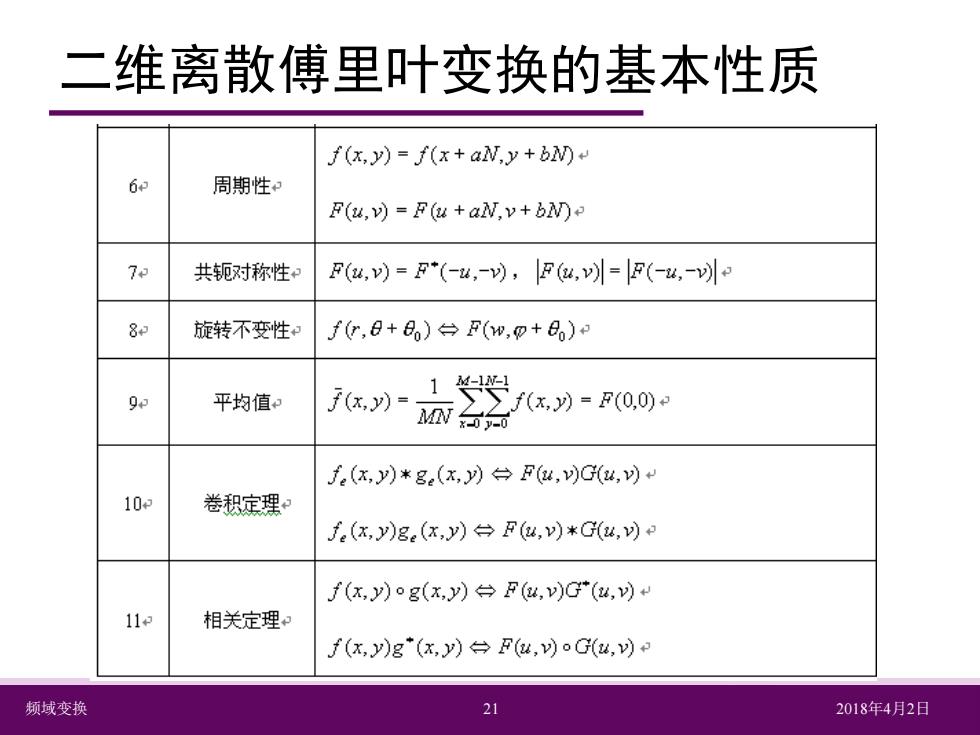
二维离散傅里叶变换的基本性质 f(x,y)=f(x+aN,y+bN) 62 周期性 F(u,)=F(u+aW,v+bWD和 7 共轭对称性 F(u,)=F*(-4,-),F(u,=F(-4,- 8 旋转不变性 f〔,8+月)台F(w,p+)r (x,)= 1- 93 平均值 MN7-0 f(x,)=F(0,0)+ f(x,y)*ge(x,月台Fu,)G(u,)+ 102 卷积定理 f(x,y)ge(x,y)台F(w,)*G(4,)日 f(x,y))g(x,y)台F(4,)G(,) 11 相关定理 f(x,y)g(x,y)F(u,v)oG(u,v) 频域变换 21 2018年4月2日
频域变换 21 2018年4月2日 二维离散傅里叶变换的基本性质

基本性质 设二维离散函数为f1(x,y)和f2(x,y),它们所对应的傅里叶 变换分别为F1(u,v)和F2(u,)。 ·线性性质 ●af1(x,y)+bf2(x,y)台aF1(u,v)+bF2(u,v) 式中,a,b为常数。 此性质可以节约求傅里叶变换的时间。若已经得到了f,(x,y) 和f2(x,y)及F1(u,v)和F2(u,v)的值,则af1(x,y)+bf2(x,y) 的傅里叶变换只要求得aF1(u,v)+bF,(u,v)就可以了。 频域变换 22 2018年4月2日
频域变换 22 2018年4月2日 基本性质 设二维离散函数为𝑓𝑓1(𝑥𝑥, 𝑦𝑦)和𝑓𝑓2(𝑥𝑥, 𝑦𝑦),它们所对应的傅里叶 变换分别为𝐹𝐹1(𝑢𝑢, 𝑣𝑣)和𝐹𝐹2(𝑢𝑢, 𝑣𝑣)。 线性性质 𝑎𝑎𝑓𝑓1 𝑥𝑥, 𝑦𝑦 + 𝑏𝑏𝑓𝑓2 𝑥𝑥, 𝑦𝑦 ⟺ 𝑎𝑎𝐹𝐹1 𝑢𝑢, 𝑣𝑣 + 𝑏𝑏𝐹𝐹2 𝑢𝑢, 𝑣𝑣 式中,𝑎𝑎, 𝑏𝑏为常数。 此性质可以节约求傅里叶变换的时间。若已经得到了𝑓𝑓1(𝑥𝑥, 𝑦𝑦) 和𝑓𝑓2(𝑥𝑥, 𝑦𝑦)及𝐹𝐹1(𝑢𝑢, 𝑣𝑣)和𝐹𝐹2(𝑢𝑢, 𝑣𝑣)的值,则𝑎𝑎 𝑓𝑓1(𝑥𝑥, 𝑦𝑦) + 𝑏𝑏𝑏𝑏2(𝑥𝑥, 𝑦𝑦) 的傅里叶变换只要求得𝑎𝑎𝑎𝑎1(𝑢𝑢, 𝑣𝑣) + 𝑏𝑏𝑏𝑏2(𝑢𝑢, 𝑣𝑣) 就可以了

基本性质 ·比例性质 。对于两个标量a和b,有 faxF台) 上式说明了在空间比例尺度的展宽,相应于频域比例尺度的 压缩,其幅值也减少为原来的1/八abl,如图所示。 (a)比例尺度展宽前的频谱 (b)比例尺度展宽后的烦谱 频域变换 33 2018年4月2日
频域变换 23 2018年4月2日 基本性质 比例性质 对于两个标量𝑎𝑎和𝑏𝑏,有 𝑓𝑓(𝑎𝑎𝑎𝑎, 𝑏𝑏𝑏𝑏)⟺ 1 |𝑎𝑎𝑎𝑎| 𝐹𝐹 𝑢𝑢 𝑎𝑎 , 𝑣𝑣 𝑏𝑏 上式说明了在空间比例尺度的展宽,相应于频域比例尺度的 压缩,其幅值也减少为原来的1/|𝑎𝑎𝑎𝑎|,如图所示

基本性质 ·可分离性 M-1 W-1 F(u,v)= MN M-1「N- f(x,y)= ∑F,ea u=0 利用这个性质,一个二维离散傅里叶变换(或逆变换)可 通过进行两次一维离散傅里叶变换(或逆变换)来完成。 频域变换 24 2018年4月2日
频域变换 24 2018年4月2日 基本性质 可分离性 利用这个性质,一个二维离散傅里叶变换(或逆变换)可 通过进行两次一维离散傅里叶变换(或逆变换)来完成

可分离性 例如,以正变换为例, 先对f(x,y)沿y轴进行傅里叶变换得到F(x,), N /(x. FE)= N-1 v=0 再沿着x轴对F(x,)进行一维离散傅里叶变换,得到F(u,v) F()=e M x=0 显然对f(x,y)先沿x轴进行离散傅里叶变换,再沿y轴进行离 散傅里叶变换结果一样。逆变换也是如此。 频域变换 25 2018年4月2日
频域变换 25 2018年4月2日 可分离性 例如,以正变换为例, 先对𝑓𝑓(𝑥𝑥, 𝑦𝑦)沿𝑦𝑦轴进行傅里叶变换得到𝐹𝐹(𝑥𝑥, 𝑣𝑣), 再沿着x轴对𝐹𝐹(𝑥𝑥, 𝑣𝑣)进行一维离散傅里叶变换,得到𝐹𝐹(𝑢𝑢, 𝑣𝑣) 显然对𝑓𝑓(𝑥𝑥, 𝑦𝑦)先沿𝑥𝑥轴进行离散傅里叶变换,再沿𝑦𝑦轴进行离 散傅里叶变换结果一样。逆变换也是如此。 ∑ − = − = 1 0 2 ( , ) 1 ( , ) N y j vy N f x y e N F x v π ∑ − = − = 1 0 2 ( , ) 1 ( , ) M x j ux M F x v e M F u v π