可分离性 。先对f(x,y)按行进行傅里叶变换得到F(x,),再对 F(x,)按列进行傅里叶变换,便可得到f(x,y)的傅 里叶变换结果。 f(x,y) F(c,习 F(u,) 按行进行一维DFT 按列进行一维DFT 频域变换 26 2018年4月2日
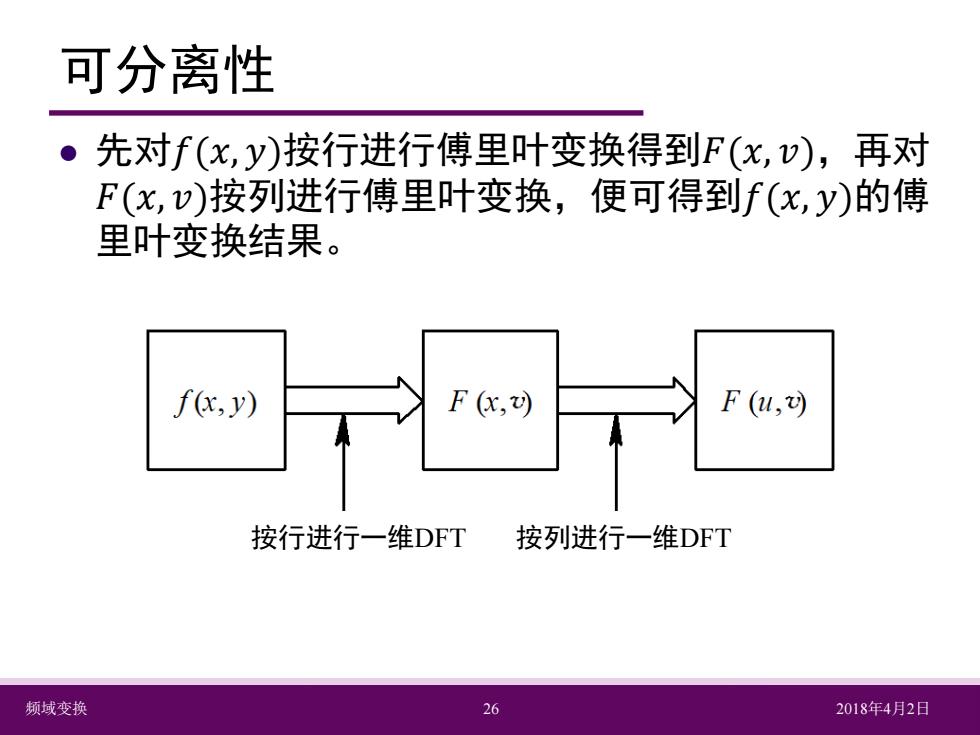
频域变换 26 2018年4月2日 可分离性 先对𝑓𝑓(𝑥𝑥, 𝑦𝑦)按行进行傅里叶变换得到𝐹𝐹(𝑥𝑥, 𝑣𝑣),再对 𝐹𝐹(𝑥𝑥, 𝑣𝑣)按列进行傅里叶变换,便可得到𝑓𝑓(𝑥𝑥, 𝑦𝑦)的傅 里叶变换结果。 按行进行一维DFT 按列进行一维DFT

基本性质 。频率位移及空间位移 频率位移:f(x,y)e2M+wW台F(u-4o,y-vo)》 空间位移:f(x-x,y-yo)台F(u,)e2a,/M+ 这一性质表明,当用ei2πuox/M+voy/)乘以f(x,y),求乘积的傅里 叶变换,可以使空间频率域u,v平面坐标系的原点从(0,0)平移到 (uo,o)的位置;同样,当用e-j2π(uox/M+voy/乘以F(u,),并求 此乘积的离散傅里叶反变换,可以使空间x,y平面坐标系原点从 (0,0)平移到(xo,yo)的位置。 频域变换 27 2018年4月2日
频域变换 27 2018年4月2日 基本性质 频率位移及空间位移 频率位移: ( , ) ( , ) 0 0 2 ( ) 0 0 f x y e F u u v v j u x M v y N ⇔ − − π + 空间位移: 2 ( ) 0 0 0 0 ( , ) ( , ) j ux M vy N f x x y y F u v e ⇔ − + − − π 这一性质表明,当用𝑒𝑒𝑗𝑗𝑗𝑗𝑗(𝑢𝑢0𝑥𝑥/𝑀𝑀+𝑣𝑣0𝑦𝑦/𝑁𝑁) 乘以 𝑓𝑓(𝑥𝑥, 𝑦𝑦),求乘积的傅里 叶变换,可以使空间频率域𝑢𝑢, 𝑣𝑣平面坐标系的原点从(0,0)平移到 (𝑢𝑢0, 𝑣𝑣0)的位置;同样,当用𝑒𝑒−𝑗𝑗𝑗𝑗𝑗(𝑢𝑢0𝑥𝑥/𝑀𝑀+𝑣𝑣0𝑦𝑦/𝑁𝑁) 乘以𝐹𝐹(𝑢𝑢, 𝑣𝑣),并求 此乘积的离散傅里叶反变换,可以使空间𝑥𝑥, 𝑦𝑦平面坐标系原点从 (0,0)平移到(𝑥𝑥0, 𝑦𝑦0)的位置

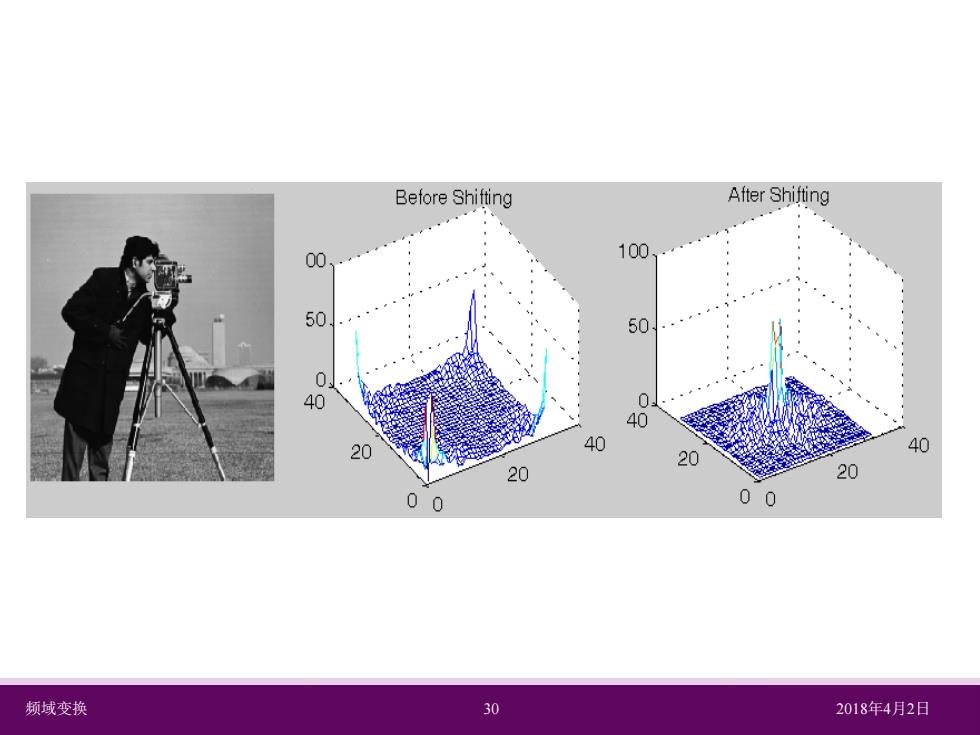
频率位移及空间位移 在数字图像处理中,为了清楚地分析图像傅里叶谱的分布情 况,经常需要把空间频率平面坐标系的原点移到(M/2,N/2) 的位置,即令uo=M/2vo=N/2,则 上式表明:如果需要将图像频谱的原点从起始点(0,0)移到图 像的中心点(M/2,N/2),只要f(x,y)乘上(-1)x+y因子进行 傅里叶变换即可实现。 频域变换 28 2018年4月2日
频域变换 28 2018年4月2日 频率位移及空间位移 在数字图像处理中,为了清楚地分析图像傅里叶谱的分布情 况,经常需要把空间频率平面坐标系的原点移到(𝑀𝑀/2, 𝑁𝑁/2) 的位置,即令𝑢𝑢0 = 𝑀𝑀/2 𝑣𝑣0 = 𝑁𝑁/2,则 上式表明:如果需要将图像频谱的原点从起始点(0,0)移到图 像的中心点(𝑀𝑀/2, 𝑁𝑁/2) ,只要𝑓𝑓(𝑥𝑥, 𝑦𝑦)乘上 −1 𝑥𝑥+𝑦𝑦因子进行 傅里叶变换即可实现。 − ⇔ − − + 2 , 2 ( , )( 1) N v M f x y F u x y

6 频域变换 29 2018年4月2日
频域变换 29 2018年4月2日 (a) (b) (c)
Before Shifting After Shifting 00 100 50 50 0 40 0 40 20 40 40 20 20 20 00 00 频域变换 30 2018年4月2日
频域变换 30 2018年4月2日