
离散函数的傅里叶变换 由欧拉公式可知 eio =cos0+jsine 将上式代入,并利用cos(-)=cos(),可得 r=2eea2-sm2 可见,离散序列的傅里叶变换仍是一个离散的序列,每一 个u对应的傅里叶变换结果是所有输入序列f(x)的加权和 (每一个(x)都乘以不同频率的正弦和余弦值),决定 了每个傅里叶变换结果的频率。 频域变换 16 2018年4月2日
频域变换 16 2018年4月2日 由欧拉公式可知 将上式代入,并利用cos(-𝜃𝜃) = cos(𝜃𝜃),可得 离散函数的傅里叶变换 θ θ θ e cos jsin j = + ∑ − = = − 1 0 2 sin 2 ( ) ( ) cos N x N ux j N ux F u f x π π 可见,离散序列的傅里叶变换仍是一个离散的序列,每一 个𝑢𝑢对应的傅里叶变换结果是所有输入序列𝑓𝑓(𝑥𝑥)的加权和 (每一个𝑓𝑓(𝑥𝑥)都乘以不同频率的正弦和余弦值),𝑢𝑢决定 了每个傅里叶变换结果的频率

离散函数的傅里叶变换 。一维离散傅里叶变换的复数形式、指数形式、振幅、相角 以及能量谱的表示类似一维连续函数的相应的表达式 ·将一维离散傅里叶变换推广到二维,则二维离散傅里叶变 换对定义为: /x,=u)=∑fx,e M-1N- 27* MN x=0y=0 FF明=fcy-览2Fu,e ✉7 v=0 ·类似一维离散傅里叶变换,系数1/MN可以在正变换或逆变换中,也可以在 正变换和逆变换前分别乘以系数,只要两式系数的乘积等于1/MN即可。 二维离散函数的复数形式、指数形式、振幅、相角、能量谱的表示类似二维 连续函数的相应的表达式。 频域变换 17 2018年4月2日
频域变换 17 2018年4月2日 一维离散傅里叶变换的复数形式、指数形式、振幅、相角 以及能量谱的表示类似一维连续函数的相应的表达式 将一维离散傅里叶变换推广到二维,则二维离散傅里叶变 换对定义为: 离散函数的傅里叶变换 2 ( ) 1 0 1 0 1 2 ( ) 1 0 1 0 [ ( , )] ( , ) ( , ) ( , ) 1 [ ( , )] ( , ) N vy M ux j N v M u N vy M ux M j x N y F F u v f x y F u v e f x y e MN F f x y F u v + − = − = − − + − = − = ∑ ∑ ∑∑ = = = = π π 类似一维离散傅里叶变换,系数1/𝑀𝑀𝑀𝑀可以在正变换或逆变换中,也可以在 正变换和逆变换前分别乘以系数,只要两式系数的乘积等于1/𝑀𝑀𝑀𝑀即可。 二维离散函数的复数形式、指数形式、振幅、相角、能量谱的表示类似二维 连续函数的相应的表达式

频域变换 18 2018年4月2日
频域变换 18 2018年4月2日

频域变换 19 2018年4月2日
频域变换 19 2018年4月2日
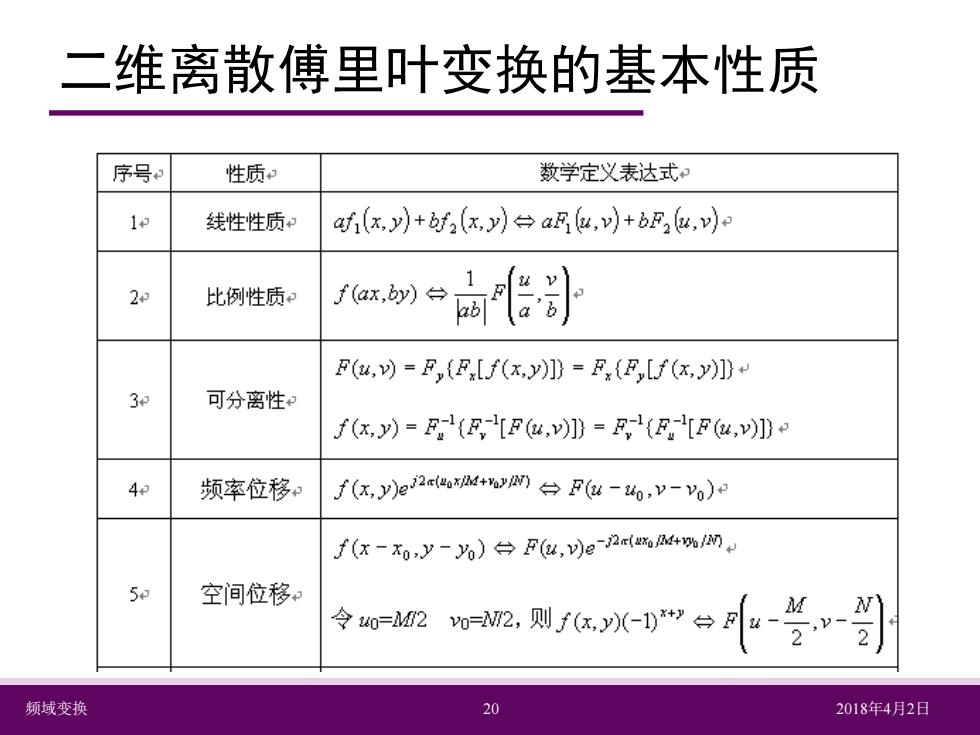
二维离散傅里叶变换的基本性质 序号 性质 数学定义表达式 1 线性性质 af (x.y)+bf(x.y)an(u.v)+bF(u.v)o 2 此例性质。 f(ax,y)f F(u.v)=F,(F,[f(x,y)1)=F,(F,[f (xy)]) 3 可分离性 f(x,y)=F(R,[Fu,]》=耳,(E[Fu,]》P 4 频率位移。 f(xy)eF(u-vo) f(x-x0y-6)台F6u,)g2(44%m 5e 空间位移。 频域变换 20 2018年4月2日
频域变换 20 2018年4月2日 二维离散傅里叶变换的基本性质