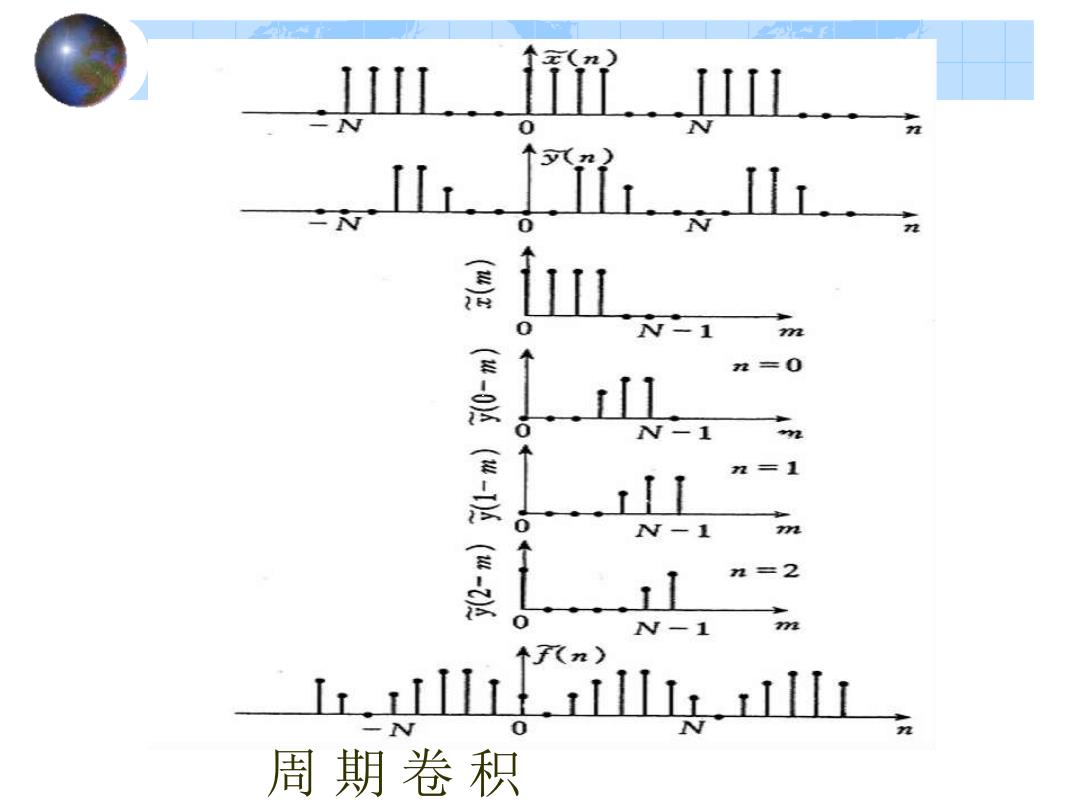
(n) JII li N (n) 72 是 0 N-1 m =0 (1(岁10 N-1 n=1 -1 ”2 N-1 个fn) 111 0 周期卷积
周 期 卷 积
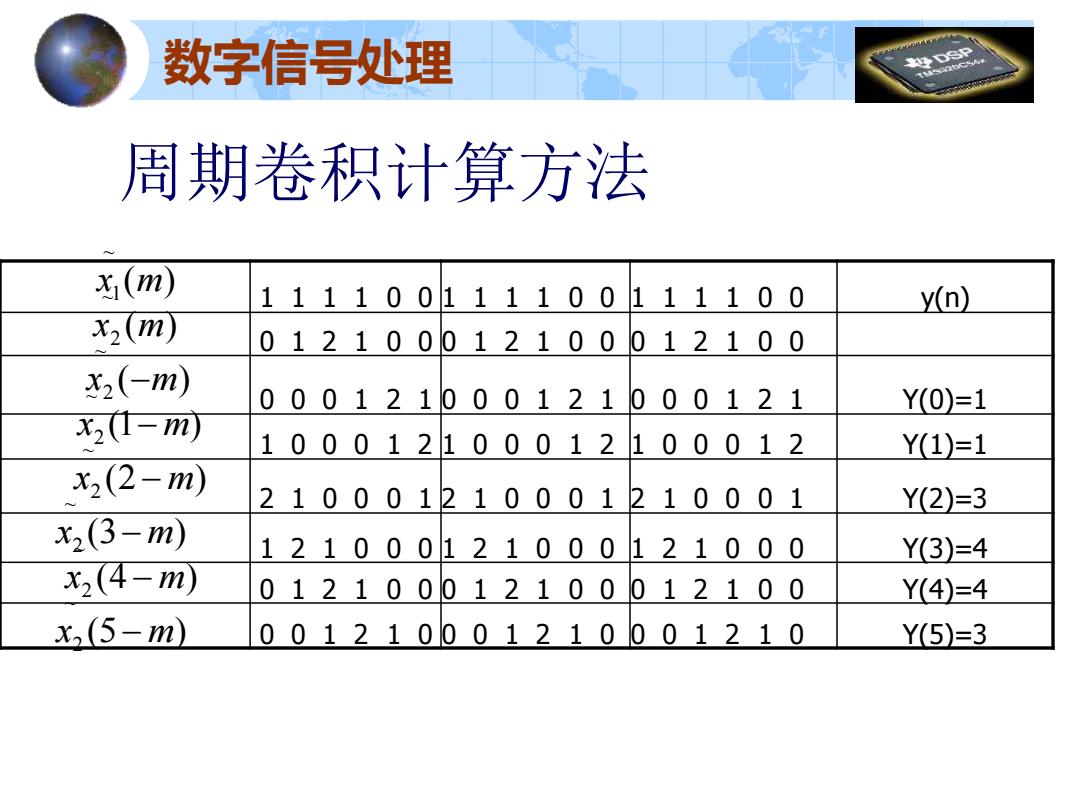
数字信号处理 9o9 周期卷积计算方法 (m) 111100111100111100 y(n) x2(m)】 012100012100012100 x2(-m) 000121000121000121 Y(0)=1 x21-m) 100012100012100012 Y(1)=1 x2(2-m) 210001210001210001 Y(2)=3 x2(3-m) 121000121000121000 Y(3)=4 x2(4-m 012100012100012100 Y(4)=4 x2(5-m) 001210001210001210 Y(5)=3
1 1 1 1 0 0 1 1 1 1 0 0 1 1 1 1 0 0 y(n) 0 1 2 1 0 0 0 1 2 1 0 0 0 1 2 1 0 0 0 0 0 1 2 1 0 0 0 1 2 1 0 0 0 1 2 1 Y(0)=1 1 0 0 0 1 2 1 0 0 0 1 2 1 0 0 0 1 2 Y(1)=1 2 1 0 0 0 1 2 1 0 0 0 1 2 1 0 0 0 1 Y(2)=3 1 2 1 0 0 0 1 2 1 0 0 0 1 2 1 0 0 0 Y(3)=4 0 1 2 1 0 0 0 1 2 1 0 0 0 1 2 1 0 0 Y(4)=4 0 0 1 2 1 0 0 0 1 2 1 0 0 0 1 2 1 0 Y(5)=3 ( ) ~ x1 m ( ) ~ x2 m ( ) ~ x2 −m (1 ) ~ x2 − m (2 ) ~ x2 − m (3 ) ~ x2 − m (4 ) ~ x2 − m (5 ) ~ x2 − m 周期卷积计算方法 数字信号处理
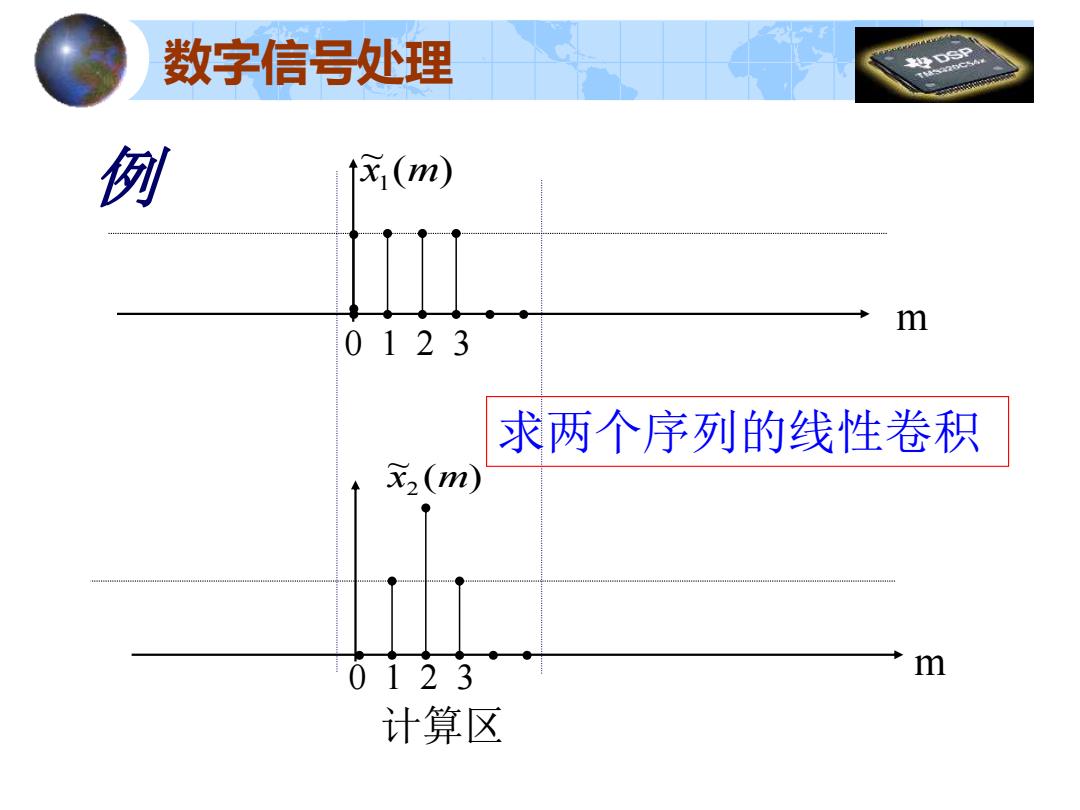
数字信号处理 DSP 例 ↑区(m) m 0123 求两个序列的线性卷积 x2(m) 0123 m 计算区
例 ( ) ~ x2 m m 计算区 m ( ) ~ x1 m 0 1 2 3 数字信号处理 求两个序列的线性卷积 0 1 2 3
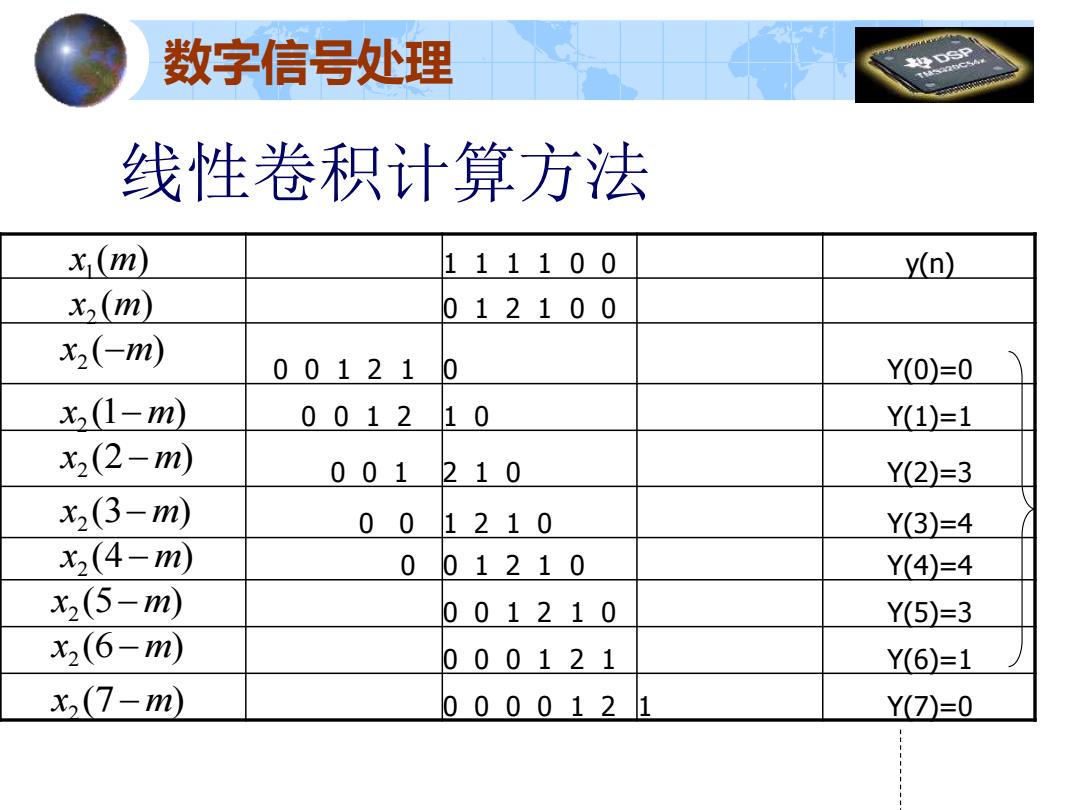
数字信号处理 9 线性卷积计算方法 x(m) 111100 yn】 x,(m) 012100 x2(-m) 001210 Y(0)=0 x,(1-m) 0012 10 Y(1)=1 x2(2-m) 001 210 Y(2)=3 x2(3-m) 00 1210 Y3)=4 x2(4-m) 0 01210 Y(4)=4 x2(5-m) 001210 Y(5)=3 x2(6-m) 000121 Y(6)=1 x,(7-m) 0000121 Y(7)=0
1 1 1 1 0 0 y(n) 0 1 2 1 0 0 0 0 1 2 1 0 Y(0)=0 0 0 1 2 1 0 Y(1)=1 0 0 1 2 1 0 Y(2)=3 0 0 1 2 1 0 Y(3)=4 0 0 1 2 1 0 Y(4)=4 0 0 1 2 1 0 Y(5)=3 0 0 0 1 2 1 Y(6)=1 0 0 0 0 1 2 1 Y(7)=0 线性卷积计算方法 数字信号处理 ( ) x1 m ( ) x2 m ( ) x2 −m (1 ) x2 −m (2 ) x2 −m (3 ) x2 −m (4 ) x2 −m (5 ) x2 −m (6 ) x2 −m (7 ) x2 −m

数字信号处理 经9 2.1.2离散傅里叶变换DFT 一.预备知识 1.余数运算表达式 如果n=n,+mW 0≤n≤W-1 m为整数;则有: (n)x=(n1) 此运算符表示n被N除,商为m,余数为n (n)是(《n)的解,或称作取余数,或说作n对 N取模值,或简称为取模值,n模N
2.1.2离散傅里叶变换DFT 一.预备知识 1.余数运算表达式 如果 , m为整数;则有: 此运算符表示n被N除,商为m,余数为 。 是 的解,或称作取余数,或说作n对 N取模值, 或简称为取模值,n模N。 n = n1 + mN 0 1 n1 N − (( )) ( ) n N = n1 1 n ( )1 n (( ))N n 数字信号处理