
第三章功和热量 ,27◆ 与单位质量相关联的功记为: ws m (3.1) 最后一个总的说明是功与系统的选择有关。注意到在图3-2中,如果()图的系统包括 全部的电池-电阻装置,(b)图的系统包括全部的电池-电机-滑轮-重物装置的话,则没有能量 穿越系统边界,也就没有作功。对系统的选取对于确定功是非常重要的。 3.3由移动边界引起的准平衡功 在不同的工程情况下功有多种模式。其中包括拉紧绳子所需要的功、旋转轴所需要的功、 克服摩擦移动所需要的功、导致电流流过电阻所需要的功、以及向电容器充电所需要的功。还 有许多功的模式包含在其他的过程中。在本书中,我们主要涉及用来克服压力以使边界移动 所需要的功。 考虑如图3-3所示的活塞气缸装置。密封装置使气体保存在气缸里。整个气缸内的压 力均匀相等,而且不受重力、磁场或电场的影响。这确保了准平衡过程的实现,在准平衡过程 中假定气体经历了一系列平衡状态。现在,允许活塞向上移动一小段距离d,从而使气体膨 胀。作用在活塞上的总的力等于压力乘以活塞的面积。该压力是以绝对压力表达的,因为压 力是分子运动的结果;任何一个分子的运动都会产生压力,从而在边界移动时作功。系统(气 体)作用于外界(活塞)的微元功是力与距离的乘积: ow=PAdl (3.2) 气体 气体 图3-3 我们来简略地讨论一下符号W。Adl就是微分容积dV,式(3.2)可以写成如下形式: 8W PdV (3.3) 当活塞从某-一位置到另一位置12,上述表达式可以积分为 w pav (3.4) 这里我们假设,在活塞从容积V到容积Vz的移动过程巾,任意位置的压力都是已知的。典 型的压力-容积图见图3-4。功W:2是PV曲线下的面积。 考虑积分过程,这里强调式(3.4)中的两个非常重要的特性。第一点,当我们从状态①到 状态②时,代表功的这部分面积极其依赖于我们所遵循的路径。就是说,在图3-4(a)中的状 态①和②与(b)中的是相同的,然而在PV曲线下的面积却非常不同。除了取决于这两个端 点之外,功还取决于连接这两个端点的实际的路径。所以,与点函数相对,功是一个路径函数, 点函数仅取决于端点。路径函数的微分叫做不精确微分,相反的,点函数的微分是精确微分。 不精确微分用符号8表示。W的积分是W:-2,这里的下标强调功是与从状态①到状态②所 经历的路径相联系的。不过,该下标是可以省略的,可以将所作功简单写成W。我们从来不 会写成W:或W,因为功并非与状态而是与过程相联系。功不是性质。一个精确微分(如 dT)的积分是

·28· 工程热力学 (dT=Te-T (3.5) 其中T1是状态①下的温度,T2是状态②下的温度。 ① ② (a) (b 图3-4 从式(3.4)中可以看到的第二点是,在任意一个中间位置,整个容积内的出力保持恒定。 该系统经历了如图3-4的PV图中所示的每一个平衡状态。即使变量看起来变化非常快, 也经常被假定为平衡状态。燃烧是非常快速的过程,它不能被看作是准平衡过程。内燃机中 的其他过程(膨胀,排气,吸入,以及压缩)都可以被假定为准平衡过程,它们以热力学上较慢的 速率进行着。 作为对功的最后一个说明,我们现在可以讨论一下第一章定义的简单系统的意义是什么。 对于一个不受表面效应、磁场和电场影响的系统,功的模式仅仅是由于作用在移动边界上的压 力造成的。对于这样一个简单的系统只要两个独立变量就可以确立由均匀物质组成的系统的 一个平衡状态。如果有其他模式的功存在,比如由于电场而产生的功,则需要增加独立变量, 如电场强度。 例3.11kg千度为20%的水蒸气在200kPa的定压下加热,直至温度达到400℃。计算水蒸 气所作的功, 解国功可由下式得出 W =PdV P(V:-Vi)=mP(t-) 为了计算功就必须确定功和?。由表C-2可得 4=y+x(w-y)=0.001061+(0.2)(0.8857-0.001061)=0.1780(m/kg) 由过热蒸汽表,根据T2=400℃和Pz=0.2MPa,我们可以确定状态②: 边=1.549m/kg 则功为 W=(1)(200)(1.549-0.1780)=274.2(k) 注意:由于压力的单位是kPa,因此功的单位是kJ。 例3.2直径为110mm的气缸中有60℃的水100cm,一个50kg的活塞放在水面上。加热至 温度达到200℃,求所作的功。 解国”气缸中的压力是由于活塞的重量引起的并保持恒定。假定是无摩擦密封(我们总是这样 假设除非有相反的信息给出)。力的平衡为 mg=PA-P.-A,(50)(9.81)=(P-10000)0.110, P=151600Pa 4 因为上式使用了大气压力所以结果是绝对压力。初始状态①的容积为 V,=100×10s=104m3 利用60℃的功,质量可计算得 m-告-a8o7=a98a3ke 104

第三章功和热量 ·29· 状态②的温度为200℃,压力是0.15MPa(该压力与0.1516MPa相差在1%以内,是可以接受的)。 容积为 V3=m2=(0.09833)(1.444)-0.1420m3 最后,可计算功为 W=P(V2-V)-=151(600)(0.1420-0.0001)=21500(J)或21.5(kJ) 例3.3能量被加入到一个活塞一气缸装置中。活塞被压回以保持PV恒定。初始压力和容 积分别为200kPa和2m3。如果最终的压力是100kPa,计算气体对活塞所作的功。 解辄中式(3.4)得功为 w..-pw-Gov 这里我们利用了PV=C这一关系。为了计算功必须求得C和V:。常数C可由下式求得 C=P,V1=(200)(2)=400(kJ) 为求得V2,我们用P,V,=PV,这一关系式自然是涉及理想气体等温过程(温度恒定)的方程。该 式可以写成 V,-P'=20②2=4m) P2 100 最后, w:-4w=40oh音=277) 该值为正,因为膨胀过程中系统(气缸中的气体)对外作功。 例3.4请确定一个以90k/h的速度行驶的流线型汽车,克服风的阻力所需要的马力。风 的阻力系数C为0,2,阻力用Fo-pWAC,计算,其中A是汽车的投影面积,V 是速度。空气密度p为1.23kg/m。取A=2.3m3。 解球为了求解作用于汽车上的阻力,我们必须将速度转化为以m/s为单位:V=(90)(1000/ 3600)=25m/5。于是阻力为 F=2wAC0=(号)1.23(25)2.30.21=177(N0 为了克服在25m/3速度下的这-阻力,发动机必须作的功率为 W=FnV-(177)(25)=4425(W) 则相当于 4425W=5.93hp 746 W/hp 3.4非平衡功 必须强调的是,PV图上的面积仅代表准平衡过程的功。非平衡过程的功不能用PdV 计算;它要么对于特殊过程是已知的,要么必须用其他方法确定。现在给出两个例子。考虑图 3-5中由气体形成的系统。在(a)中功明显地通过旋转的轴穿越了系统边界;但容积没有改 变。忽略滑轮系统的摩擦,我们可以通过重量和下落距离的乘积来计算输人的功。然面,它不 气体 真空 气体 {b) 图3-5
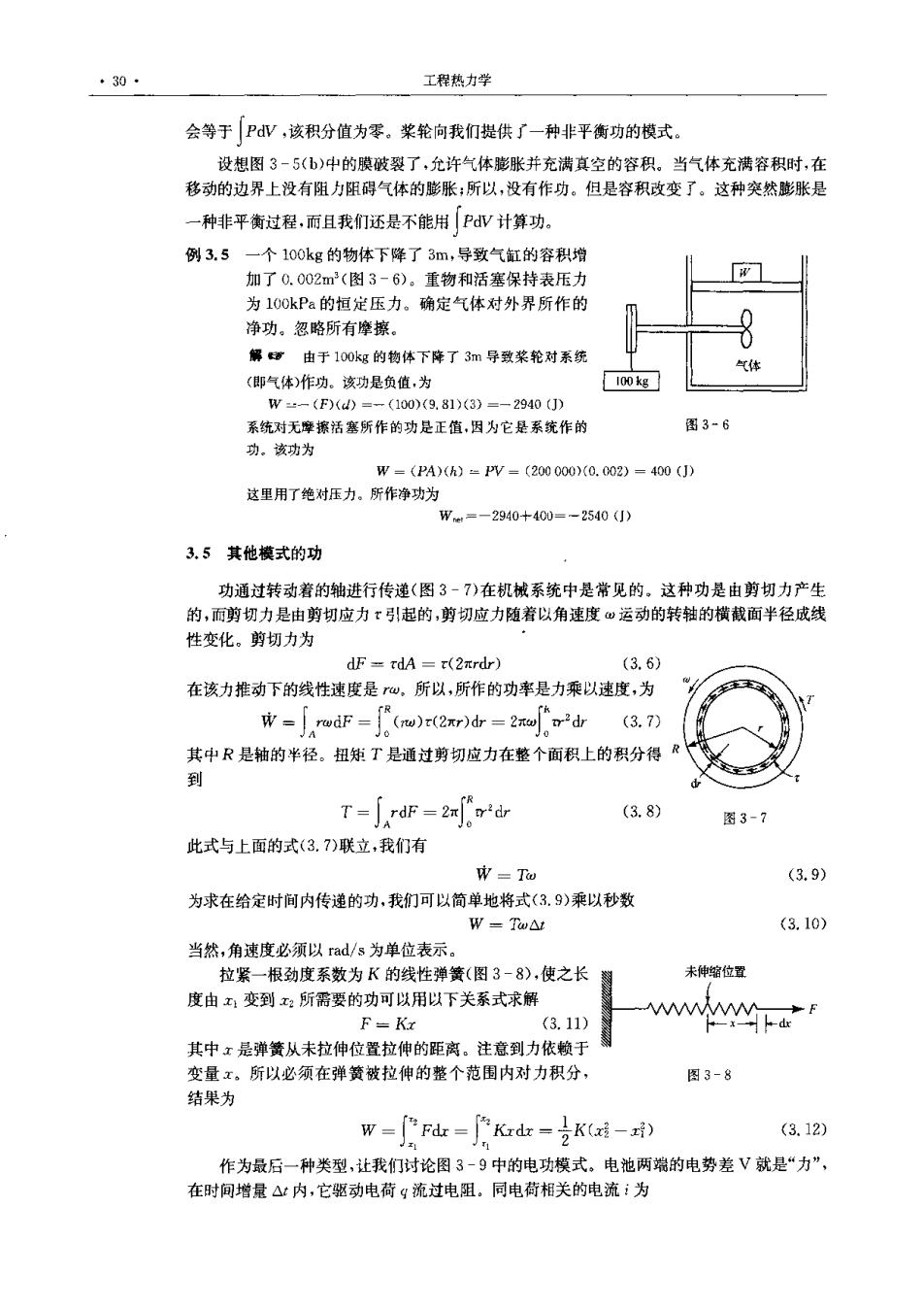
*30· 工程热力学 会等于PW,该积分值为零。桨轮向我们提供了一种非平衡功的模式。 设想图3-5(b)中的膜破裂了,允许气体膨胀并充满真空的容积。当气体充满容积时,在 移动的边界上没有阻力阻碍气体的膨胀;所以,设有作功。但是容积改变了。这种突然膨胀是 一种非平衡过程,而且我们还是不能用|PW计算功。 例3.5一个100kg的物体下降了3m,导致气缸的容积增 加了0.002m3(图3-6)。重物和活塞保持表压力 为100kPa的恒定压力。确定气体对外界所作的 净功。忽略所有摩擦。 解道由于100kg的物体下降了3m导致桨轮对系统 气体 (即气体)作功。该功是负值,为 W--(F)(d)=一(100)(9.81)(3)=一2940(J) 系统对无摩擦活塞所作的功是正值,因为它是系统作的 图3-6 功。该功为 W=(PA)(h)=PV=(200000)(0.G02)=400(J) 这里用了绝对压力。所作净功为 We=一2940+400=-2540(J) 3.5其他模式的功 功通过转动着的轴进行传递(图3-7)在机械系统中是常见的。这种功是由剪切力产生 的,而剪切力是由剪切应力τ!起的,剪切应力随着以角速度w运动的转轴的横截面半径成线 性变化。剪切力为 dF=xdA=t(2πrdr) (3.6) 在该力推动下的线性速度是心。所以,所作的功率是力乘以速度,为 wF(u)(dr-2mdr (3.7) 其中R是轴的半径。扭矩T是通过剪切应力在整个面积上的积分得R 到 (3.8) 图3-7 此式与上面的式(3.7)联立,我们有 W-Tw (3.9) 为求在给定时间内传递的功,我们可以简单地将式(3.9)乘以秒数 W=Tw△t (3.10) 当然,角速度必须以rad/s为单位表示。 拉紧一根劲度系数为K的线性弹簧(图3-8),使之长 未伸缩位置 度由x:变到x2所需要的功可以用以下关系式求解 WWWWM F=Kx (3.11) de 其中x是弹簧从未拉伸位置拉伸的距离。注意到力依赖于 变量x。所以必须在弹簧被拉伸的整个范围内对力积分, 图3-8 结果为 w=Fu=kdr=号Kxi-) (3.12) 作为最后一种类型,让我们讨论图3-9中的电功模式。电池两端的电势差V就是“力”, 在时间增量△t内,它驱动电荷g流过电阻。同电荷相关的电流i为

第三章功和热量 ·31· idg (3.13) 电流 d 对于恒定电流,电荷为 电池 R电阻 9=i△t (3.14) 则这个模式的非平衡功为 W=Vi△r (3.15) 图3-9 功率就是作功的速率,或 w=Vi (3.16) 这个关系实际上被用来定义电势,电压V,因为安培是基本单位,而瓦特已经被定义过了。 一伏特等于一瓦特除以一安培。 例3.6汽车的驱动轴在转数3000r/min时扭矩为100N·m。计算被释放的马力数。 解功率由W=-Ta计算,这要求u以rad/s为单位: u=(300)2x)(高)-314.2ad/s 所以W=(10)3.2)=31420(w0或到祭=21p) 例3.7加热圆形气缸(图3-10)中的空气直到弹簧被压缩了 猴 50mm。求空气对无摩擦活塞所作的功。弹簧开始没有伸 缩。 K=2500 N/m 解切由力平衡可得气缸中的初始压力: PA]=PA+W, 50 kg P0,1)=1000000,12'+(50(9.81) 4 4 P=1625C0Pa 在没有弹簧的情况下活塞升高50mm,则压力是恒定的,功是力与距 -20cm 离的乘积 W=PA×d(16250)x01D(0.05)=63.81) 图3-10 利用式(3.12)压缩弹簧所需要的功可计算为 W受K(-对)=(号)(250)(0.5)-3.1250) 总的功是上面两个值的和:Wm=63.81+3.125=66.94(J)。 3.6热量 在前述各节中我们考查了几种功的模式,通过这些模式,能量宏观地传入系统或者从系统 传出。能量还可以通过分子间的相互作用微观地传入系统或者从系统传出。这些分子来自系 统表面或者外界表面。如果系统边界的分子比外界边界的分子更活跃,则通过快的分子将能 量传递给慢的分子,这些分子将把能量从系统传到外界。在这一微观尺度上,能量的传递是通 过功的形式:粒子间的碰撞来实现的。力发生在极为短的时间段中,功将能量从快的分子传递 给慢的分子。我们的问题在于,这些微观的能量传递方式,在宏观上无法以任何功的模式观察 到:我们必须设计一个宏观的量以计算这些微观的能量传递。 我们已经注意到温度这个性质随分子活动的增加而增加。所以我们将微观的能量传递与 宏观性质温度联系起来是不奇怪的。这种我们无法用任何一种宏观功的模式计算的宏观能量 传递叫做热量。热量是由系统及其外界间存在的温度差引起的穿越系统边界的能量传递。系 统并非具有热量,而是具有能量,热量是传递中的能量。 为了举例说明,考虑质量相等的一热一冷两块物体,热的那块比冷的那块具有更多的能 量,因为它的分子更活跃,具有更高的温度。当将这两块互相接触时,能量依靠传热从热的那