
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY Engineering Thermodynamics I Lecture 47 Chapter 9 Gas Power Systems (section 9.10) Spring,5/9/2019 强 Prof.,Dr.Yonghua HUANG VMLLMMAAD 目e http://cc.sjtu.edu.cn/G2S/site/thermo.html 1日G
Engineering Thermodynamics I Lecture 47 Spring, 5/9/2019 Prof., Dr. Yonghua HUANG Chapter 9 Gas Power Systems (section 9.10) http://cc.sjtu.edu.cn/G2S/site/thermo.html
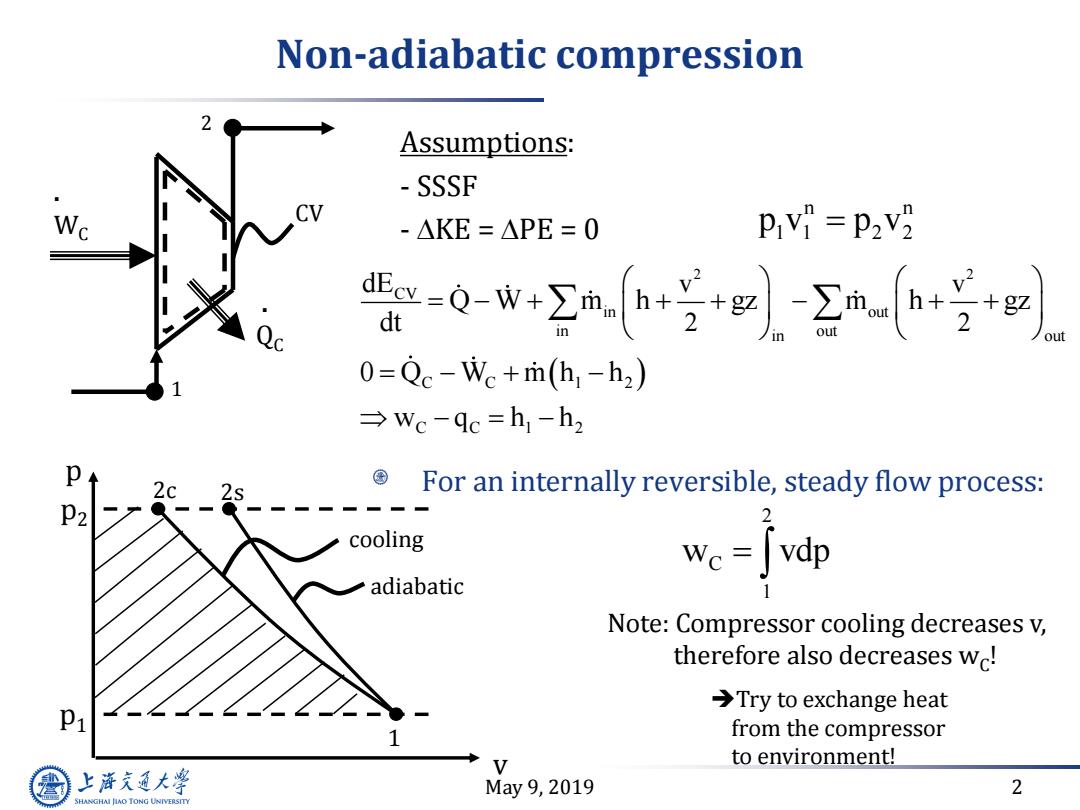
Non-adiabatic compression Assumptions: SSSF W -△KE=△PE=0 -0+2a宁l-2++ out 0=Qc-Wc+m(h-h2) →wc-qc=h1-h2 国 For an internally reversible,steady flow process: P2 2 cooling we Jvdp adiabatic 1 Note:Compressor cooling decreases v, therefore also decreases wc! >Try to exchange heat P1 from the compressor to environment! 上游充通大 May9,2019 2 SHANGHAI JIAO TONG UNIVERSITY
May 9, 2019 2 Non-adiabatic compression 2 2 CV in out in out in out C C 1 2 C C 1 2 v v 2 2 dE Q W m h gz m h gz dt 0 Q W m h h w q h h Assumptions: - SSSF - KE = PE = 0 1 2 . WC . QC CV v 1 2s p p2 p1 2c cooling adiabatic For an internally reversible, steady flow process: 2 C 1 w vdp Note: Compressor cooling decreases v, therefore also decreases wC ! Try to exchange heat from the compressor to environment! n n 1 1 2 2 p v p v
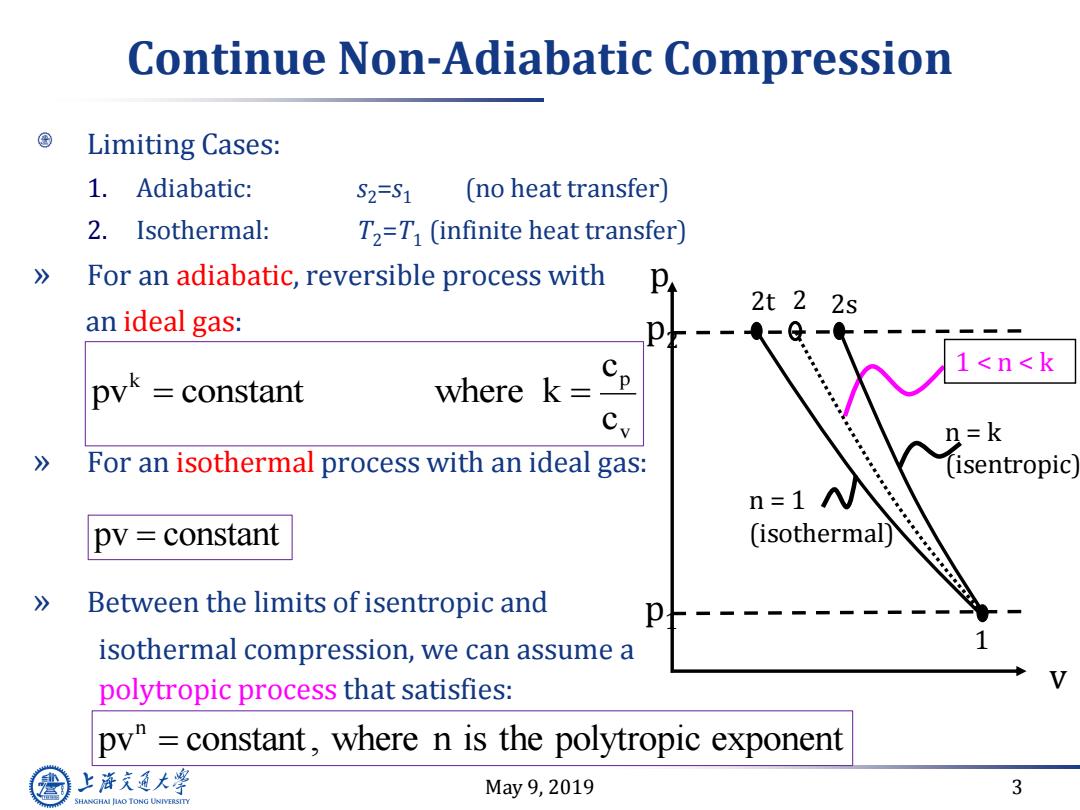
Continue Non-Adiabatic Compression Limiting Cases: 1.Adiabatic: S2=S1 (no heat transfer) 2.Isothermal: T2=T (infinite heat transfer) 》 For an adiabatic,reversible process with 2t22s an ideal gas: a-@ 1<n<k pyk =constant where k= 2=k 》 For an isothermal process with an ideal gas: (isentropic n=1 N pv constant (isothermal) 》 Between the limits of isentropic and isothermal compression,we can assume a polytropic process that satisfies: py"constant,where n is the polytropic exponent 上游究通大粤 May9,2019 3 SHANGHAI JLAO TONG UNIVERSITY
May 9, 2019 3 Continue Non-Adiabatic Compression Limiting Cases: 1. Adiabatic: s2=s1 (no heat transfer) 2. Isothermal: T2=T1 (infinite heat transfer) » For an adiabatic, reversible process with an ideal gas: » For an isothermal process with an ideal gas: » Between the limits of isentropic and isothermal compression, we can assume a polytropic process that satisfies: k p v c pv constant where k c pv constant n pv constant , where n is the polytropic exponen t v 1 2s p p2 p1 1 < n < k 2t 2 n = k (isentropic) n = 1 (isothermal)

Continue Non-Adiabatic Compression For any internally reversible process:W-dp For a polytropic process n1 w--ntpv.-pv] n≠1 we--n-R(G-T) n For an ideal gas n≠1 For an isothermal process n =1 We =-P:V In(p2 /p)=-P:V In(Vi V2) n=1 For an ideal gas We=-RTIn(P2/P) n=1 上游充通大学 May9,2019 4 SHANGHAI JLAO TONG UNIVERSITY
May 9, 2019 4 Continue Non-Adiabatic Compression For any internally reversible process: For a polytropic process For an isothermal process 𝑊c = − න 1 2 𝑣𝑑𝑝 C 2 2 1 1 n w p v p v n 1 n 1 For an ideal gas C 2 1 n w R T T n 1 n 1 n 1 w p v ln(p / p ) p v ln(v / v ) n 1 C 1 1 2 1 1 1 1 2 For an ideal gas w RTln p / p n 1 C 2 1 n 1

Two-stage Compression with Intercooling 2 Intercooler T P2 P2 2s 2s Px 2 P1 2 T 1 Ti 2t S S 图 上游充通大学 May9,2019 5 SHANGHAI JIAO TONG UNIVERSITY
May 9, 2019 5 Two-stage Compression with Intercooling s T 1 x t=y 2 2s x x s 2t T1 p2 px p1 qI air x Intercooler wc 2 y 1 1 1 2 . WC . QC CV s T 1 2 2s T1 p2 p1