
·2· 工程热力学 然后用控制容积进行研究。 1.3宏观描述 在工程热力学中我们假定系统或控制容积中的物质是连续介质,即:它们在我们所关注的 区域内连续分布。这一假定使我们仅用少数儿个可测量的性质就能描述一个系统或控制容 积。 密度的定义为: p=器 (1.1) 其中△m是△V的容积内所含的质量,如图】-3所示。物理上,△V不允许缩小到零,因为如 果△V变得极小,△m的变化将依靠△V中的分子数目而不再连续。所以P定义中的零应该由 某个小的量e代替,其大小又足够消除分子的影响。注意到在标准条件下1m3的空气里含 有约3×10个分子,因而e不棉要太大就可以含有以十亿计的分子。对大多数工程应用来 说,e非常的小,以至于我们可以认为其像式(1.1)中那样趋近于零。 较稀的 容积4/ 物质 较浓的 图1-3 不过,在有些情况下连续介质假设并不正确。比如:人造卫星重返大气层。在海拔 100km处,一个分子在碰撞到其他分子前所运动的平均距离,即分子的平均自由程,是大约 30mm,宏观的研究方法已经靠不住。在海拔150km处平均自由程超过3m,这一尺度已经和 人造卫星的大小相当!在这种情况下,必须采用建立在分子行为基础上的统计方法。 1.4系统的状态与性质 系统中的物质可以以数个相存在:固相、液相或气相。相中的物质具有均匀一致的化学组 成。相边界将不同的相分隔开,如果将这些不同的相作为一个整体,则称之为混合物。 性质是用来描述系统的量。系统的状态是在某一舜间系统的情况,它是用性质的给定值 来描述的。常见的性质有压力、温度,容积、速度以及位置,不过有时候也需要考虑其他性质。 当表面效应很显著时,形状是一个很重要的性质:当考查辐射换热时,顏色也很重要。 性质的基本特征是当系统处于某一状态时,性质具有惟一的值,而且该值不取决于系统以 前所经历的状态,简而言之,性质不是过程的函数。因为性质不取决于过程,所以其任何变化 仅取决于系统的初始和终了状态,用符号中表示一个性质,则有如下数学表达式: 作d9=-4 (1.2) 这要求d协是一个精确微分:中一,代表当系统从状态1变化到状态2时性质的变化。我们还 将遇到像功这样的量,它们是过程的函数,对这些量来说,严格的微分是不存在的。 相对较少的独立性质就能确定系统所有的其他性质和系统的状态,如果系统是单相的,而 且不受磁场、电场和表面效应的影响,那么任何两个性质就可以确定系统的状态。在工程热力 学中,这种简单系统颇受关注。 热力学性质分为两大类:强度性质和广延性质。强度性质与系统的质量无关,温度、压力

第…章概念,定义和基本原理 ·3· 密度和速度就是强度性质,因为它们对于整个系统或系统的一部分来说是一致的。如果我们 将两个系统合二为一,强度性质是不能求和的。 广延性质是与系统的质量相关的性质。容积、动量以及动能就是广延性质。如果将两个 系统合二为一,则新系统的广延性质是原先两个系统广延性质的和。 如果我们将广延性质除以质量就会得到比性质。比体积就是这样定义的: 。岩 (1.3) 我们通常会用一个大写字母表示一个广延性质[例外:质量用m表示]并用一个小写字母表示 相关的强度性质。 1.5热力学平衡:过程 当淡到一个系统的温度或压力时,我们假定该系统内部所有点都具有相同的或基本相同 的温度或压力。若这些性质在系统中的点与点之间是恒定的,而且这些性质没有随时间变化 的趋势,则这样的状态就是热力学平衡状态。如果系统边界上某部分的温度,比方说突然增 加,则温度将自发地重新分布,直到系统的所有部分处于同一温度之下。 一个系统如果受到某个小的扰动其性质将有大的变化,则称该系统处于准稳态平衡。汽 油和空气的混合物,或放在一张极小桌子上的一个大碗就是这样的系统。 当系统从一个平衡态变化到另一个平衡态时,系统所经历的一系列连续的状态称之为过 程。如果在从一个状态变化到另一个状态时,与平衡态的偏差无限小,则该过程为准平衡过 程,该过程的每一个状态都可以被理想化为一个平衡态。很多过程,像内燃机中气体的压缩和 膨胀,都可以近似为准平衡过程,近似并不引起准确度的显著下降。如果一个系统经历了一个 准平衡过程(如空气在气缸中被缓慢地压缩),则该过程可以用一条实线画在一个合适的坐标 系中,如图1-4()所示。如果一个系统从一个平衡态到另一个平衡态中间经历了一系列非 平衡态(如燃烧),我们说系统经历了一个非平衡过程。在图1-4(b)中以虚线画出的曲线表 示这样一个过程:在(V1,P)和(V2,P2)两状态之间,整个系统各处的性质并不相等,因而系统 的状态不能很好地确定。 P P 而 (b) 图1-4 例1,1对子一个特定的过程来说,它是一个准平衡过程还是一个不平衡过程,取决于这一过 程是如何实现的。让我们将重物W加到图1-5中的活塞上。如果该重物是突然地 一次全部加到活塞上,如(a》所示,则会引发气体系统的不平衡过程。如果我们将该 重物分成许多份,每次只加上其中的一份,如(b)所示,则气体将经历一个准平衡过 程。 注意在平衡的概念中外界并不起作用,这是合理的,因为外界是通过摩擦对系统做功:对 于准平衡过程来说,只要求在过程的任一瞬时,系统的性质是均的
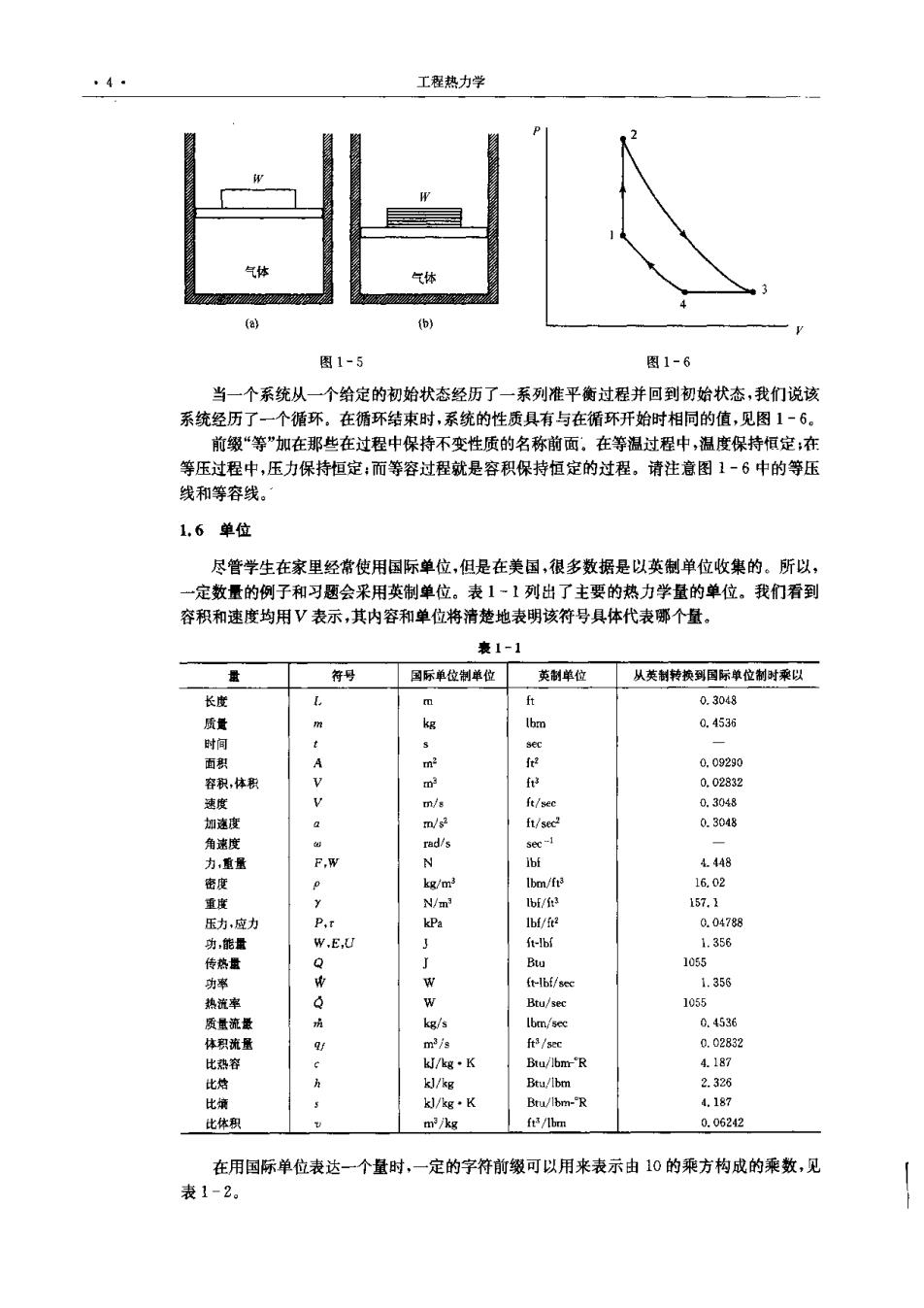
4▣ 工程热力学 体 (b) 图1-5 图1-6 当一个系统从一个给定的初始状态经历了一系列准平衡过程并回到初始状态,我们说该 系统经历了一个循环。在循环结束时,系统的性质具有与在循环开始时相同的值,见图1~6。 前缀“等”加在那些在过程中保持不变性质的名称前面。在等温过程中,温度保持恒定;在 等压过程中,压力保持恒定:而等容过程就是容积保持恒定的过程。请注意图1~6中的等压 线和等容线。 1.6单位 尽管学生在家里经常使用国际单位,但是在美国,很多数据是以英制单位收集的。所以, 一定数量的例子和习题会采用英制单位。表1~1列出了主要的热力学量的单位。我们看到 容积和速度均用V表示,其内容和单位将清楚地表明该符号具体代表哪个量。 表1-1 量 符号 国际单位制单位 英制单位 从英制转换到国际单位制时乘以 长度 L 0.3048 质: m kg Ibm 0.4536 时间 sec 面积 m2 f2 0.09290 容积,体积 m? fe 0.02832 速度 m/s ft/sec 0.3048 加速度 e m/s2 ft/sec2 0.3048 角速度 u rad/s sec-1 力,直量 F.W N Ibf 4.448 密度 kg/m3 Ibm/ft3 16.02 重度 N/m3 Ibf/f 157.2 压力,应力 P,t kPa Ibf/ft2 0.04788 功,能量 W.E,U J ft-lbf 1.356 传热量 Q J Btu 1055 功率 (t-Ibf/sec 1.356 热流率 Q W Btu/sec 1055 质量流撒 疗 kg/s Ibm/sec 0.4536 体积流量 q时 ma/s ft3/sec 0.02832 比热容 k/kg·K Btu/lbmR 4.187 比焙 kl/kg Btu/lbm 2.326 比境 k/kg·K Btu/lbm-R 4.187 比体积 mi/kg ft/Ibm 0.06242 在用国际单位表达一个量时,一定的字符前缀可以用来表示由10的乘方构成的乘数,见 表1-2

第一章概念、定义和基本原理 ·5· 表1-2 乘数 前缀 符号 乘数 前级 符号 1012 tera T 10-3 milli m 109 giga G 10-5 micro 和 106 mega M 10-9 nano n 103 kilo k 10一12 pico 10-2 centi c 除用于cm,n2或am3外一般不用 不同量的单位通过这些量所遵循的物理定律相互关联。于是,在任何一个单位体系中,所 有的单位均可表示成一系列基本单位的代数组合。在国际单位制中有七个基本单位:,kg, s,K,mol(摩尔),A(安培),cd(堪德拉)。其中后两个在工程热力学中极少碰到。 例1.2牛顿第二定律F=m,将作用在物体上的净力与物体的质量与加速度联系了起来。 于是,一牛顿的力使一千克质量的物体具有一m/s2的加速度,或是一lhf的力使 32.21bm(1slug)的物体具有一ft/sec2的加速度。因此,这些单位有如下关系: 1N=1kg·m/s2或11bf=32.2lbm-ft/sec2 例1.3重力是地心引力的结果。根据牛顿第二定律,W=mg,当质量保持恒定,W随海拔高 度发生改变是由于重力加速度g的变化(从最高的山上的9.77/s2到最深的海沟处 的9.83m/s2)。除非另有说明,我们将使用9.81m/s(32.2ft/sec2)作为重力加速度 的标准值。 例1.4为了用国际单位制的基本单位表达能量的单位J(焦耳),我们用能量或功是力与距离 的乘积这一概念,并根据例1.2, 1J=(1N)(1m)=(1kg·m/s2)(1m)=1kg·m2/s2 在英制单位中,lbf和bm都是基本单位,如表1~1所示,能量的主单位是ft-bf。由 例1.2得 1 ft-lbf=32.2 Ibm-ft2/sec2=1 slug-ft2/sec2 这与在国际单位制中的关系是类似的。 1.7密度、比体积、量度 根据式(1.1),密度是单位容积的质量:根据式(1.3),比体积是单位质量的容积。因此, = (1.4) 与(质量)密度相关的是重量密度或称之为重度Y: 7-W (1.5) 其单位为N/m(Ibf/ft)。[注意,Y是容积的比性质而不是质量的比性质.]通过W=mg,重 度与密度被关联了起来: Y=Ag (1.6) 对于水来说,p和Y的标准值分别是1000kg/m3(62.4bm/ft3)和9810N/m3(62.4lbf/fr)。 对于空气来说,其标准值分别是1.21kg/m(0.07551bm/ft)和11.86N/m3(0.07551bf/ ft3)。 例1.5已知-一个3×5×20m的房间中的空气质量为350kg,求其密度、比体积和重度。 p-号=3》2o=1.167em,=日-i-0.sm/g Y=g=(1.167)(9.81)=11.45N/m2

·6· 工程热力学 1.8压力 定义 对气体和液体来说,在一面积上的垂直作用力称为压力。如果一个力△F是以一定角度 作用在一面积△A上(图1-7)。则只有该力的垂直分量△F,可以计人压力的定义当中: P=祭 (1.7) 在国际单位制中,压力的单位是帕斯卡(Pa) 表面 1Pa=1N/m2=1kg/m·s2 相应的英制单位是1bf/ft,通常还用bf/in2(psi)作 压力的单位。 通过考查压力对固定深度下三角形流体单元的 作用,我们可以看到,在处于平衡状态(不运动)的流 图1-7 体中,其中一点的各个方向的压力均相同:压力是一 个标量。对于气体和液体来说,在相对运动的状态 下,流体中一点的压力会随方向变化:不过,这种变化极其徽小,对于大多数低黏度气体和液体 (如:水)来说可以忽略。在以上的讨论中,我们没有假设压力从一点到另一点是不变化的,只 有在单独的点上压力不随方向变化。 压力随海拔高度的变化 在大气层中,压力是随海拔高度变化的。这一变化可以通过考查图1-8所示的空气单元 的平衡,用数学方法表达。在垂直方向(向上为正)作用在单元上的合力为 dP=一gdz (1.8) 如果P是之的已知函数,则可以对上式积分以 压力的作用力:(P+dPM 得到P(x): P(z)-Po=-cdz (1.9) 面积A 对液体,p是常数。若令dh=一dz,则可 重力:p84也 将式(1.8)写成 dP=ydh (1.10) 其中h是被测位置的高度,方向向下。以P= 压力的作用力:PA 0的液体表面为积分起点,积分该式可得 P=7h (1.11) 这一方程可以将以米水柱和毫米汞柱为单位 Po 的压力转化为以Pa为单位。 在多数热力学关系式中必须用绝对压力。 图1-8 绝对压力是表压力与大气压力之和。 Pba=Pge十Pm (1.12) 负的表压力通常被称为真空,能够读取负压的表叫做真空表。一50kPa的表压力被称为 50kPa的真空,前面的负号被省略。 图1~9表示了绝对压力和表压力间的相互关系。 “表压”这个词通常会用在对表压力的表述中。如:P=200kPa表压。如果没有“表压”一 词,通常是指绝对压力。大气压力是一个绝对压力,如果没有另外的说明,其值可认为等于 100kPa(在海平面上)。应该注意的是,大气压力在很大程度上取决于海拔高度:在科罗拉多 州的丹佛,大气压力为84kPa,而在一个海拔3000m的山城,大气压力只有70kPa