
第二节 确定型存储模型 所以单位时间的订货费为: C3 C3R R 在不允许缺货的情况下,最高存货量为Q, 最低存货量为0,单位时间平均存货量是Q/2,所 以单位时间的存储费为CQ/2,单位时间的存储 总费用为: C3R C(Q)= C 2 18
18 所以单位时间的订货费为: Q C R R Q C t C 3 3 3 在不允许缺货的情况下,最高存货量为Q, 最低存货量为0,单位时间平均存货量是Q/2,所 以单位时间的存储费为C1Q/2 ,单位时间的存储 总费用为: 1 3 2 ( ) C Q Q C R C Q 第二节 确定型存储模型
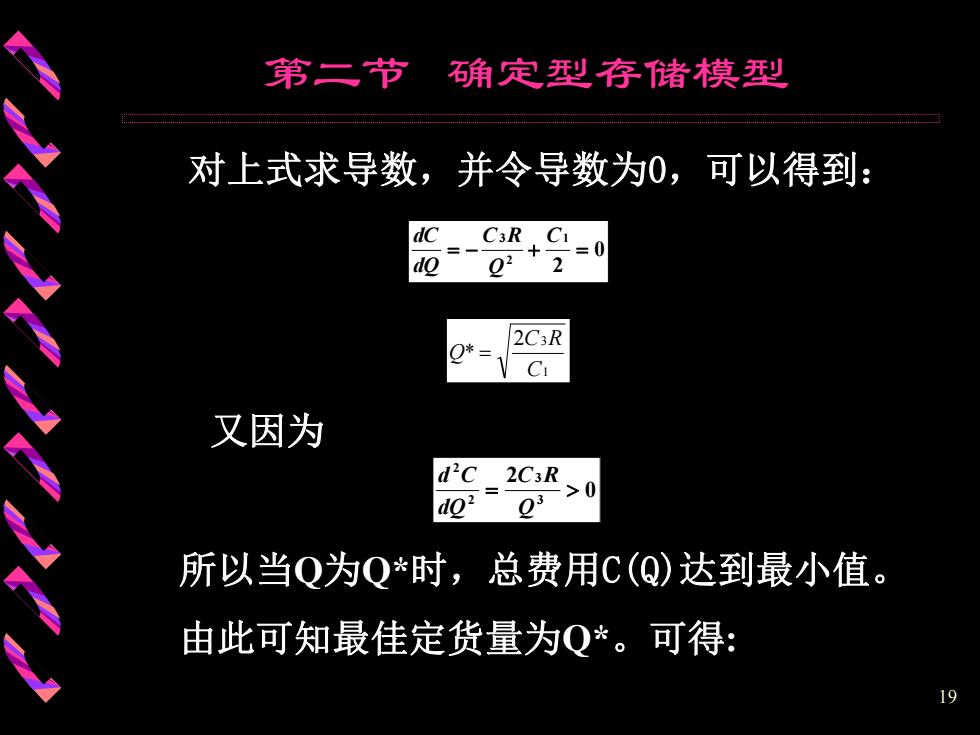
第二节 确定型存储模型 对上式求导数,并令导数为0,可以得到: dC C3R C1 =0 do 2 2C3R CI 又因为 dc 2C3R >0 do? 23 所以当Q为Q*时,总费用C(Q)达到最小值。 由此可知最佳定货量为Q*。可得: 19
19 对上式求导数,并令导数为0,可以得到: 0 2 1 2 3 C Q C R dQ dC 又因为 所以当Q为Q*时,总费用C(Q)达到最小值。 由此可知最佳定货量为Q* 。可得: 1 2 3 * C C R Q 0 2 3 3 2 2 Q C R dQ d C 第二节 确定型存储模型

第二节 确定型存储模型 2C3 R RC1 即每隔时间t*订货Q*是该系统的最佳存储策 略。 例1某种商品每天的需求量为100单位,每 次发出订单的订货费为100元,每单位货物每天 的存储费为0.02元。如果不允许缺货,且发出订 单即能收到货物,问经济批量是多少?如果拖后 时间为3天,最佳策略是什么? 20
20 即每隔时间t *订货Q *是该系统的最佳存储策 略。 例1 某种商品每天的需求量为100单位,每 次发出订单的订货费为100元,每单位货物每天 的存储费为0.02元。如果不允许缺货,且发出订 单即能收到货物,问经济批量是多少? 如果拖后 时间为3天,最佳策略是什么? 1 3 * * 2 RC C R Q t 第二节 确定型存储模型

第二节 确定型存储模型 解: 由题意可知C3=100元/次,R=100单 位/天,C1=0.02元/天、单位。 因此,经济批量为1000单位, 每隔10天发一 张订单。 如果拖后时间为3天,经济批量和订货间隔 不变,只要在用完存货的前3天,即存货量为300 单位时发出订货单,使得存货用完时订货刚好到 达 21
21 解: 由题意可知C3 =100元/次,R=100单 位/天,C1 =0.02元/天、单位。 因此,经济批量为1000单位,每隔10天发一 张订单。 如果拖后时间为3天,经济批量和订货间隔 不变,只要在用完存货的前3天,即存货量为300 单位时发出订货单,使得存货用完时订货刚好到 达。 第二节 确定型存储模型

第二节 确定型存储模型 在上述探讨经济批量的过程中,我们没有考 虑到货物的成本费,这是因为与成本费相关的货 物单价K与经济批量是无关的。在单位时间的需 求量为常数R的情况下,单位时间内的成本费是 常数KR,它不随Q和t的大小而变化,所以不影响 Q和t的选择。如果将该项费用加入到单位时间的 存储总费用C(Q)中去,由于它是常量,导数是零 不会出现在Q*的表达式中。所以此时考虑最优 存储策略可以不考虑成本费这个因素 22
22 在上述探讨经济批量的过程中,我们没有考 虑到货物的成本费,这是因为与成本费相关的货 物单价K与经济批量是无关的。在单位时间的需 求量为常数R的情况下,单位时间内的成本费是 常数KR,它不随Q和t的大小而变化,所以不影响 Q和t的选择。如果将该项费用加入到单位时间的 存储总费用C(Q)中去,由于它是常量,导数是零, 不会出现在Q*的表达式中。所以此时考虑最优 存储策略可以不考虑成本费这个因素。 第二节 确定型存储模型