PEA Problem Setup Question 1 Question 2 Question 3 00行00 ==mm==■m 。----=。== Advice,1 Advice,2 Advice,3 1 1 Advice2 1 Advice22 Advice2 3 Experts Advice,1 Advice32 Advices3 Advice,1 Advice,2 Advice3 Learner Answer 1 Answer 2 Answer 3 Advanced Optimization(Fall 2023) Lecture 6.Prediction with Expert Advice 6
Advanced Optimization (Fall 2023) Lecture 6. Prediction with Expert Advice 6 PEA Problem Setup Question 1 Question 2 Question 3 Advice1 1 Advice1 2 Advice1 3 Advice2 1 Advice2 2 Advice2 3 Advice3 1 Advice3 2 Advice3 3 Advice4 1 Advice4 2 Advice4 3 Experts Learner Answer 1 Answer 2 Answer 3

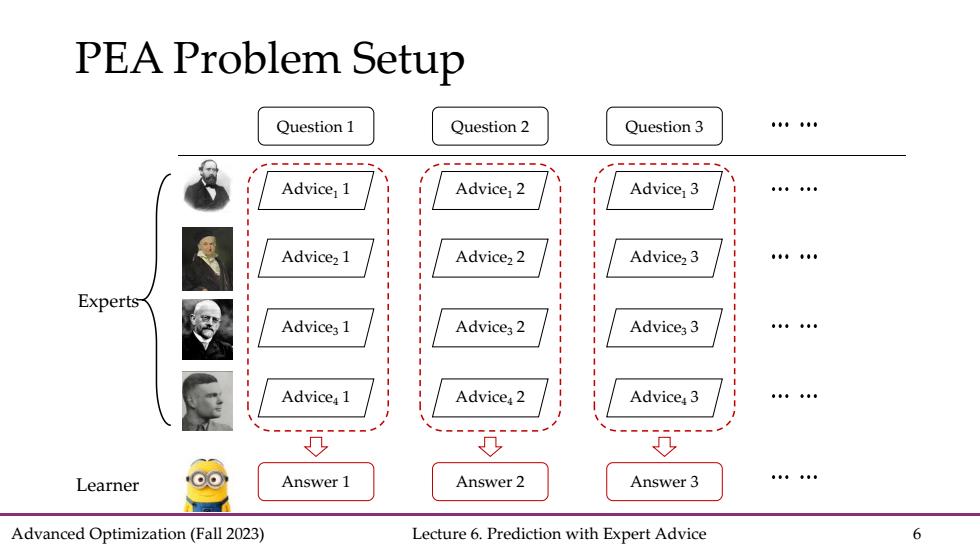
PEA:Formulization The online learner(player)aims to make the prediction based by combining N experts'advice. At each round t=1,2,... (1)the player first picks a weight p from a simplex AN; (2)and simultaneously environments pick a loss vector eERN; (3)the player suffers loss fi(p:)(p,e),observes e and updates the model. The feasible domain is the(W-l)-dim simplex△v={p∈Rv|p,≥0,∑1pi=l} We typically assume that0≤lt,i≤1holds for all t∈[T]andi∈[W]. Advanced Optimization(Fall 2023) Lecture 6.Prediction with Expert Advice 7
Advanced Optimization (Fall 2023) Lecture 6. Prediction with Expert Advice 7 PEA: Formulization • The online learner (player) aims to make the prediction based by combining N experts’ advice

PEA:Formulization The online learner(player)aims to make the prediction based by combining N experts'advice. At each round t=1,2,... (1)the player first picks a weight p from a simplex AN; (2)and simultaneously environments pick a loss vector eERN; (3)the player suffers loss fi(p)(p,e),observes e:and updates the model. The goal is to minimize the regret with respect to the best expert: T T t iE(N] Advanced Optimization(Fall 2023) Lecture 6.Prediction with Expert Advice 8
Advanced Optimization (Fall 2023) Lecture 6. Prediction with Expert Advice 8 PEA: Formulization • The online learner (player) aims to make the prediction based by combining N experts’ advice. • The goal is to minimize the regret with respect to the best expert:

A Natural Solution Follow the Leader (FTL) Select the expert that performs best so far,specifically, pL=arg min (p,Ln-)=argmin L-1, pE△N ie[N] where L-l∈Nis the cumulative loss vector withL-l,i≌∑ls,i T 61,1=0.49 → 21=1 83,1=0 Regr=∑p,L,)-a∑i t=1 N]1 T 2 =O(T) 61,2=0.51 2,2=0 3,2=1 FTL achieves linear regret in the worst case! Advanced Optimization(Fall 2023) Lecture 6.Prediction with Expert Advice 9
Advanced Optimization (Fall 2023) Lecture 6. Prediction with Expert Advice 9 A Natural Solution • Follow the Leader (FTL) Select the expert that performs best so far, specifically, FTL achieves linear regret in the worst case!

A Natural Solution Follow the Leader (FTL) Select the expert that performs best so far,specifically, p=arg min (p,L-1)=argmin L-1 pE△N iE[N] whereRN is the cumulative loss vector with. Pitfall:decision is actually a one-hot vector,which can be very unstable. Replacing the 'max'operation in FTL by 'softmax'. Advanced Optimization(Fall 2023) Lecture 6.Prediction with Expert Advice 10
Advanced Optimization (Fall 2023) Lecture 6. Prediction with Expert Advice 10 A Natural Solution • Follow the Leader (FTL) Select the expert that performs best so far, specifically, Pitfall: decision is actually a one-hot vector, which can be very unstable. Replacing the ‘max’ operation in FTL by ‘softmax’