西北农林科技大学：《田间试验与统计分析》课程教学课件（PPT讲稿）第2章 统计假设测验及T检测 2.4 二项资料的百分数假设检验 Test of percent hypothesis 2.5 参数的区间估计 Estimate of confidence interva

两个样本百分数相比较的假设测验 ·例题：调查一低洼地，小麦378株，其中有锈病355株， 病株率93.92%，一高地调查396株，有346株发病，病株 率为87.37%。问两块田发病情况有无差异？ ·n1=378,X1=355,n2=396,X2=346 p1=93.92 p2=87.37 假设：H0:p1=p2:Hap1≠p2:a=0.05, 作两尾测验uo5=1.96

• 例题：调查一低洼地，小麦378株，其中有锈病355株， 病株率93.92％，一高地调查396株，有346株发病，病株 率为87.37％。问两块田发病情况有无差异？ • n1=378，x1=355，n2=396，x2=346 p ˆ 1 = 93.92 p ˆ 2 = 87.37 假设： H0：p1=p2； HA：p1 ≠ p2；α=0.05， 作两尾测验u.05=1.96。 两个样本百分数相比较的假设测验

两个样本百分数相比较的假设测验 计算：刀=+=35+346-0906g=1-0906=0094 n1+n2378+396 +1 =0.021 378396 4=B-22-0.09392-0.8737 =3.12 0p- 0.021 因为：u05=1.96,|u川3.12>0.05，所以p<0.05。 推断：否定Ho:p1=p2,接受HA:pp2,即该试验中两块麦 田锈病的发生程度有显著差异

0.906, 1 0.906 0.094 378 396 355 346 1 2 1 2 = = − = + + = + + = q n n x x p 0.021 396 1 378 1 0.906 0.094 1 1 1 2 ˆ ˆ 1 2  =      =  +         − = + n n  p p pq 计算： 3.12 0.021 ˆ ˆ 0.09392 0.8737 1 2 ˆ ˆ 1 2 = − = − = p − p p p u  因为：u.05=1.96，│u│(3.12)>u0.05，所以p<0.05。 推断：否定H0：p1=p2，接受HA：p1≠p2，即该试验中两块麦 田锈病的发生程度有显著差异。 两个样本百分数相比较的假设测验

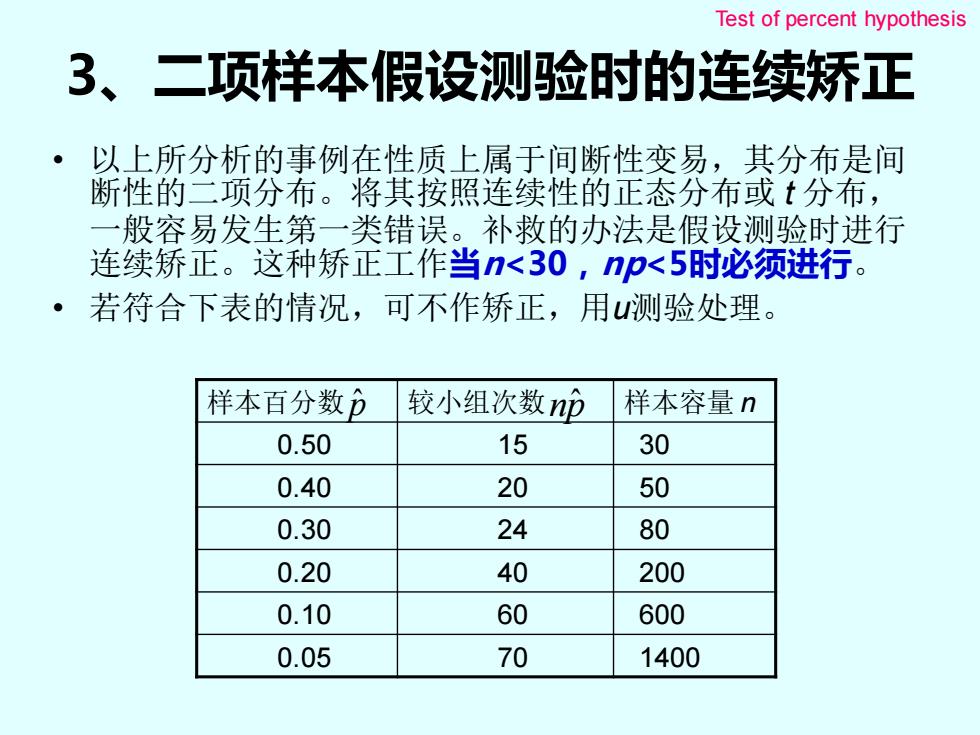
Test of percent hypothesis 3、二项样本假设测验时的连续矫正 以上所分析的事例在性质上属于间断性变易，其分布是间 断性的二项分布。将其按照连续性的正态分布或t分布， 一 般容易发生第一类错误。补救的办法是假设测验时进行 连续矫正。这种矫正工作当n<30,np<5时必须进行。 ·若符合下表的情况，可不作矫正，用u测验处理。 样本百分数p 较小组次数np 样本容量n 0.50 15 30 0.40 20 50 0.30 24 80 0.20 40 200 0.10 60 600 0.05 70 1400

3、二项样本假设测验时的连续矫正 • 以上所分析的事例在性质上属于间断性变易，其分布是间 断性的二项分布。将其按照连续性的正态分布或 t 分布， 一般容易发生第一类错误。补救的办法是假设测验时进行 连续矫正。这种矫正工作当n<30，np<5时必须进行。 • 若符合下表的情况，可不作矫正，用u测验处理。 样本百分数 较小组次数 样本容量 n 0.50 15 30 0.40 20 50 0.30 24 80 0.20 40 200 0.10 60 600 0.05 70 1400 p ˆ np ˆ Test of percent hypothesis

3.1单个样本百分数假设测验的连续矫正 ·单个样本百分数连续校正的计算公式为： Inp-np-0.5 Snp 式中t。为校正后的t值。 Sip =npq Sb是Op=Vnpq 估计值

3.1 单个样本百分数假设测验的连续矫正 • 单个样本百分数连续校正的计算公式为： np c S np np t ˆ ˆ − − 0.5 = 式中 tc 为校正后的 t 值。 Snpˆ = npq np S ˆ 是  npˆ = npq 估计值

单个样本百分数假设测验的连续矫正 ·例题：用基因纯合的糯玉米合非糯玉米杂交，预期F1植株 上糯性花粉粒的po=0.5,现在一个视野中检测20粒花粉， 得糯性花粉8粒，问此结果与理论百分数po=0.5是否相符？ 假设p=p0=0.5,D=8/20=0.4为以随机样本。 即：H0:p=0.5,H≠0.5，=0.05，作两尾测验。 计算：9=1-p=1-0.4=0.6np=ng=20×0.5=10 np=20×0.4=8 ng=20-8=12 SmD=√20×0.4×0.6=2.19 。=8-10-05 0.68 2.19 查附表4：=20-1=19，t0052.093, 计算得|t|<to.o5,故P>0.05, 推断：实得百分数0.4与理论值0.5没有显著差异

• 例题：用基因纯合的糯玉米合非糯玉米杂交，预期F1植株 上糯性花粉粒的p0=0.5，现在一个视野中检测20粒花粉， 得糯性花粉8粒，问此结果与理论百分数p0=0.5是否相符？ 假设 p ˆ p=p0=0.5， =8/20=0.4为以随机样本。 即：H0：p=0.5，HA≠ 0.5， α=0.05，作两尾测验。 计算： q ˆ =1− p =1− 0.4 = 0.6 np = nq = 200.5 =10 np ˆ = 200.4 = 8 nq ˆ = 20 −8 =12 Snpˆ = 200.40.6 = 2.19 0.68 2.19 8 10 0.5 = − − t C = 查附表4：v=20-1=19，t0.05=2.093， 计算得｜t｜< t0.05，故P>0.05， 推断：实得百分数0.4与理论值0.5没有显著差异。 单个样本百分数假设测验的连续矫正