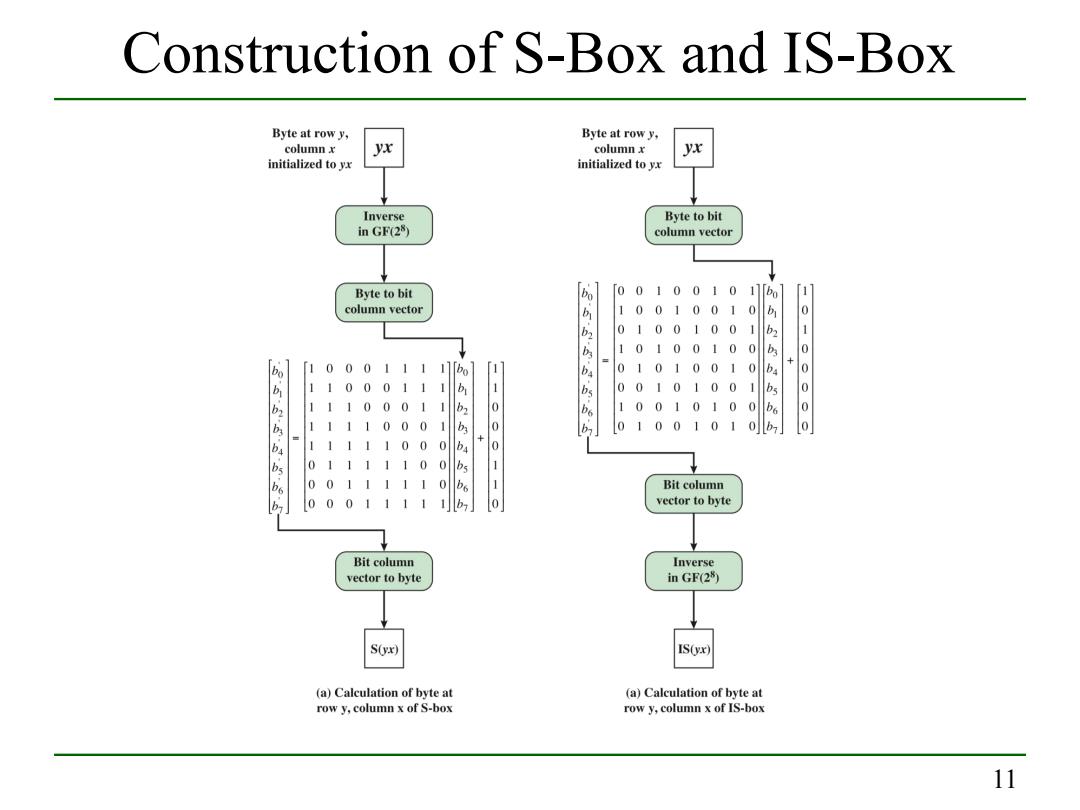
Construction of S-Box and IS-Box Byte at row y, Byte at row y, column x column x initialized to yx initialized to yx Inverse Byte to bit in GF(28) column vector Byte to bit 01001011 bo column vector 1001001 0 01 00100 10 10010 0 [1000111 010 1 001 0 ba 00 b 1100011 0 10100 : 1110001 1000 0 0 01010 0 00 1111000 1 10 0101 0 11 11100 0 0 111110 1 0 011111 0 1 Bit column 0001111 b vector to byte Bit column Inverse vector to byte in GF(28) S(yx) IS(yx) (a)Calculation of byte at (a)Calculation of byte at row y,column x of S-box row y,column x of IS-box 11
11 Construction of S-Box and IS-Box

S-Box rationale The S-box is designed to be resistant to known cryptanalytic attacks The Rijndael developers sought a design that has a low correlation between input bits and output bits and the property that the output is not a linear mathematical function of the input The nonlinearity is due to the use of the multiplicative inverse 12
12 S-Box Rationale The S-box is designed to be resistant to known cryptanalytic attacks The Rijndael developers sought a design that has a low correlation between input bits and output bits and the property that the output is not a linear mathematical function of the input The nonlinearity is due to the use of the multiplicative inverse

Encryption Progress-Shift Rows d4 e0 b8 le Left rotate 0 byte d4 e0 b8 27 bf b4 41 Left rotate 1 byte bf b4 4127 11 985d 52 Left rotate 2 bytes 5d 5211 98 ae fl e5 30 Left rotate 3 bytes 30 ae fl e5 13
13 Encryption Progress – Shift Rows d4 e0 b8 1e 27 bf b4 41 11 98 5d 52 ae f1 e5 30 30 ae f1 e5 d4 e0 b8 1e bf b4 41 27 5d 52 11 98 Left rotate 0 byte Left rotate 1 byte Left rotate 2 bytes Left rotate 3 bytes
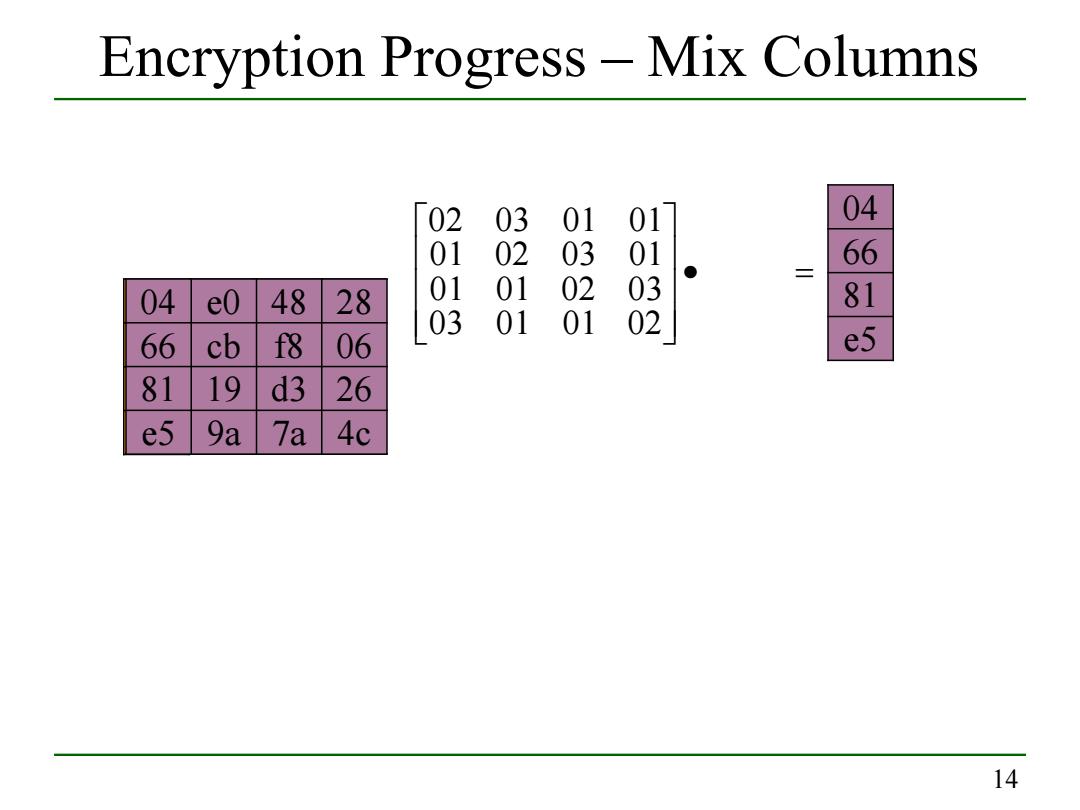
Encryption Progress-Mix Columns 04 66 ● 04 e0 48 28 8888 8200 0320 81 66 cb f8 06 e5 81 19 d3 26 e5 9a 7a 4c 14
14 Encryption Progress – Mix Columns e0 b8 1e b4 41 27 52 11 98 ae f1 e5 d4 bf 5d 30 03 01 01 02 01 01 02 03 01 02 03 01 02 03 01 01 04 66 81 e5 04 e0 48 28 66 cb f8 06 81 19 d3 26 e5 9a 7a 4c

Mix Columns Rationale Coefficients of a matrix based on a linear code with maximal distance between code words ensures a good mixing among the bytes of each column The mix column transformation combined with the shift row transformation ensures that after a few rounds all output bits depend on all input bits 15
15 Mix Columns Rationale Coefficients of a matrix based on a linear code with maximal distance between code words ensures a good mixing among the bytes of each column The mix column transformation combined with the shift row transformation ensures that after a few rounds all output bits depend on all input bits