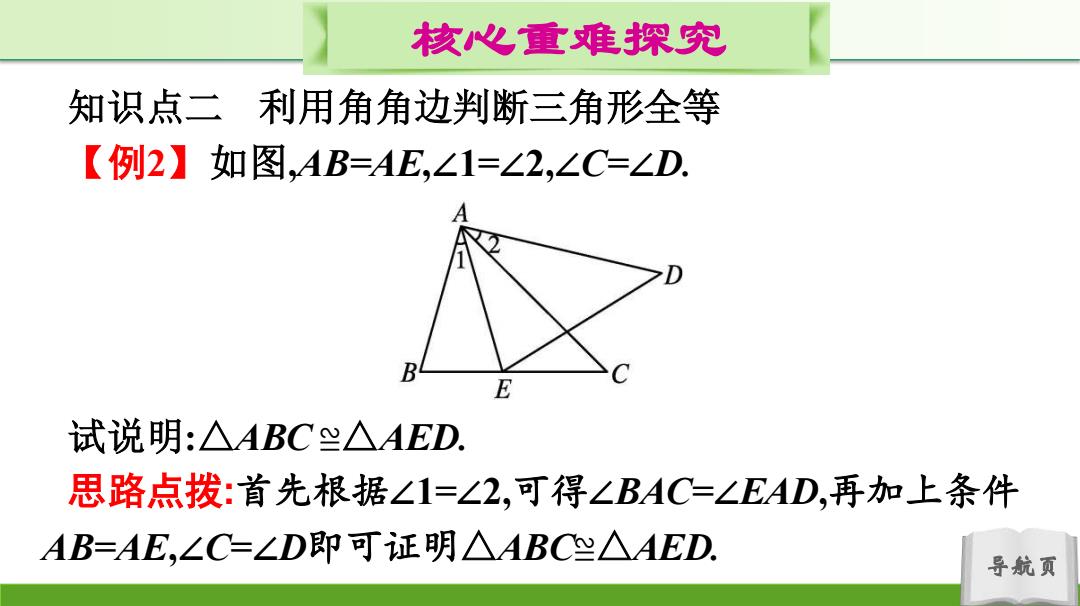
核心重难探究 知识点二利用角角边判断三角形全等 【例2】如图,AB=AE,∠1=∠2,∠C=∠D. B E 试说明:△ABC兰△AED. 思路点拨:首先根据∠1=∠2,可得∠BAC=∠EAD,再加上条件 AB=AE,∠C=∠D即可证明△ABC≌△AED, 导航页
导航页 核心重难探究 知识点二 利用角角边判断三角形全等 【例2】如图,AB=AE,∠1=∠2,∠C=∠D. 试说明:△ABC ≌△AED. 思路点拨:首先根据∠1=∠2,可得∠BAC=∠EAD,再加上条件 AB=AE,∠C=∠D即可证明△ABC≌△AED

核心重难探究 解:.∠1=∠2, '.∠1+∠EAC=∠2+∠EAC, 即∠BAC=∠EAD. (∠D=∠C, '在△ABC和△AED中,}LBAC=∠EAD, (AB=AE, '.△ABC≌△AED(AAS). 【方法归纳】 已经具备条件“两角相等”,判定两个三角形全等若夹边相 等,则用“ASA”;若其中一角的对边相等,则用“AAS”. 导航页
导航页 核心重难探究 解:∵∠1=∠2, ∴∠1+∠EAC=∠2+∠EAC, 即∠BAC=∠EAD. ∵在△ABC 和△AED 中, ∠𝑫 = ∠𝑪, ∠𝑩𝑨𝑪 = ∠𝑬𝑨𝑫, 𝑨𝑩 = 𝑨𝑬, ∴△ABC≌△AED(AAS). 【方法归纳】 已经具备条件“两角相等”,判定两个三角形全等.若夹边相 等,则用“ASA”;若其中一角的对边相等,则用“AAS