
2.杠杆规则 将质量为mR、组成为Xa、 的混合物系R与质量为mE、组成 为ya、y%、的混合物系E相混合 「A 得到一个质量为m、组成为z、 s的新混合物系M,其在三角形坐 标图中分别以点R、E和M表示。 M点称为R点与E点的和点,R点与 Es R E点称为差点。 XA ys 和点M与差点E、R之间的关系 可用杠杆规则描述,即 E (1)几何关系:和点M与差点E、 R共线。即:和点在两差点的连线 B XB ZB YB 上;一个差点在另一差点与和点连 线的延长线上
将质量为mR、组成为xA、xB、 xS的混合物系R与质量为mE、组成 为yA、yB、yS的混合物系E相混合, 得到一个质量为m、组成为zA、zB、 zS的新混合物系M,其在三角形坐 标图中分别以点R、E和M表示。 M点称为R点与E点的和点,R点与 E点称为差点。 和点M与差点E、R之间的关系 可用杠杆规则描述,即 (1)几何关系:和点M与差点E、 R共线。即:和点在两差点的连线 上;一个差点在另一差点与和点连 线的延长线上。 2.杠杆规则

杠杆规则(续) (2)数量关系:和点与差点 A s 的量之间的关系符合杠杆原 理,即, mE- MR XA-ZA XA R mR ME ZA-YA ys mE二 MR _XA一2A mM RE XA-YA mR ME -24-y4 B my RE XB ZB YB 尤A-yA 根据杠杆规则,若已知两个差点,则可确定和点;若已知和 点和一个差点,则可确定另一个差点
杠杆规则(续) (2)数量关系:和点与差点 的量之间的关系符合杠杆原 理,即, a 根据杠杆规则,若已知两个差点,则可确定和点;若已知和 点和一个差点,则可确定另一个差点。 A A A A M R A A A A M E A A A A R E x y z y RE ME m m x y x z RE MR m m z y x z ME MR m m − − = = − − = = − − = =

4.2.2三角形相图 根据萃取操作中各组分的互溶性,可将三元物系 分为以下三种情况, ①溶质A可完全溶于B及S,但B与S不互溶: ②溶质A可完全溶于B及S,但B与S部分互溶: ③溶质A可完全溶于B,但A与S及B与S部分互溶。 习惯上,将①、②两种情况的物系称为第工类物系, 而将③情况的物系称为第Ⅱ类物系。 在萃取操作中,第I类物系较为常见,以下主要讨 论这类物系的相平衡关系
4.2.2 三角形相图 根据萃取操作中各组分的互溶性,可将三元物系 分为以下三种情况, ①溶质A可完全溶于B及S,但B与S不互溶; ②溶质A可完全溶于B及S,但B与S部分互溶; ③溶质A可完全溶于B,但A与S及B与S部分互溶。 习惯上,将①、②两种情况的物系称为第Ⅰ类物系, 而将③情况的物系称为第Ⅱ类物系。 在萃取操作中,第Ⅰ类物系较为常见,以下主要讨 论这类物系的相平衡关系
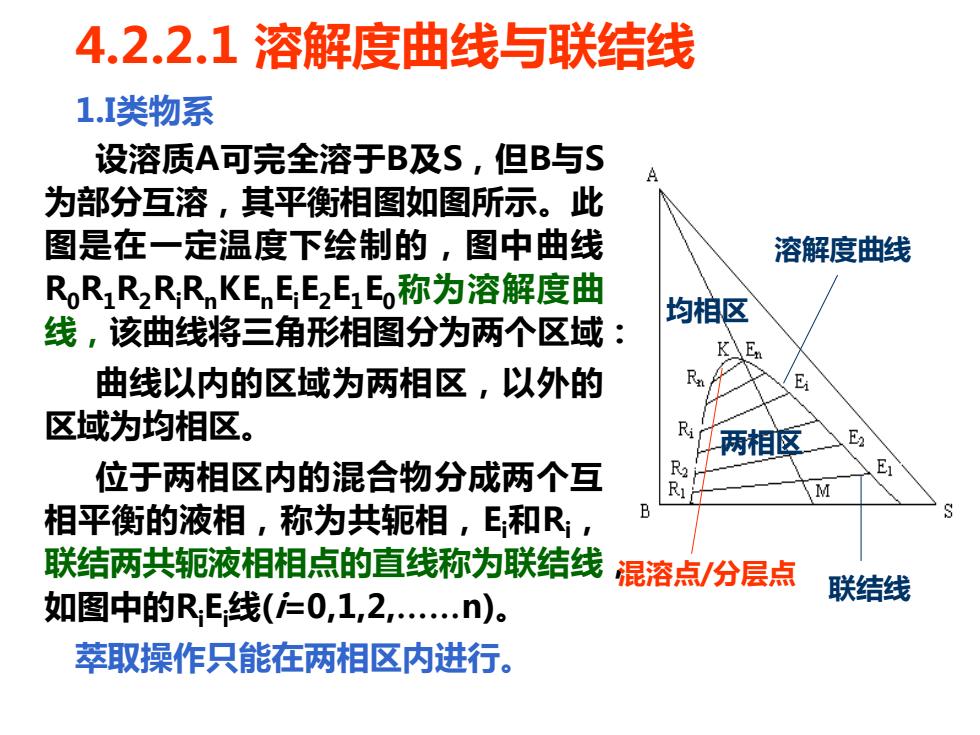
4.2.2.1溶解度曲线与联结线 1.类物系 设溶质A可完全溶于B及S,但B与S 为部分互溶,其平衡相图如图所示。此 图是在一定温度下绘制的,图中曲线 溶解度曲线 R,R1R2 RRKEEE2E1Eo称为溶解度曲 均相区 线,该曲线将三角形相图分为两个区域 K\En 曲线以内的区域为两相区,以外的 E 区域为均相区。 两相区 位于两相区内的混合物分成两个互 R E M 相平衡的液相,称为共轭相,E和R;, 联结两共轭液相相点的直线称为联结线 混溶点/分层点 如图中的RE线(=0,1,2,.n)。 联结线 萃取操作只能在两相区内进行
4.2.2.1 溶解度曲线与联结线 1.I类物系 设溶质A可完全溶于B及S,但B与S 为部分互溶,其平衡相图如图所示。此 图是在一定温度下绘制的,图中曲线 R0R1R2RiRnKEnEiE2E1E0称为溶解度曲 线,该曲线将三角形相图分为两个区域: 曲线以内的区域为两相区,以外的 区域为均相区。 位于两相区内的混合物分成两个互 相平衡的液相,称为共轭相,Ei和Ri, 联结两共轭液相相点的直线称为联结线, 如图中的RiEi线(i=0,1,2,.n)。 萃取操作只能在两相区内进行。 两相区 均相区 溶解度曲线 联结线 混溶点/分层点
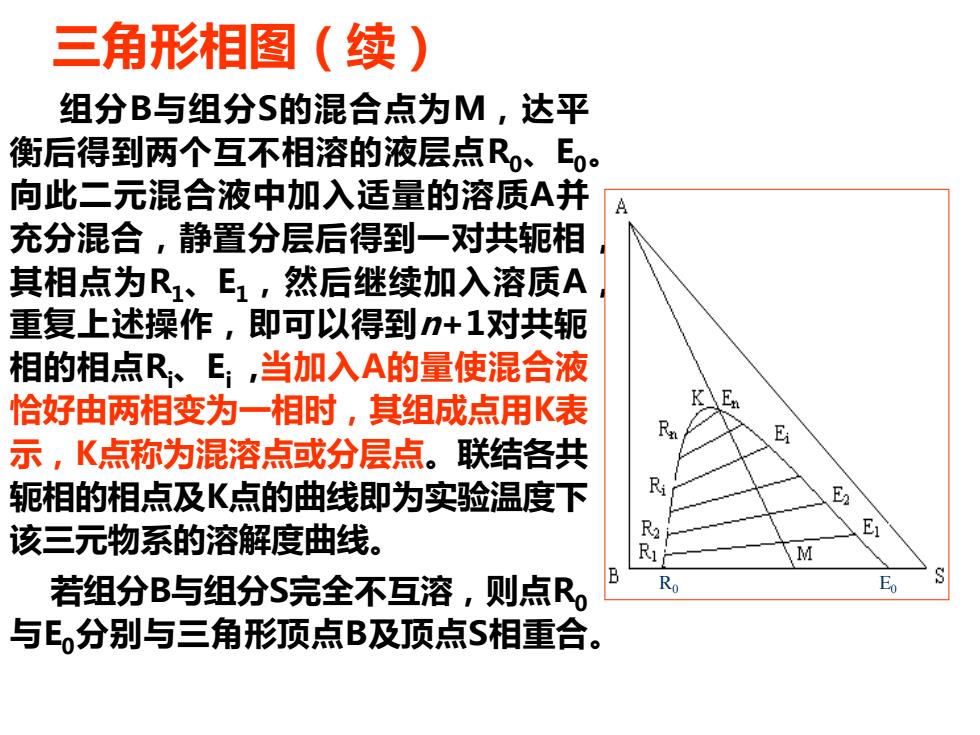
三角形相图(续) 组分B与组分S的混合点为M,达平 衡后得到两个互不相溶的液层点R。、E。 向此二元混合液中加入适量的溶质A并 充分混合,静置分层后得到一对共轭相 其相点为R1、E1,然后继续加入溶质A 重复上述操作,即可以得到n+1对共轭 相的相点R、E,当加入A的量使混合液 恰好由两相变为一相时,其组成点用K表 K En Rn 示,K点称为混溶点或分层点。联结各共 轭相的相点及K点的曲线即为实验温度下 R 该三元物系的溶解度曲线。 R M 若组分B与组分S完全不互溶,则点R, B Ro Eo 与E分别与三角形顶点B及顶点S相重合
三角形相图(续) 组分 B与组分 S的混合点为 M ,达平 衡后得到两个互不相溶的液层点 R 0 、 E 0 。 向此二元混合液中加入适量的溶质 A 并 充分混合 ,静置分层后得到一对共轭相 , 其相点为 R 1 、 E 1 ,然后继续加入溶质 A , 重复上述操作 ,即可以得到 n + 1对共轭 相的相点 R i 、 E i ,当加入 A的量使混合液 恰好由两相变为一相时 ,其组成点用 K表 示 , K点称为混溶点或分层点 。联结各共 轭相的相点及 K点的曲线即为实验温度下 该三元物系的溶解度曲线 。 若组分 B与组分 S完全不互溶 ,则点 R0 与 E 0分别与三角形顶点 B及顶点 S相重合 。 R 0 E 0