
3、给出以下系统函数的并联型实现: # 5.2+1.58z1+1.41z2-1.6z3 1-0.5z)1+0.9z+0.8z 解:对此函数进行因式分解并展成部分分式,得 H日 5.2+1.58z1+1.41z2-1.6z-3 (1-0.5z)1+0.9z1+0.8z2) 0.2 1+0.3z1 =4+ 1-0.5zT1+0.9z1+0.822 0+会子2 [N+H)/2] 则G。=4 1-a2-a C1=0.5 C21=0 a2=-0.9a2=-0.8 =0.2 Y,=0 Yo2=1 72=0.3
3、给出以下系统函数的并联型实现: ( ) ( )( ) 1 2 3 1 1 2 5.2 1.58 1.41 1.6 1 0.5 1 0.9 0.8 z z z H z z z z − − − − − − + + − − + + = 解:对此函数进行因式分解并展成部分分式,得 ( ) ( )( ) 1 2 3 1 1 2 5.2 1.58 1.41 1.6 1 0.5 1 0.9 0.8 z z z H z z z z − − − − − − + + − = − + + 1 1 1 2 0.2 1 0.3 4 1 0.5 1 0.9 0.8 z z z z − − − − + = + + − + + 则 0 G = 4 11 = 0.5 21 = 0 01 = 0.2 11 = 0 12 = −0.9 22 = −0.8 02 =1 12 = 0.3 ( ) ( 1 / 2 ) 1 0 1 0 1 2 1 1 2 1 N k k k k k z H z G z z + − − − = + = + − − 2024/10/21 6
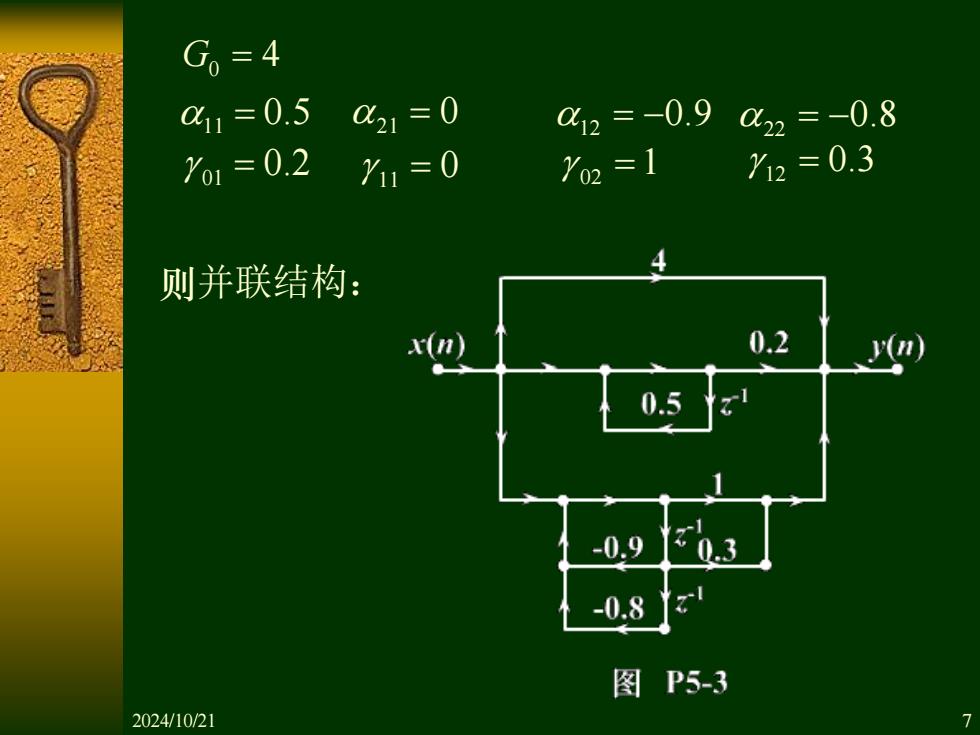
G=4 Cx11=0.5 C21=0 c2=-0.9x2=-0.8 Yo1=0.2711=0 Y2=1 Y12=0.3 则并联结构: x(n) 0.2 0.5 -0.9 0.3 -0.8 图P5-3 2024/10/21
则并联结构: 0 G = 4 11 = 0.5 21 = 0 01 = 0.2 11 = 0 12 = −0.9 22 = −0.8 02 =1 12 = 0.3 2024/10/21 7

1、用横截型结构实现以下系统函数: y0-j0+s0-20-。0- e-0+6:0-2=+&-) -201+6+6g+j0- 20-) =1+1- 8 205 3 2+205 12 一之 2024/10/21 6
4、用横截型结构实现以下系统函数: ( ) ( )( ) ( ) 1 1 1 1 1 1 1 1 1 6 1 2 1 1 2 6 H z z z z z z − − − − − − + − + − = 解: ( ) ( )( ) ( ) 1 1 1 1 1 1 1 1 1 6 1 2 1 1 2 6 H z z z z z z − − − − − − + − + − = ( ) 1 1 1 1 2 1 1 2 1 1 2 1 6 1 2 6 z z z z z z z − − − − − − − − − + + + + − = ( ) 5 37 1 2 1 2 1 1 1 1 2 6 z z z z z − − − − − − + + + − = 8 205 205 8 1 2 3 4 5 1 3 12 12 3 z z z z z − − − − − = + − + − − 2024/10/21 8