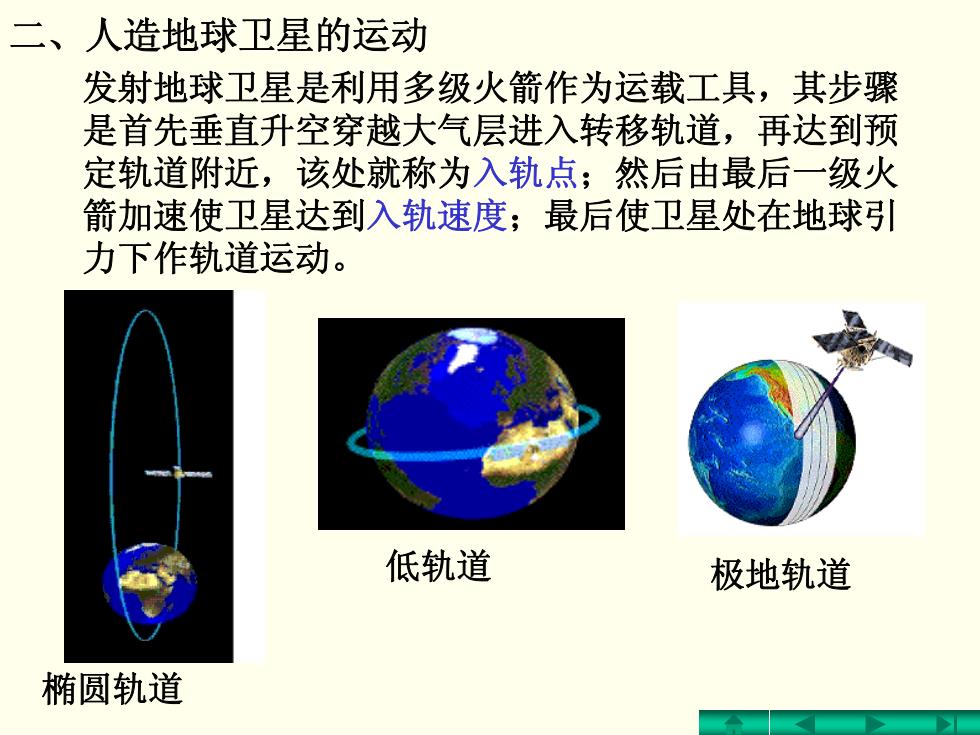
二、人造地球卫星的运动 发射地球卫星是利用多级火箭作为运载工具,其步骤 是首先垂直升空穿越大气层进入转移轨道,再达到预 定轨道附近,该处就称为入轨点;然后由最后一级火 箭加速使卫星达到入轨速度;最后使卫星处在地球引 力下作轨道运动。 低轨道 极地轨道 椭圆轨道
二、人造地球卫星的运动 发射地球卫星是利用多级火箭作为运载工具,其步骤 是首先垂直升空穿越大气层进入转移轨道,再达到预 定轨道附近,该处就称为入轨点;然后由最后一级火 箭加速使卫星达到入轨速度;最后使卫星处在地球引 力下作轨道运动。 椭圆轨道 低轨道 极地轨道

1.地球卫星的轨道 设卫星的入轨点距地心为r,入轨速度为 y,若y垂直于r,m。为地球质量,则当 地球 Gme v二 卫星轨道是以r为半径的圆; V> Gme 卫星轨道是以r为近地点的椭圆; G,卫星轨道是以,为远地点的椭圆。 又若v不垂直于r,则卫星轨道为椭圆,但入轨点既非 近地点也非远地点。令r=R。(地球半径),则得: VI= Gm=、gR=7.9km/s第一字宙速度 1R
1. 地球卫星的轨道 设卫星的入轨点距地心为 r ,入轨速度为 v ,若 v 垂直于 r , me 为地球质量,则当 , e r Gm v = , e r Gm v > , e r Gm v < 卫星轨道是以 r 为半径的圆; 卫星轨道是以 r 为近地点的椭圆; 卫星轨道是以 r 为远地点的椭圆。 地球 v 又若 v 不垂直于 r ,则卫星轨道为椭圆,但入轨点既非 近地点也非远地点。令 r =Re (地球半径),则得: km/s9.7 e e e 1 gR === RGm v 第一宇宙速度

2.地球卫星的轨道参数 在地球引力中,由于角动量守恒,卫星的轨道平面将在空 间保持在某个方位上。为了描述卫星轨道在地心坐标系中 的位形,常引用下列六个轨道参数。 (1)轨道倾角p: 轨道平面与地球赤道面的交角(交线称升交线) p=0°时称为极地轨道(polar orbit); 近地点 (2)升交点赤径0: 升交线与地心春分点连线的夹角; (3)升近角距B: 升交线与近地点矢径的夹角; (4)轨道的半长轴a; 春分点 升交线 (5)偏心率e; (6)经过近地点的时间t
2. 地球卫星的轨道参数 在地球引力中,由于角动量守恒,卫星的轨道平面将在空 间保持在某个方位上。为了描述卫星轨道在地心坐标系中 的位形,常引用下列六个轨道参数。 (1)轨道倾角ϕ : θ β ϕ 近地点 春分点 升交线 ϕ =90˚时称为极地轨道(polar orbit); 轨道平面与地球赤道面的交角(交线称升交线), 升交线与地心-春分点连线的夹角; (3)升近角距 β : 升交线与近地点矢径的夹角; (4)轨道的半长轴 a ; (2)升交点赤径 θ : (5)偏心率 e ; (6)经过近地点的时间 t

若已知卫星的上述六个轨道参数,就可根据开普勒定 律计算卫星在任何时刻所在的位置。考虑到地球的自 转,根据相对运动可列出卫星飞经各地的时间。 3.卫星的轨道设计 根据用途的不同,可将地球卫星分为侦察、导航、通讯、 气象、资料勘探等各种类型。 ·气象卫星为增大观测区域,常采用大轨道倾角; ·为研究地球周围的太空环境,常采用远近地点相差很 大的扁椭圆轨道; ·导航、测距和勘查卫星,常采用近圆形轨道; ·通信卫星,常采用同步轨道。 而卫星的轨道倾角、椭圆偏心率则是由卫星在入轨点的 地理纬度、高度和入轨速度的大小和方向共同决定
若已知卫星的上述六个轨道参数,就可根据开普勒定 律计算卫星在任何时刻所在的位置。考虑到地球的自 转,根据相对运动可列出卫星飞经各地的时间。 3. 卫星的轨道设计 根据用途的不同,可将地球卫星分为侦察、导航、通讯、 气象、资料勘探等各种类型。 • 气象卫星为增大观测区域,常采用大轨道倾角; • 为研究地球周围的太空环境,常采用远近地点相差很 大的扁椭圆轨道 ; • 导航、测距和勘查卫星,常采用近圆形轨道; • 通信卫星,常采用同步轨道。 而卫星的轨道倾角、椭圆偏心率则是由卫星在入轨点的 地理纬度、高度和入轨速度的大小和方向共同决定