
第9章热力学定律 §9.1内能功和热量 准静态过程 §9.2热力学第一定律热容 §9.3绝热过程多方过程 §9.4循环过程卡诺循环过程 §9.5热力学第二定律 §9.6热力学过程的不可逆性 §9.7热力学系统的熵 §9.8熵增加原理 §9.9热力学第二定律的统计意义 熵的统计表述有序和无序
§9.1 内能 功和热量 准静态过程 第 9 章 热力学定律 §9.2 热力学第一定律 热容 §9.3 绝热过程 多方过程 §9.5 热力学第二定律 §9.6 热力学过程的不可逆性 §9.7 热力学系统的熵 §9.8 熵增加原理 §9.9 热力学第二定律的统计意义 熵的统计表述 有序和无序 §9.4 循环过程 卡诺循环过程
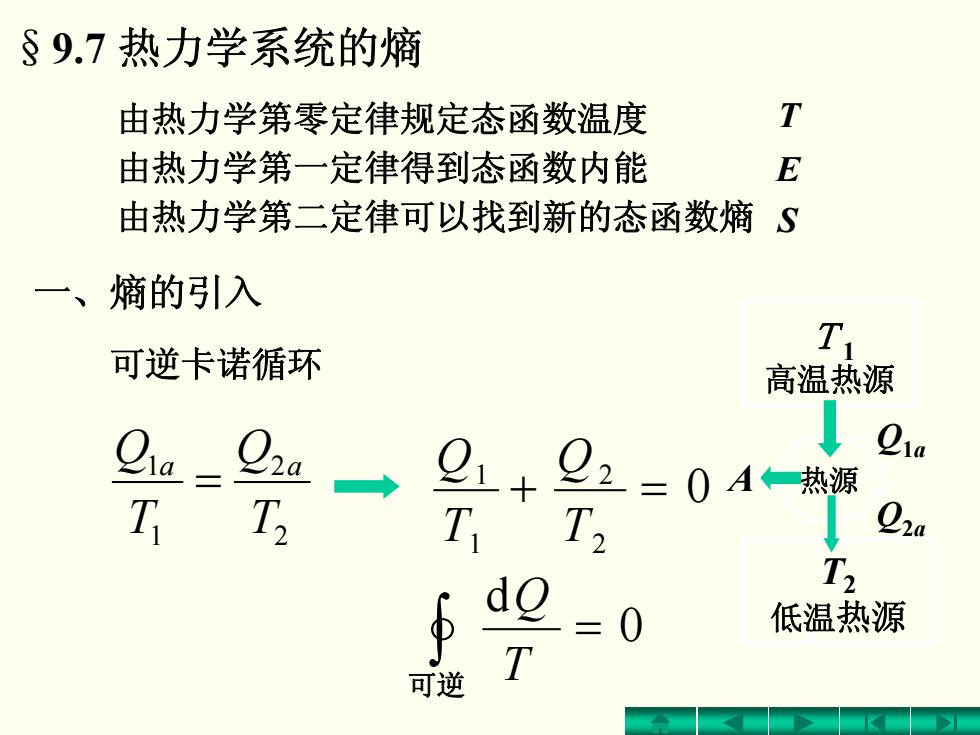
§9.7热力学系统的熵 由热力学第零定律规定态函数温度 T 由热力学第一定律得到态函数内能 E 由热力学第二定律可以找到新的态函数熵S 一、熵的引入 可逆卡诺循环 T 高温热源 22a ↓ 1 21a T T 2=0A一 T T, 22a do T 低温热源 T 可逆
由热力学第零定律规定态函数温度 T 一、熵的引入 可逆卡诺循环 0 2 2 1 1 =+ T Q T Q 2 2 1 1 T Q T Q aa = ∫ = 可逆 0 d T Q §9.7 热力学系统的熵 T 1 高温热源 T2 低温热源 A 热源 Q 1 a Q 2 a 由热力学第一定律得到态函数内能 E 由热力学第二定律可以找到新的态函数熵 S

任一可逆循环(图示) 绝热线 可以看作由许多微小卡 诺循环拼成,相邻两个 等温线 微小卡诺循环因过程相 反而大部分抵消,留下 一个锯齿形曲线一用 来近似替代可逆循环。 0 V 任一微小卡诺循环 02=0 Ta
可以看作由许多微小卡 诺循环拼成,相邻两个 微小卡诺循环因过程相 反而大部分抵消,留下 一个锯齿形曲线—— 用 来近似替代可逆循环。 任一可逆循环(图示) o V p 等温线 绝热线 任一 微小卡诺循环 Qi1 Qi2 Ti1 Ti2 0 2 2 1 1 =+ i i i i T Q T Q

所有微小卡诺循环叠加 无限细分锯齿曲线无限接近原来的可逆循环 do 入 克劳修斯等式 可逆 设可逆循环12b1 p 9鸭+兴=0 1 L 0 V
所有微小卡诺循环叠加 ∑ = 0 i i i T Q 无限细分锯齿曲线无限接近原来的可逆循环 ∫ = 可逆 0 d T Q 克劳修斯等式 设可逆循环 1 a 2 b 1 0 dd 21 12 =+= a ∫∫ b T Q T Q ∫ T d Q p o V 1 2 a b

J1b2 T 表明沿可逆过程的 d9的积分,只取决于始末状 态,而与过程无关。因此可以认为存在一个新的态函 数,克劳修斯称这个态函数为“熵”。 定义状态函数S: 52-8,=[2 T 可逆 9=2+9=0 0
定义状态函数 S: ∫ =− 21 12 dTQ SS 可逆 表明沿可逆过程的 的积分,只取决于始末状 态,而与过程无关。因此可以认为存在一个新的态函 数,克劳修斯称这个态函数为“熵”。 T dQ ∫∫ = 21 21 dd a b TQ TQ p o V 1 2 a b 0 dd 21 12 =+= a ∫∫ b TQ TQ ∫ TdQ