
b1:b=4; ni a1:a=b+c; d:d=a*b; n3 c1:c=b+c; 5 d2:d=a+b; n2 b2:b=a-c; c2:c=a*b; 7n4 f(a-b); 6 f(b+c); n7 8(a+b); Var la,b,c,d) Defs (a1,b1,b2,c1,c2,di,d2 h(a-c); Expr=la*b,a+b,a-b,a-c,b+c) 8 f(b+c);
13

Analysis:Available Expressions An expression e is available at program point p if >e is computed on every path to p,and the value of e has not changed since the last time e was computed on every path to p Optimization If an expression is available,need not be recomputed -(At least,if it is still in a register somewhere) 14
Analysis: Available Expressions An expression e is available at program point p if ➢ e is computed on every path to p, and ➢ the value of e has not changed since the last time e was computed on every path to p Optimization If an expression is available, need not be recomputed - (At least, if it is still in a register somewhere) 14

Available Expressions Example:An expression,x+y,is available at node n if every path from the entry node to n evaluates x+y,and there are no definitions of x or y after the last evaluation entry .x+y.. x and y not defined .x+y. along blue edges 15
Available Expressions • Example: An expression, x+y, is available at node n if every path from the entry node to n evaluates x+y, and there are no definitions of x or y after the last evaluation 15
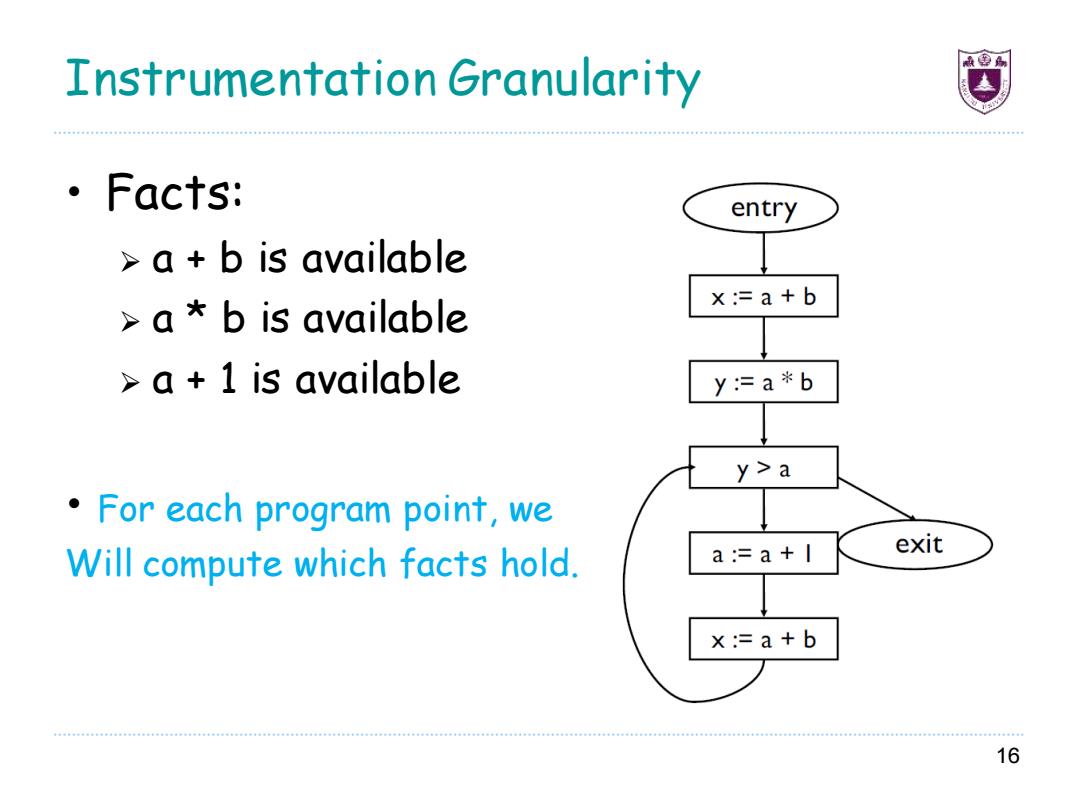
Instrumentation Granularity ·Facts: entry a b is available x:=a+b a b is available a 1 is available y:=a*b y>a For each program point,we exit Will compute which facts hold. a:=a+| x:=a+b 16
Instrumentation Granularity • Facts: ➢ a + b is available ➢ a * b is available ➢ a + 1 is available • For each program point, we Will compute which facts hold. 16

Gen and Kill Assumption At most one definition per node -We can refer to definitions by their node "number" Gen[n]:Definitions that are generated by node n(at most one) Kill[n]:Definitions that are killed by node n 17
Gen and Kill 17