
NANJING UNIVERSITY Turing Machine Turing Machines Recursive and Recursively Enumerable Languages .1
Turing Machines Recursive and Recursively Enumerable Languages Turing Machine 1

效绵鼎 Turing-Machine Theory The purpose of the theory of Turing machines is to prove that certain specific languages s have no algorithm. Start with a language about Turing machines themselves. ■ Reductions are used to prove more common questions undecidable 2
Turing-Machine Theory ◼ The purpose of the theory of Turing machines is to prove that certain specific languages have no algorithm. ◼ Start with a language about Turing machines themselves. ◼ Reductions are used to prove more common questions undecidable. 2
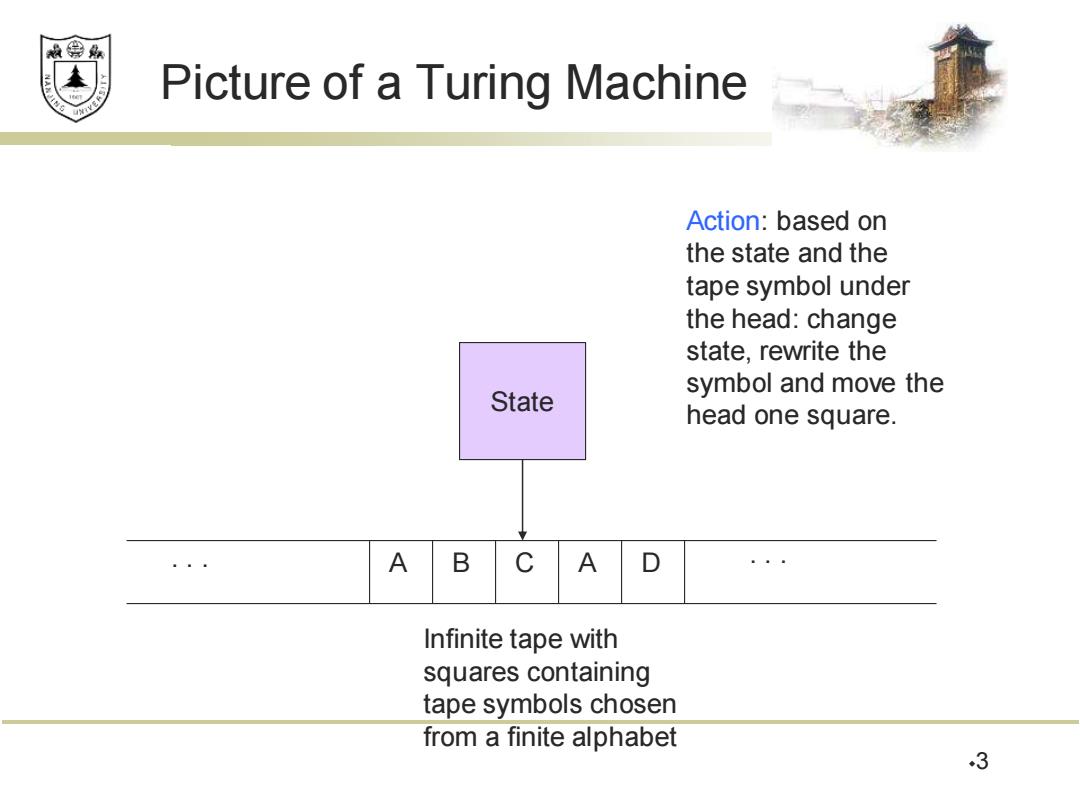
效绵 Picture of a Turing Machine Action:based on the state and the tape symbol under the head:change state,rewrite the symbol and move the State head one square. A B C A D Infinite tape with squares containing tape symbols chosen from a finite alphabet 3
Picture of a Turing Machine 3 State . . . A B C A D . . . Infinite tape with squares containing tape symbols chosen from a finite alphabet Action: based on the state and the tape symbol under the head: change state, rewrite the symbol and move the head one square

效绵鼎 Why Turing Machines? Why not deal with C programs or something like that? Answer:You can,but it is easier to prove things about TM's,because they are so simple. o And yet they are as powerful as any computer. More so,in fact,since they have infinite memory. 4
Why Turing Machines? ◼ Why not deal with C programs or something like that? ◼ Answer: You can, but it is easier to prove things about TM’s, because they are so simple. And yet they are as powerful as any computer. ◼ More so, in fact, since they have infinite memory. 4

效绵鼎 Turing-Machine Formalism A TM is described by: 1.A finite set of states (Q,typically). 2.An input alphabet(Σ,typically) 3.A tape alphabet (T,typically;contains >) 4. A transition function(δ,typically)) 5. A start state (qo,in Q,typically). 6. A blank symbol(B,in「-Σ,typically). u All tape except for the input is blank initially. 7. A set of final states (F Q,typically) 5
Turing-Machine Formalism ◼ A TM is described by: 1. A finite set of states (Q, typically). 2. An input alphabet (Σ, typically). 3. A tape alphabet (Γ, typically; contains Σ). 4. A transition function (δ, typically). 5. A start state (q0 , in Q, typically). 6. A blank symbol (B, in Γ- Σ, typically). u All tape except for the input is blank initially. 7. A set of final states (F ⊆ Q, typically). 5