
必做作业SDI补:将下列复数补:将下列复数化化为极坐标形式为代数形式F= 10 Z-73°Fi=-5-j5部资料!F-122152°F2=15 Z 112.6°F2=-4+j3正F3=20+j40F4-10 Z-90°F4=j10请Fs=5/-180°Fs=-3F-10 2/13 !F=2.78+j9.216
SDUT 内 部 资 料! 请 勿 外 传! 必做作业 16 补:将下列复数 化为极坐标形式 补:将下列复数化 为代数形式 F1=-5-j5 F2=-4+j3 F3=20+j40 F4=j10 F5=-3 F6=2.78+j9.2 F1= 10∠-73° F2=15∠112.6° F3=1.2∠152° F4=10∠-90° F5=5∠-180° F6=10∠-135°

必做作业补:计算,并化为极坐标形式1.F=10 Z—60°·j52.F2=-j5 : 4Z -53补:计算,并化为代数形式内一部4.F =1+3.F, = j2 +资料!1-i2补:计算,并化为极坐标形式6.F=20 Z30°-j205.F, = 5/2Z-45°+10Z90°习题8-6- 求[F;+F2|最小时的F1。17
SDUT 内 部 资 料! 请 勿 外 传! 必做作业 17 补:计算,并化为极坐标形式 j j F j - - = + 1 . 2 3 3 j j F - + + = + 1 2 1 1 1 4. 4 1 1.F1=10∠-60°· j5 2.F2= -j5 · 4∠-53 补:计算,并化为代数形式 5. = 5 2 - 45 + 1090 F5 补:计算,并化为极坐标形式 6.F6=20∠30°-j20 F1 = |F1 |60 ,F2 = -7.07 - j7.07 求 |F1+F2 |最小时的F1。 习题8-6

S 8-2 正弦量电路中按正弦规律变化的电压或电流,统称正弦量。研究正弦电路的意义是正弦交流电有很多优点,使它应用广泛。例如:①可以根据需要,利用变压器方便地把正弦电压升高“资料或降低;②电机、变压器等电气设备;石在正弦交流电下具有较好的性能;③正弦量对时间的导数、积分、几个同频率正弦量的加减,其结果仍是同频率的正弦量,这不仅使电路的分析计算变得简单,而且其结果还可以推广到非正弦传!周期电流电路中
SDUT 内 部 资 料! 请 勿 外 传! §8-2 正弦量 电路中按正弦规律变化的电压或电流,统称正弦量。 研究正弦电路的意义是正弦交流电有很多优点,使它应用广 泛。例如: ①可以根据需要,利用变压器方便地把正弦电压升高 或降低; ②电机、变压器等电气设备,在正弦交流电下具有较 好的性能; ③正弦量对时间的导数、积分、几个同频率正弦量的 加减,其结果仍是同频率的正弦量,这不仅使电路的 分析计算变得简单,而且其结果还可以推广到非正弦 周期电流电路中

S综上:对正弦电路的分析研究具有重要的理论价值和实际意义。正弦量的时域表达式有两种形式i = Imcos(ot+d)内部;要msin(a+)也称为瞬时值表达式分析时不可混用,以免发生相位错误今后采用的形式以教材为准1- %.cos(at+g.)i = Imcos(ot+Φ)传!19
SDUT 内 部 资 料! 请 勿 外 传! 19 i = Imcos(wt+i) i = Imsin(wt+i) 也称为瞬时值表达式 分析时不可混用,以免发生相位错误。 今后采用的形式以教材为准: i = Imcos(wt+i) u = Umcos(wt+u ) 综上:对正弦电路的分析研究具 有重要的理论价值和实际意义。 正弦量的时域表达式有两种形式
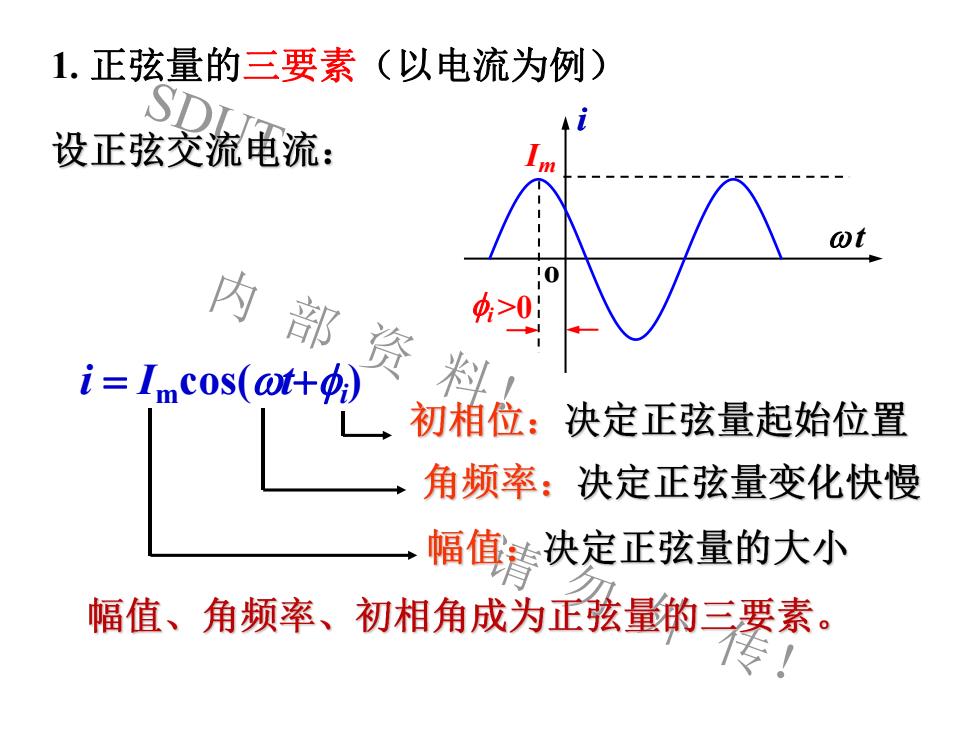
1.正弦量的三要素(以电流为例SDU设正弦交流电流:mot:0内部资料Φ;>0:i = Imcos(ot+Φ)初相位:决定正弦量起始位置角频率:决定正弦量变化快慢幅值主决定正弦量的大小幅值、角频率、初相角成为正弦量的三要素。传!
SDUT 内 部 资 料! 请 勿 外 传! 1. 正弦量的三要素(以电流为例) i = Imcos(wt+i) o i w t i>0 i Im