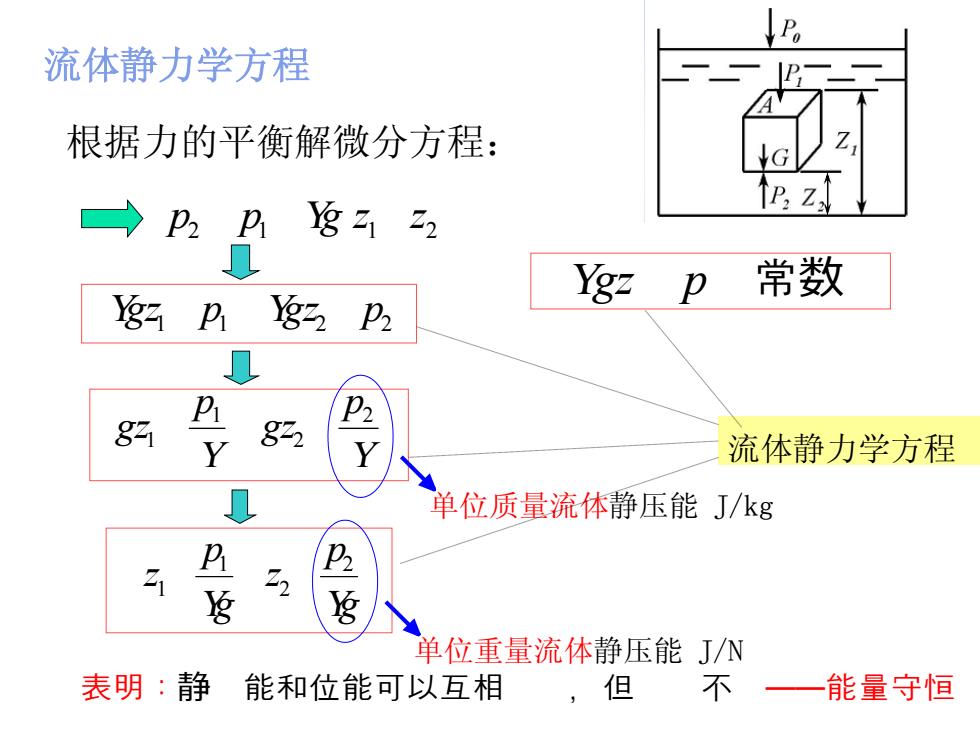
流体静力学方程 根据力的平衡解微分方程: P,Z zp常数 1p2P2 L 85 Y 822 流体静力学方程 单位质量流体静压能J/kg P P Z 22 g 单位重量流体静压能J/N 表明:静 能和位能可以互相 ,但 不一 能量守恒
gz p 常数 流体静力学方程 流体静力学方程 根据力的平衡解微分方程: 2 1 1 2 p p g z z g p z g p z 2 2 1 1 1 1 2 2 gz p gz p 2 2 1 1 p gz p gz 单位质量流体静压能 J/kg 表明:静 能和位能可以互相��,但��不 ——能量守恒 单位重量流体静压能 J/N
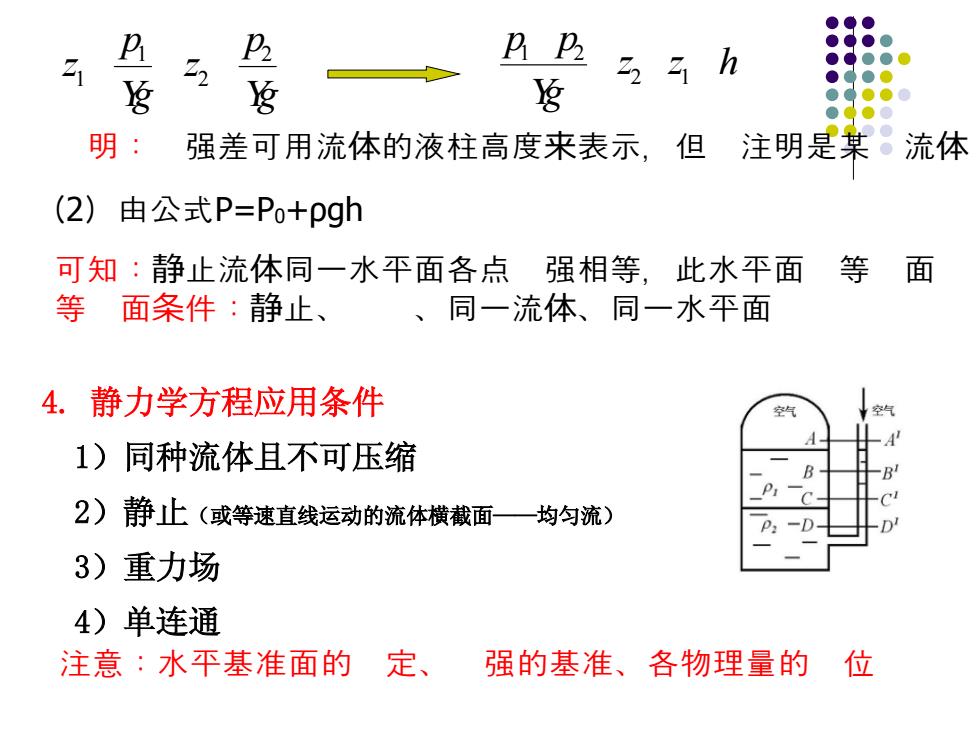
P P A凸 33h g g g 明: 强差可用流体的液柱高度来表示,但 注明是某 流体 (2)由公式P=Po+pgh 可知:静止流体同一水平面各点强相等,此水平面 等 面 等 面条件:静止、 、同一流体、同一水平面 4.静力学方程应用条件 1)同种流体且不可压缩 2)静止(或等速直线运动的流体横截面一均匀流) 3)重力场 4)单连通 注意:水平基准面的 定、 强的基准、各物理量的 位
4. 静力学方程应用条件 1)同种流体且不可压缩 2)静止(或等速直线运动的流体横截面——均匀流) 3)重力场 4)单连通 g p z g p z 2 2 1 1 z z h g p p 2 1 1 2 明: 强差可用流体的液柱高度来表示,但 注明是某 流体 (2)由公式P=P0+ρgh 可知:静止流体同一水平面各点 强相等,此水平面 等 面 等 面条件:静止、��、同一流体、同一水平面 注意:水平基准面的 定、 强的基准、各物理量的 位

1.2.2流体的总势能 总势能(压强能与位能之和) 虚拟压强 P=p+pgt
1.2.2 流体的总势能 总势能 (压强能与位能之和) 虚拟压强
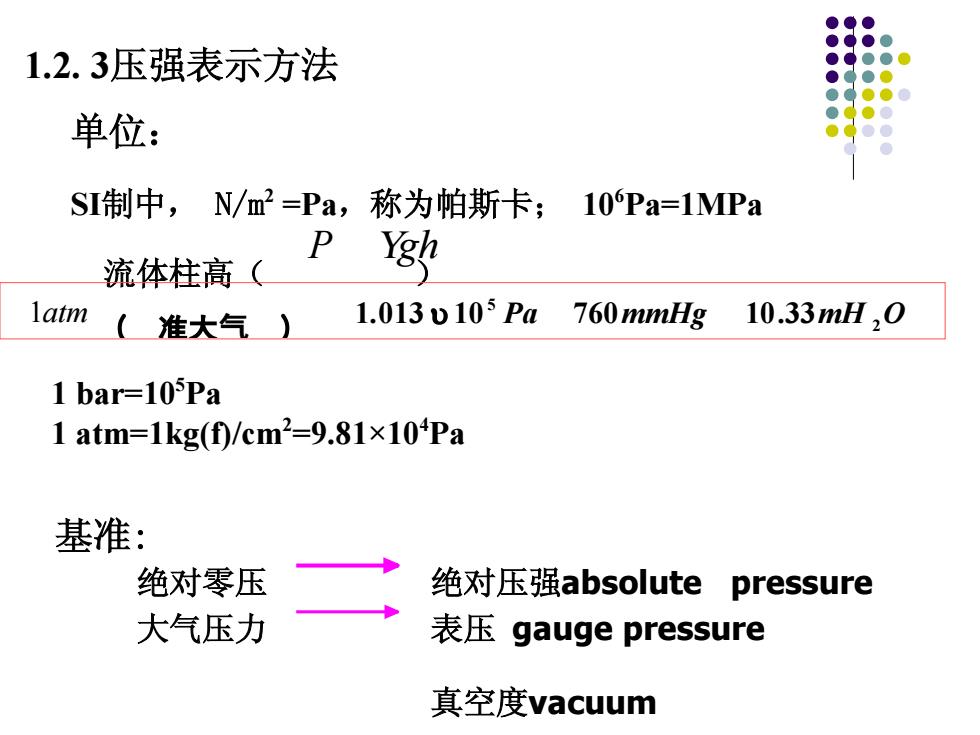
1.2.3压强表示方法 单位: SI制中,N/m2=Pa,称为帕斯卡; 10Pa=1MPa P 流体柱高( g latm (准大气)】 1.013o105Pa760mmHg 10.33mlH,0 1 bar=105Pa 1atm=1kg(f/cm2=9.81×104Pa 基准: 绝对零压 绝对压强absolute pressure 大气压力 表压gauge pressure 真空度vacuum
1.2. 3压强表示方法 单位: SI制中, N/m2 =Pa,称为帕斯卡; 106 Pa=1MPa 流体柱高( ) 1atm (�准大气�) Pa mmHg mH 2O 5 1.013 10 760 10.33 P gh 基准: 绝对零压 绝对压强absolute pressure 大气压力 表压 gauge pressure 真空度vacuum 1 bar=105 Pa 1 atm=1kg(f)/cm2 =9.81×104 Pa
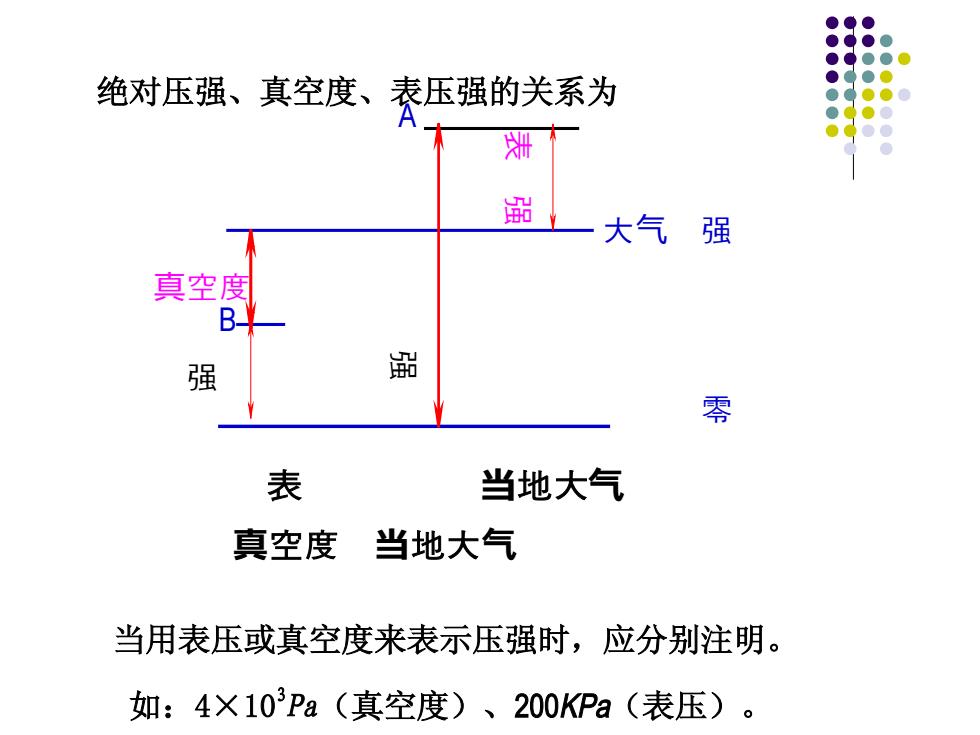
绝对压强、真空度、表压强的关系为 知 删 大气 强 真空度 B 强 品 零 表 当地大气 真空度 当地大气 当用表压或真空度来表示压强时,应分别注明。 如:4×103Pa(真空度)、200KPa(表压)
绝对压强、真空度、表压强的关系为 ��零�� 大气 强 A 强 表 强 B ���强 真空度 当用表压或真空度来表示压强时,应分别注明。 如:4×103 Pa(真空度)、200KPa(表压)。 表� ��当地大气� 真空度 当地大气� ��