《化工原理》课程教学资源（课件讲稿）第1章 流体流动及总结（Fluid flow）

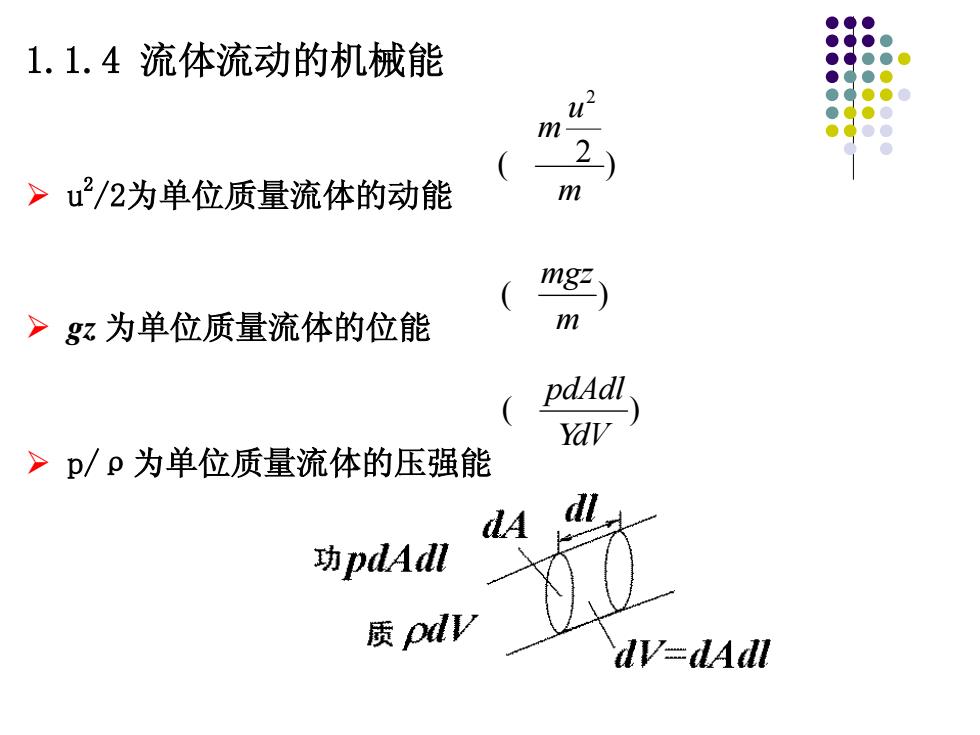
1.1.4流体流动的机械能 >u2/2为单位质量流体的动能 >gz为单位质量流体的位能 m pdAdl >p/p为单位质量流体的压强能 A 功odAdl dV=dAdl

1.1.4 流体流动的机械能 u2  /2为单位质量流体的动能  gz 为单位质量流体的位能  p/ρ为单位质量流体的压强能 ) 2 ( 2 m u m ( ) m mgz ( ) dV pdAdl 

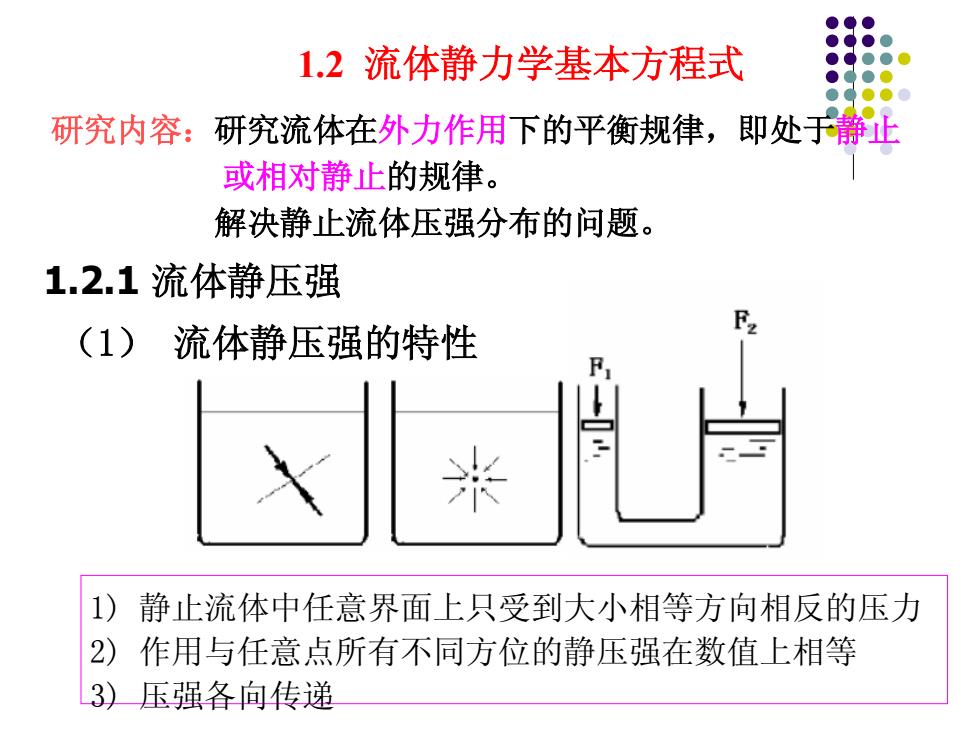
1.2流体静力学基本方程式 研究内容：研究流体在外力作用下的平衡规律，即处于静止 或相对静止的规律。 解决静止流体压强分布的问题。 1.2.1流体静压强 F, (1) 流体静压强的特性 F 米 1) 静止流体中任意界面上只受到大小相等方向相反的压力 2)作用与任意点所有不同方位的静压强在数值上相等 3)压强各向传递

1.2 流体静力学基本方程式 研究内容：研究流体在外力作用下的平衡规律，即处于静止 或相对静止的规律。 解决静止流体压强分布的问题。 1.2.1 流体静压强 （1） 流体静压强的特性 1) 静止流体中任意界面上只受到大小相等方向相反的压力 2) 作用与任意点所有不同方位的静压强在数值上相等 3) 压强各向传递

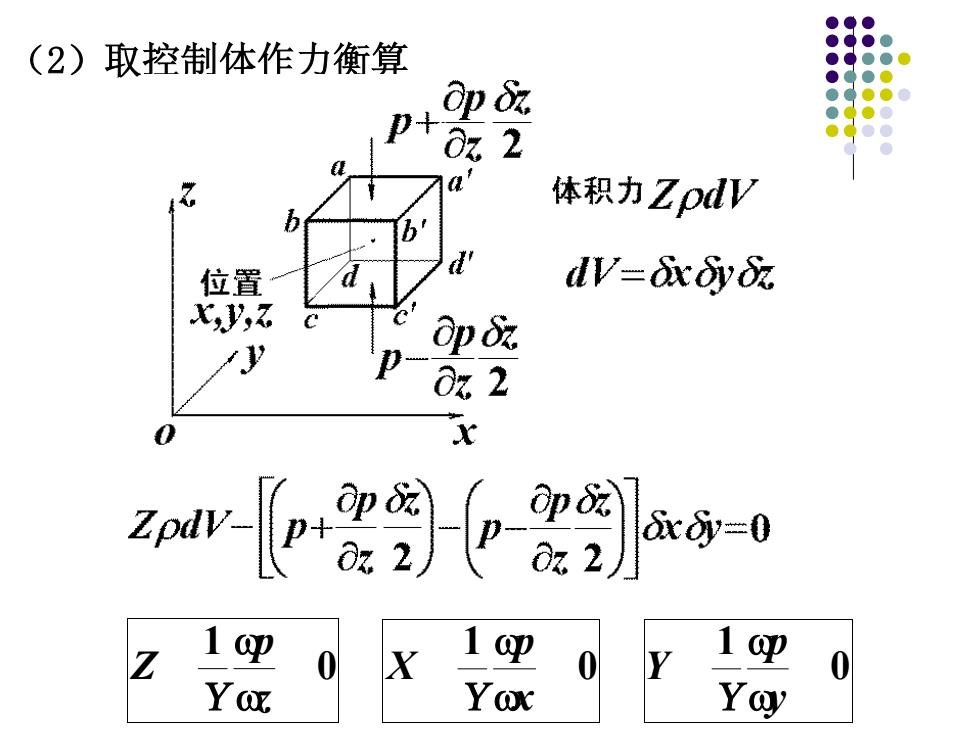
(2)取控制体作力衡算 op 0z2 体积力ZpdV 位置 dV-oxoy ,Z Op &r. 0z2 X zwre-ia0 0 X 0 0 Y Yox Yay

（2）取控制体作力衡算 0 1     z p Z  0 1     x p X  0 1     y p Y 

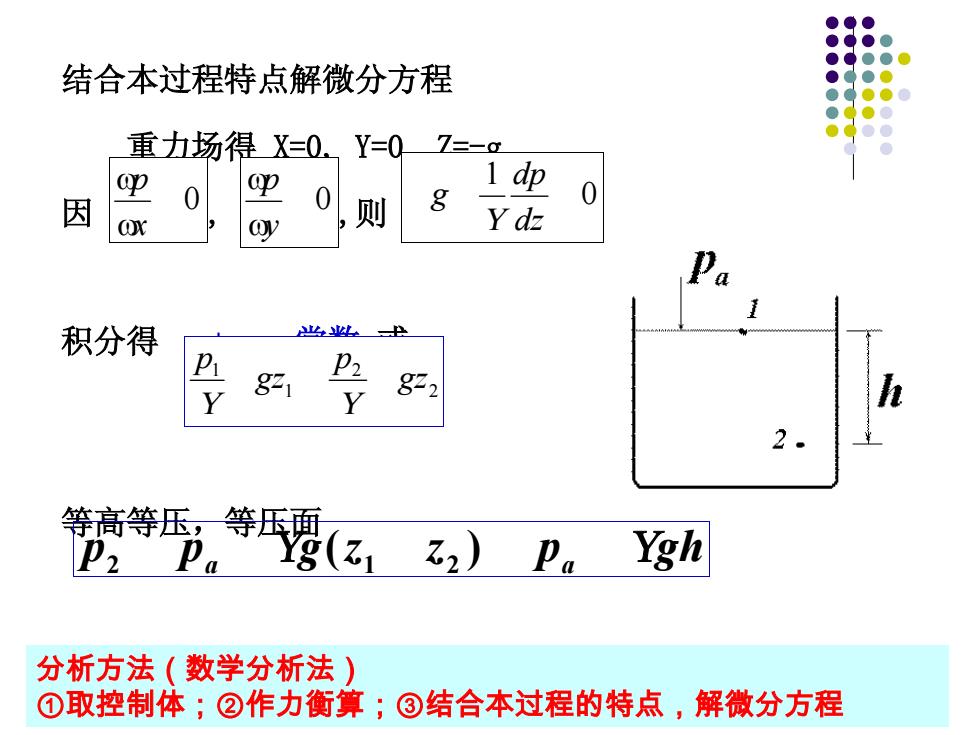
结合本过程特点解微分方程 重力场得X=0.Y=0 7=-a ap 1 dp ( 因 则 8 Ydz 积分得 以n P 821 P2 822 29 等高等等压碧(21乙2卫。g p2卫a 分析方法（数学分析法） ①取控制体；②作力衡算；③结合本过程的特点，解微分方程

结合本过程特点解微分方程 重力场得 X=0, Y=0, Z=-g 因 , ,则 积分得 p+ρgz=常数 或 等高等压，等压面 0   x p 0   y p 0 1 dz dp g  2 2 1 1 gz p gz p   p2  pa  g(z1  z2 )  pa  gh 分析方法（数学分析法） ①取控制体；②作力衡算；③结合本过程的特点，解微分方程

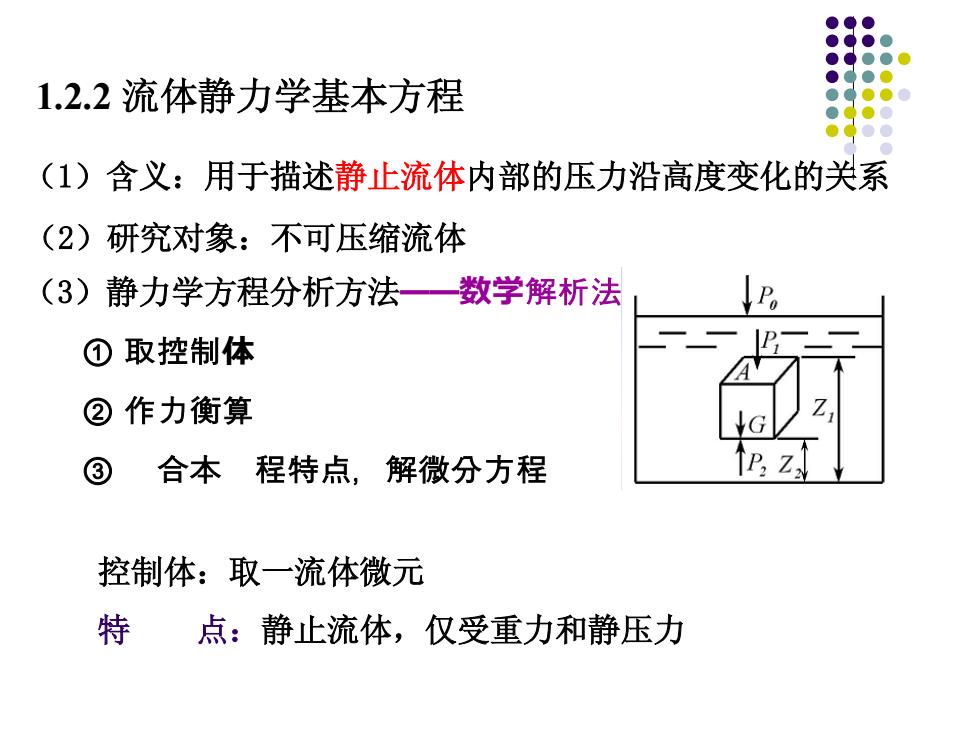
1.2.2流体静力学基本方程 (1)含义：用于描述静止流体内部的压力沿高度变化的关系 (2)研究对象：不可压缩流体 (3)静力学方程分析方法—数学解析法 ①取控制体 ②作力衡算 ③ 合本 程特点，解微分方程 22 控制体：取一流体微元 特点：静止流体，仅受重力和静压力

1.2.2 流体静力学基本方程 （1）含义：用于描述静止流体内部的压力沿高度变化的关系 （2）研究对象：不可压缩流体 （3）静力学方程分析方法——数学解析法 ① 取控制体 ② 作力衡算 ③ �合本�程特点，解微分方程 控制体：取一流体微元 特 点：静止流体，仅受重力和静压力