
时变电磁场边界条件 。电场法向边界条件 。电通量 ∮,D.a5=D-(AS+D,nAS=(D,-D)-nAs ● 如果分界面的薄层内有自由电荷,则圆柱面内包围的总 电荷为 =pdv=lim phAS=PsAS h→0 。由高斯定理 (D-D)=Ps lexu@mail.xidian.edu.cn Dan-Din Ps
时变电磁场边界条件 电场法向边界条件 电通量 如果分界面的薄层内有自由电荷,则圆柱面内包围的总 电荷为 由高斯定理 lexu@mail.xidian.edu.cn 7 1 2 21 () ( ) ˆˆˆ S D dS D Sn D n S D D n S ⋅ = ⋅ −∆ + ⋅ ∆ = − ⋅ ∆ ∫ ∫ ∆=∆== V → S h ρρρ SShdVQ 0 lim 2 1 ˆ ( ) S nD D ⋅−= ρ D D 2 1 n nS − = ρ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

时变电磁场边界条件 ●若分界面上无自由面电荷 Din D2n Ein E2E2n 分界面上有自由面电荷,电位移矢量D法向分量D不连 续,有一等于面电荷密度ps的突变; ●分界面上无自由面电荷,则电位移矢量D法向分量D,连 续 ·分界面两侧的电场强度矢量的法向分量E,一般不连续。 lexu@mail.xidian.edu.cn
时变电磁场边界条件 若分界面上无自由面电荷 分界面上有自由面电荷,电位移矢量D法向分量Dn不连 续,有一等于面电荷密度ρS的突变; 分界面上无自由面电荷,则电位移矢量D法向分量Dn连 续; 分界面两侧的电场强度矢量的法向分量En一般不连续。 lexu@mail.xidian.edu.cn 8 = DD 21 nn n EE 2211 n = εε XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

时变电磁场边界条件 。磁场法向边界条件 。由磁通连续性原理 i(B2-B)=0 Bin Ban 。由本构关系可知 Hn=M2H2n lexu@mail.xidian.edu.cn
时变电磁场边界条件 磁场法向边界条件 由磁通连续性原理 由本构关系可知 lexu@mail.xidian.edu.cn 9 2 1 nB B ˆ ⋅−= ( )0 = BB 21 nn n = µµ HH 2211 n XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
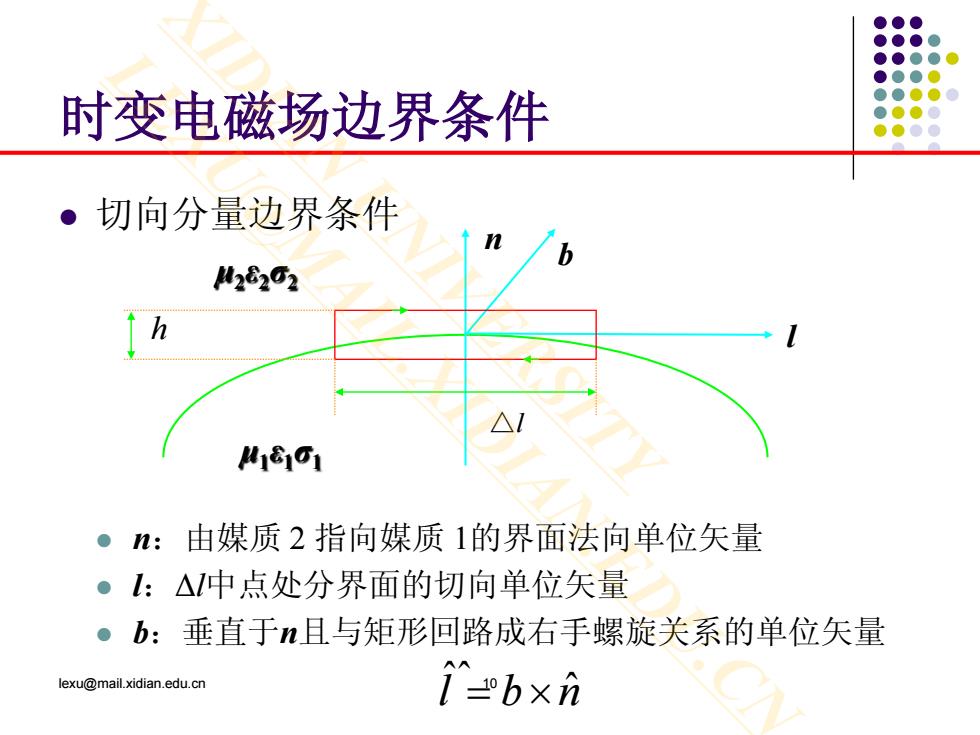
时变电磁场边界条件 ·切向分量边界条件 4282G2 4181C1 ●n:由媒质2指向媒质1的界面法向单位矢量 。:△中点处分界面的切向单位矢量 。b:垂直于n且与矩形回路成右手螺旋关系的单位矢量 lexu@mail.xidian.edu.cn 1=bxn
时变电磁场边界条件 切向分量边界条件 n:由媒质 2 指向媒质 1的界面法向单位矢量 l:Δl中点处分界面的切向单位矢量 b:垂直于n且与矩形回路成右手螺旋关系的单位矢量 lexu@mail.xidian.edu.cn 10 μ1ε1σ1 μ2ε2σ2 n b h l △l ˆˆ l bn = × ˆ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

时变电磁场边界条件 ● 电场切向边界条件 。考虑麦克斯韦方程组推广的法拉第电磁感应定律 ∮,Ed aB ds 。积分回路上的积分结果 ∮Edi=E(-1)A1+E,1=1(E2-E)A1 =bx(E2-E)△1=b·n×(E2-E)A1 ·面积分结果 oB aB 6hA1=0 h-0 Ot 切向边界条件 lexu@mail.xidian.edu.cn n×(E2-E)=0
时变电磁场边界条件 电场切向边界条件 考虑麦克斯韦方程组推广的法拉第电磁感应定律 积分回路上的积分结果 面积分结果 lexu@mail.xidian.edu.cn 切向边界条件 11 L S B E dl ds t ∂ ⋅ =− ⋅ ∂ ∫ ∫ 1 2 21 2 1 2 1 ˆˆˆ () ( ) ˆˆ ˆˆ ( ) ( ) l E dl E l l l E l l E E l b n E E l bn E E l ⋅ = ⋅−∆ ∆+ ⋅ = ⋅ − ∆ = × ⋅ − ∆= ⋅ × − ∆ ∫ 0 ˆ lim 0 S h B B ds bh l t t → ∂ ∂ ⋅ = ⋅ ∆= ∂ ∂ ∫ 2 1 nE E ˆ ×−= ( )0 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN