新疆大学：《计量地理学》课程教学实验指导书（负责人：瓦哈甫·哈力克）

ANOVA Sum of Model Squares df Mean Square F Sig. Regression 1754.275 2 877.137 12.861 .001 Residual 818.415 68.201 Total 2572.689 14 a.Predictors:(Constant),Y,X b.Dependent Variable:Z Coefficient Unstandardized Standardized ents Coefficients Model B Std.Error Beta t Sig. 1 (Constant)204.93332.411 6.323 .000 -1.316 ,262 .827 -5.028 .000 -.548 ,397 -.227-1.379 ,193 a.Dependent Variable:Z 经过检验，得到回归系数，根据系数列出回归方程。B分别为常数项，和X、Y的系数

ANOVAb 1754.275 2 877.137 12.861 .001a 818.415 12 68.201 2572.689 14 Regression Residual Total Model 1 Sum of Squares df Mean Square F Sig. a. Predictors: (Constant), Y, X b. Dependent Variable: Z Coefficientsa 204.933 32.411 6.323 .000 -1.316 .262 -.827 -5.028 .000 -.548 .397 -.227 -1.379 .193 (Constant) X Y Model 1 B Std. Error Unstandardized Coefficients Beta Standardized Coefficients t Sig. a. Dependent Variable: Z 经过检验，得到回归系数，根据系数列出回归方程。B 分别为常数项，和 X、Y 的系数。 17

试验4时间序列分析 41[实验目的] 用SPSS统计软件学会建立时间序列新变量方法 4.2[实验步骤] 4.2.1时间分析的定义： 时间序列，也叫时间数列或动态数列，是要素（变量）的数据按照时间顺序变动列而 形成的一种数列，它反映了要素（变量）随时间变化的发展过程。地理过程的时间序列分析， 就是通过分析地理要素（变量）随时间变化的历史过程，揭示其发展变化规律，并对其未来 状态进行预测。 4.2.2时间序列分析中自回归分析实例 在描述实际中出现的某些问题时 一种非常有用的随机模型就是自回归模型 (Autoregression)在该模型中，过程的当前值被表示过程的有穷线性组合在加上一个重击 C我们用XXX2.,记在等间隔时间tt1,t-2,.上的过程值。此外，用Z乙Z,记关 于均值u的偏差，即Z=X-u。则： Z=p乙pZ2t+中pt， 便叫做为P阶自回归(AR)过程，当P=时，称为一阶自回归模型 4.,2.3自回归分析过程 1)定义变量，建立数据文件并输入数据，至少要有一个变量。打开Data菜单中的Define Dates对话框，定义时间序列的周期。采用Transform莱单中的Create Time Series的 方法，建立一个时间序列的新的变量 2)按Analyze→Time series→Autoregression顺序展开相应的对话框。 3)选择一个因变量，将其移到Dependent框。选择一个或多个自变量移到independent(s) 框。在Meda栏中，从三种方法中选择一种预测方法。如果在回归方程中不需要包括 常数项，可不选Include constant in model复选项。 4)单击Save按钮展开保存对话框，在对话框中选择计算结果存放方式。 ●在Create Variables栏中给出 Add to file选项，将新建变量存放在原数据文件中，是系统默认的。 Replace existing选项，用新建变量数据替代数据文件中原先存在的计算结果 Donot create选项，在原数据文件中不建立新变量。 ·%Confidence Interval框，设定置信区间。可在90,95和99三个值中选择其 一，系统默认值是95

试验 4 时间序列分析 4.1 [实验目的] 用 SPSS 统计软件学会建立时间序列新变量方法 4.2 [实验步骤] 4.2.1 时间分析的定义： 时间序列，也叫时间数列或动态数列，是要素（变量）的数据按照时间顺序变动排列而 形成的一种数列，它反映了要素（变量）随时间变化的发展过程。地理过程的时间序列分析， 就是通过分析地理要素（变量）随时间变化的历史过程，揭示其发展变化规律，并对其未来 状态进行预测。 4.2.2 时间序列分析中自回归分析实例 在描述实际中出现的某些问题时，一种非常有用的随机模型就是自回归模型 （Autoregression）.在该模型中，过程的当前值被表示过程的有穷线性组合在加上一个重击 et.我们用Xt,Xt-1,Xt-2,.，记在等间隔时间t,t-1,t-2,.上的过程值。此外，用Zt,Zt-1,Zt-2,.,记关 于均值u的偏差，即Zt=Xt-u。则： Zt=φ 1Zt-1+φ 2Zt-2+.+φ pZt-p+et 便叫做为P阶自回归（AR）过程，当P=1时，称为一阶自回归模型。 4.2.3 自回归分析过程 1) 定义变量，建立数据文件并输入数据，至少要有一个变量。打开 Data 菜单中的 Define Dates 对话框，定义时间序列的周期。采用 Transform 菜单中的 Create Time Series 的 方法，建立一个时间序列的新的变量。 2) 按 Analyze ⇒ Time series ⇒ Autoregression 顺序展开相应的对话框。 3) 选择一个因变量，将其移到 Dependent 框。选择一个或多个自变量移到 independent(s) 框。在 Media 栏中，从三种方法中选择一种预测方法。如果在回归方程中不需要包括 常数项，可不选 Include constant in model 复选项。 4） 单击 Save 按钮展开保存对话框，在对话框中选择计算结果存放方式。 z 在 Create Variables 栏中给出 Add to file 选项，将新建变量存放在原数据文件中，是系统默认的。 Replace existing 选项，用新建变量数据替代数据文件中原先存在的计算结果。 Do not create 选项，在原数据文件中不建立新变量。 z % Confidence Interval 框，设定置信区间。可在 90，95 和 99 三个值中 选择其 一，系统默认值是 95. 18

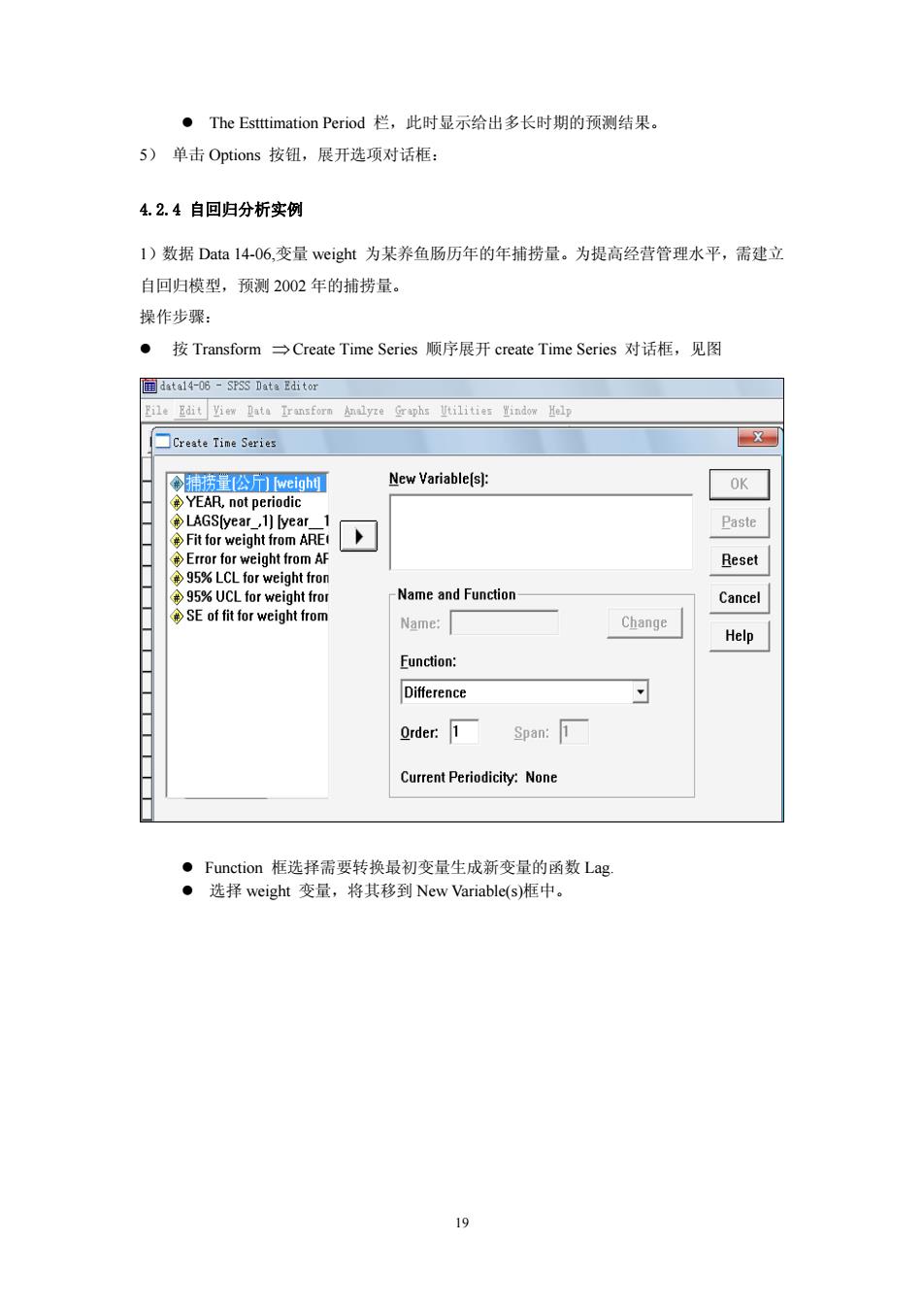
·The Esttimation Period栏，此时显示给出多长时期的预测结果。 5)单击Options按钮，展开选项对话框： 42.4自回归分析实例 1)数据Daa14-06,变量w心ight为某养鱼肠历年的年捕捞量。为提高经营管理水平，需建立 自回归模型，预测2002年的捕捞量。 操作步骤： 。按Transform→Create Time Series顺序展开create Time Series对话框，见图 File Edit View Data Transforn Analyze Graphs Vtilities Window Help □Create Tine Series New Variable(s): OK Paste abt from ap Beset 5%LCL for weight fro -Name and Function Cancel Name: Change Help Eunction: Difference Order:1 Span:1 Current Periodicity:None ·Function框选择需要转换最初变量生成新变最的函数Lag ·选择weight变量，将其移到New Variable(s)框中

z The Estttimation Period 栏，此时显示给出多长时期的预测结果。 5） 单击 Options 按钮，展开选项对话框： 4.2.4 自回归分析实例 1）数据 Data 14-06,变量 weight 为某养鱼肠历年的年捕捞量。为提高经营管理水平，需建立 自回归模型，预测 2002 年的捕捞量。 操作步骤： z 按 Transform ⇒Create Time Series 顺序展开 create Time Series 对话框，见图 z Function 框选择需要转换最初变量生成新变量的函数 Lag. z 选择 weight 变量，将其移到 New Variable(s)框中。 19

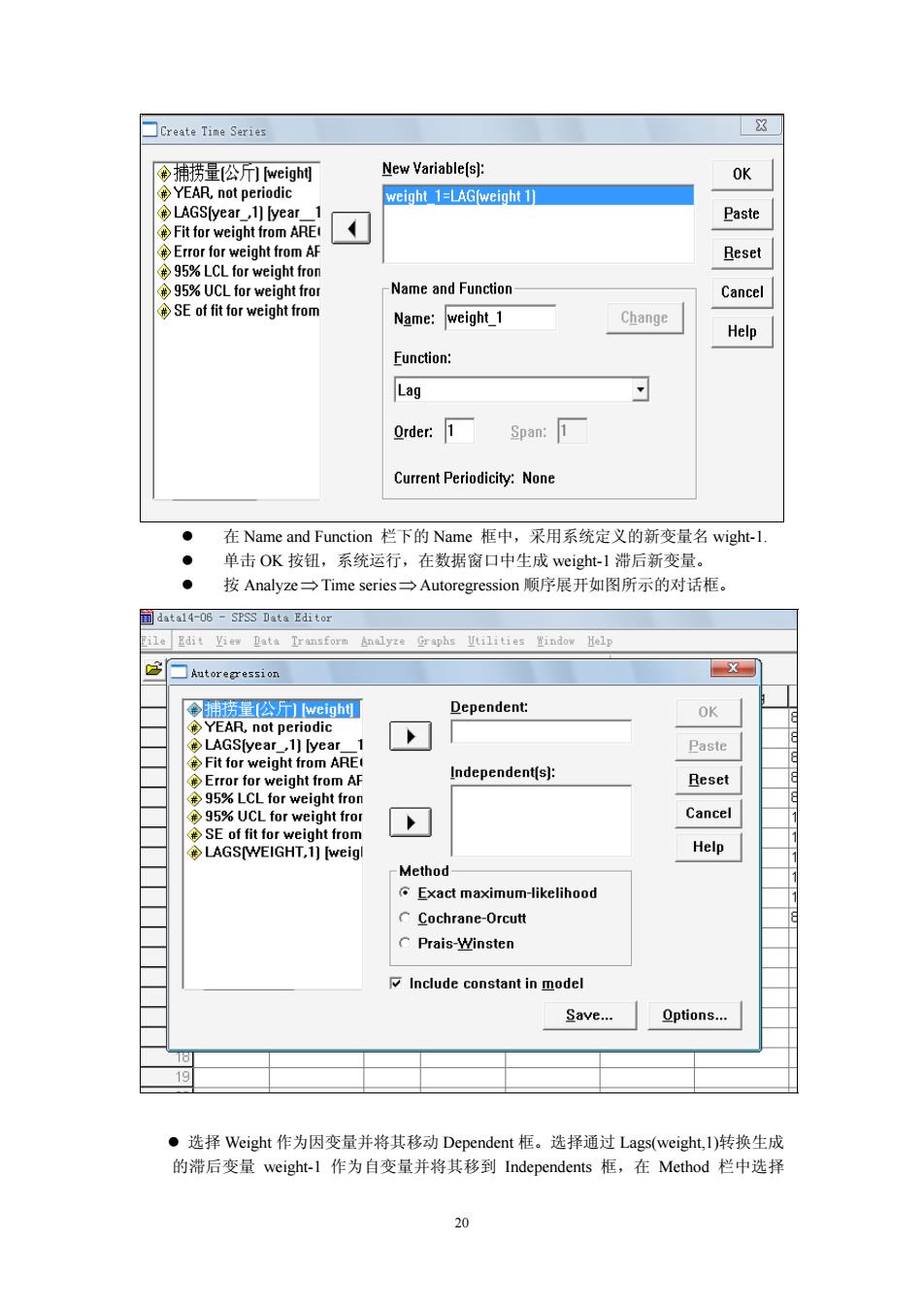
☐Create Tine Series New Variable[s): OK weight 1=LAG/weight 1 ◆LAGS[year,year1 Paste Fit for weight from ARE Reset 95%UCL for weight fror -Name and Function Cancel SE of fit for weight from Name:weight_1 Change Help Function: Lag Order:1 Span:T Current Periodicity:None ● 在Name and Function栏下的Name框中，采用系统定义的新变量名wight-l. 单击OK按钮，系统运行， 在数据窗口中生成 weight-1滞后新变量。 按Analyze→Time series:一Autoregression顺序展开如图所示的对话框 ata4-06-SPSS Dat ito Ie Edit Yiew Data Transform x□ Dependent: OK Paste om A Independent(s]: Reset Cancel 多SE of fit for LAGS(WEIGHT.1]weigl Help Exact maximum-likelihood CCochrane-Orcutt C Prais-Winsten Include constant in model Save.Options. ●选择Weight作为因变量并将其移动Dependent框。选择通过Lags(weight,.I)转换生成 的滞后变量weight-.l作为自变量并将其移到Independents框，在Method栏中选择

z 在 Name and Function 栏下的 Name 框中，采用系统定义的新变量名 wight-1. z 单击 OK 按钮，系统运行，在数据窗口中生成 weight-1 滞后新变量。 z 按 Analyze⇒Time series⇒Autoregression 顺序展开如图所示的对话框。 z 选择 Weight 作为因变量并将其移动 Dependent 框。选择通过 Lags(weight,1)转换生成 的滞后变量 weight-1 作为自变量并将其移到 Independents 框，在 Method 栏中选择 20

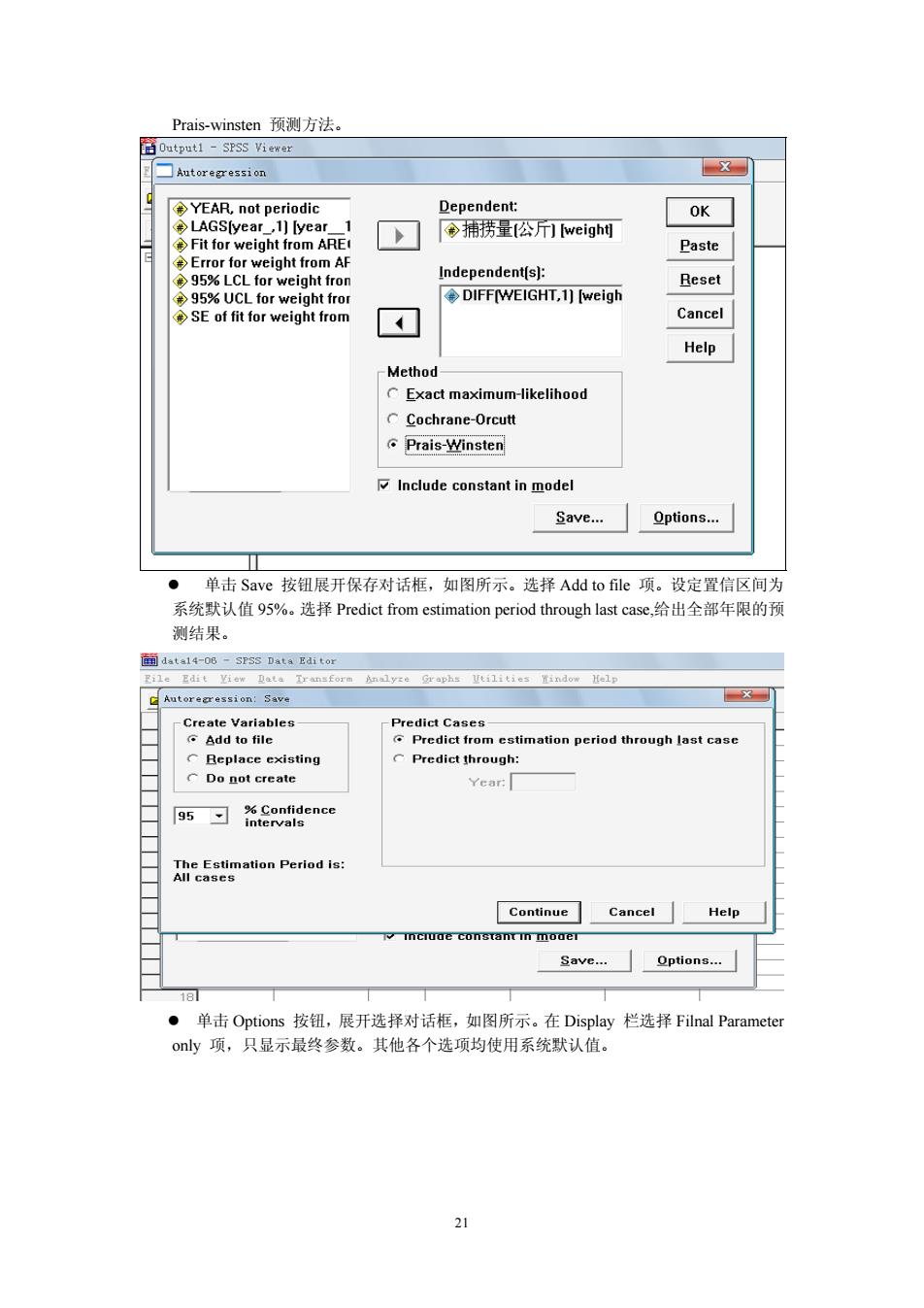
Prais.insten预测方法 眉0 utput1-SPSs1eWer Autoregression X not per Dependent OK Fit for 捕携量公T weight weight from ARE Paste 95%LCL w Reset ◆DIFF(WEIGHT,1)weigh Cancel Help Method Exact maximum-likelihood Cochrane-Orcut Prais-Winsten Include constant in model Save. Options. 单击Save按钮展开保存对话框，如图所示。选择Add to file项。设定置信区间为 系统默认值9S%。选择Predict from estimation period through last case,.给出全部年限的预 测结果。 Edit View 卫at,Iransfors anslyr+raphs Iti1ti道indow Felp Create Variables Predict Cases ation period through last c existing Predict through: C Do not create Continue☐Cancel Help ●单击Options按钮，展开选择对话框，如图所示。在Display栏选择Filnal Parameter oly项，只显示最终参数。其他各个选项均使用系统默认值。 21

Prais-winsten 预测方法。 z 单击 Save 按钮展开保存对话框，如图所示。选择 Add to file 项。设定置信区间为 系统默认值 95%。选择 Predict from estimation period through last case,给出全部年限的预 测结果。 z 单击 Options 按钮，展开选择对话框，如图所示。在 Display 栏选择 Filnal Parameter only 项，只显示最终参数。其他各个选项均使用系统默认值。 21