
两例的共同點 ■有两個參與者,A和B。 ■每個參與者都有兩個策略,C和D ■共有四個策略組合: (C,C),(C,D),D,C),D,D)。 雙方都知道各策略組合的得失
兩例的共同點 有兩個參與者,A 和 B 。 每個參與者都有兩個策略 ,C 和D 。 共有四個策略組合 : (C, C) , (C, D) , (D, C), (D, D) 。 雙方都知道各策略組合的得失
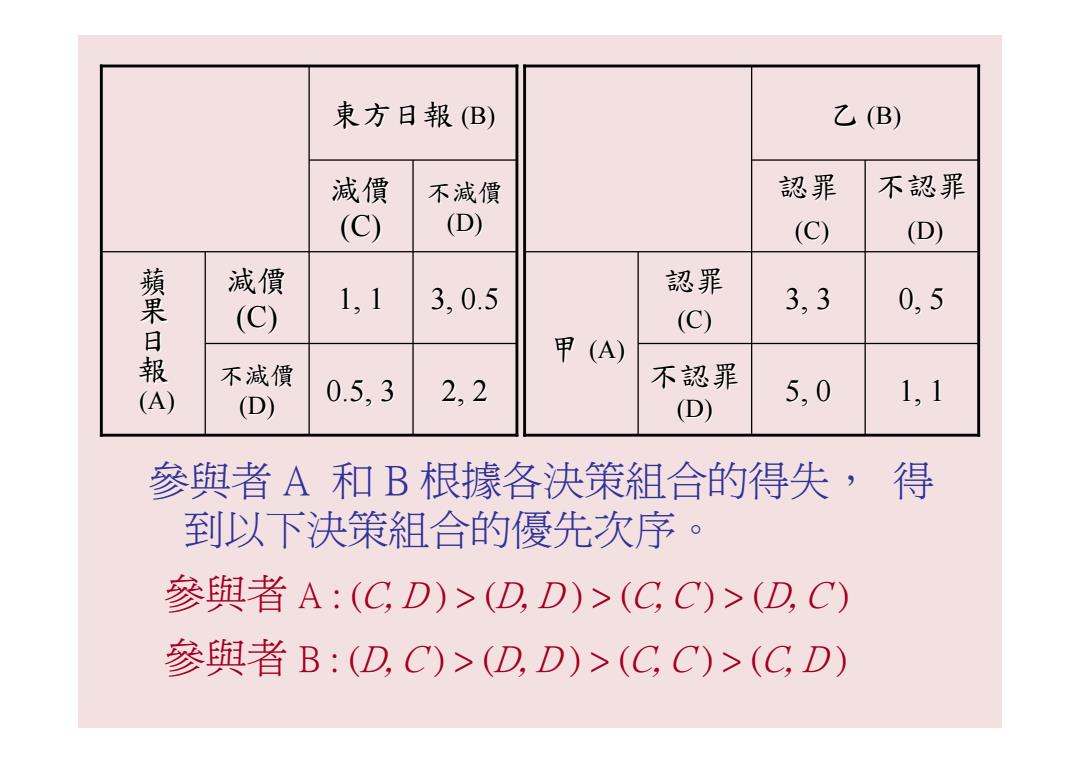
東方日報(B) 乙(B) 減價 不減價 認罪 不認罪 (C) (D) (C) (D) 蘋果 減價 1,1 3,0.5 認罪 (C) 3,3 0,5 (C) 報 甲(A) 不減價 0.5,3 2,2 不認罪 (A) (D) 5,0 (D) 1,1 參與者A和B根據各决策組合的得失,得 到以下决策組合的優先次序。 參與者A:(C,D)>(D,D)>(C,C)>(D,C) 參與者B:(D,C)>(D,D)>(C,C)>(CD)
參與者 A 和 B 根據各決策組合的得失, 得 到以下決策組合的優先次序。 不 5, 0 1, 1 不認罪 (D) 3, 3 0, 5 認罪(C) 甲 (A) 不認罪 (D) 認罪 (C) 乙 (B) 0.5, 3 2, 2 不減價 (D) 1, 1 3, 0.5 減價 (C) 蘋 果 日 報 (A) 不減價 (D) 減價 (C) 東方日報 (B) 參與者 A : (C, D ) > (D, D ) > (C, C ) > (D, C ) 參與者 B : (D, C ) > (D, D ) > (C, C ) > (C, D )

·參與者A:(C,D)>(D,D)>(C,C)>(D,C) 參與者B:(D,C)>(D,D)>(C,C)>(C,D) ·如果我們能根據以上資料,分析出A和B的 選擇,則可把結果應用到以上兩例。 我們將看到A和B都會選C, 雕然他們都知道(D,D)>(C,C)
y 參與者 A : (C, D ) > (D, D ) > (C, C ) > (D, C ) y 參與者 B : (D, C ) > (D, D ) > (C, C ) > (C, D ) y 如果我們能根據以上資料,分析出 A 和 B 的 選擇,則可把結果應用到以上兩例。 y 我們將看到 A 和 B 都會選C , 雖然他們都知道 (D, D ) > (C, C )

何謂博弈? ■前兩例都是博弈論(Game Theory)裹博弈(game)的例子 ■每個博弈(game)是由以下四個 條件來界定
前兩例都是博弈論 (Game Theory)裏博弈(game) 的例子。 每個博弈(game)是由以下四個 條件來界定。 何謂博弈?

博弈的界定 1.參與者的數目 2.參與者各自可選擇的全部策略 3.所有可能出現的策略組合 4.各參與者在每個策略組合的得 失
1. 參與者的數目。 2. 參與者各自可選擇的全部策略。 3. 所有可能出現的策略組合。 4. 各參與者在每個策略組合的得 失。 博弈的界定