
应用型人才培养模式下,《高等数学》专业需求 调研报告 一、调研概况 (一)调研背景 在准备和酝酿了半年之久,理科教学部最终形成了《大学数学教学改革方案》, 方案中要求先对涉及面最广的《高等数学》进行改革。传统的《高等数学》课程 教学内容系统憂求面面俱到,追求理论上的严谨,而往往忽视了数学应用能力的 培养。这不仅不能适应当今科技快速发展、知识日新月异的时代要求,特别是与 应用技能型人才培养有较大的背离或矛盾。我们认为。《高等数学》课程不但为 后继各课程的学习莫定数学基础,而且更应致力于培养学生分析问题、解决问题 的能力,要有利于高素质技能型人才的培养。 (二)调研目的 为了提高数学教学的针对性,提高专业服务接口功能,同时结合学生的基础, 特在学校开设《高等数学》课程的专业中进行了调研。根据调研结果,对数据进 行分析,确定各专业的上课内容和上课重难点,知强数序数学的针对性。 (三)调研对象 调研对象为江西科技学院所有的本科工科专业和开设了《高等数学》课程的 文科专业。 (四)调研时间 2014年9月-10月 (五)调研方式 理科教学部提供《高等数学教学需求调研表》,各学院以专业为单位,教研 室主任或专业负责人组织专业任课教师讨论填写并签字确认,最后学院教务办主 任审核并签字确认。 二、调研结果及分析 (一)各专业对高等数学需求分类原则及分类结果 通过分析调研数据,按照不同专业的需求,结合课程本身的特点,将《高等 数学》划分成三大类,即 经济管理类:会计、财务管理、市场营销、国际贸易、工商管理、物流、旅游 工程管理、汽车服务、人力资源 工程一类:机板工程、材料科学、机板制造、车辆工程、物联网、计算机科学、 土木工程 工程二类:电信、通信
- 11 - 应用型人才培养模式下,《高等数学》专业需求 调研报告 一、调研概况 (一)调研背景 在准备和酝酿了半年之久,理科教学部最终形成了《大学数学教学改革方案》, 方案中要求先对涉及面最广的《高等数学》进行改革。传统的《高等数学》课程 教学内容系统要求面面俱到,追求理论上的严谨,而往往忽视了数学应用能力的 培养。这不仅不能适应当今科技快速发展、知识日新月异的时代要求,特别是与 应用技能型人才培养有较大的背离或矛盾。我们认为,《高等数学》课程不但为 后继各课程的学习奠定数学基础,而且更应致力于培养学生分析问题、解决问题 的能力,要有利于高素质技能型人才的培养。 (二)调研目的 为了提高数学教学的针对性,提高专业服务接口功能,同时结合学生的基础, 特在学校开设《高等数学》课程的专业中进行了调研。根据调研结果,对数据进 行分析,确定各专业的上课内容和上课重难点,加强数序教学的针对性。 (三)调研对象 调研对象为江西科技学院所有的本科工科专业和开设了《高等数学》课程的 文科专业。 (四)调研时间 2014 年 9 月-10 月 (五)调研方式 理科教学部提供《高等数学教学需求调研表》,各学院以专业为单位,教研 室主任或专业负责人组织专业任课教师讨论填写并签字确认,最后学院教务办主 任审核并签字确认。 二、调研结果及分析 (一)各专业对高等数学需求分类原则及分类结果 通过分析调研数据,按照不同专业的需求,结合课程本身的特点,将《高等 数学》划分成三大类,即 经济管理类:会计、财务管理、市场营销、国际贸易、工商管理、物流、旅游 工程管理、汽车服务、人力资源 工程一类:机械工程、材料科学、机械制造、车辆工程、物联网、计算机科学、 土木工程 工程二类:电信、通信
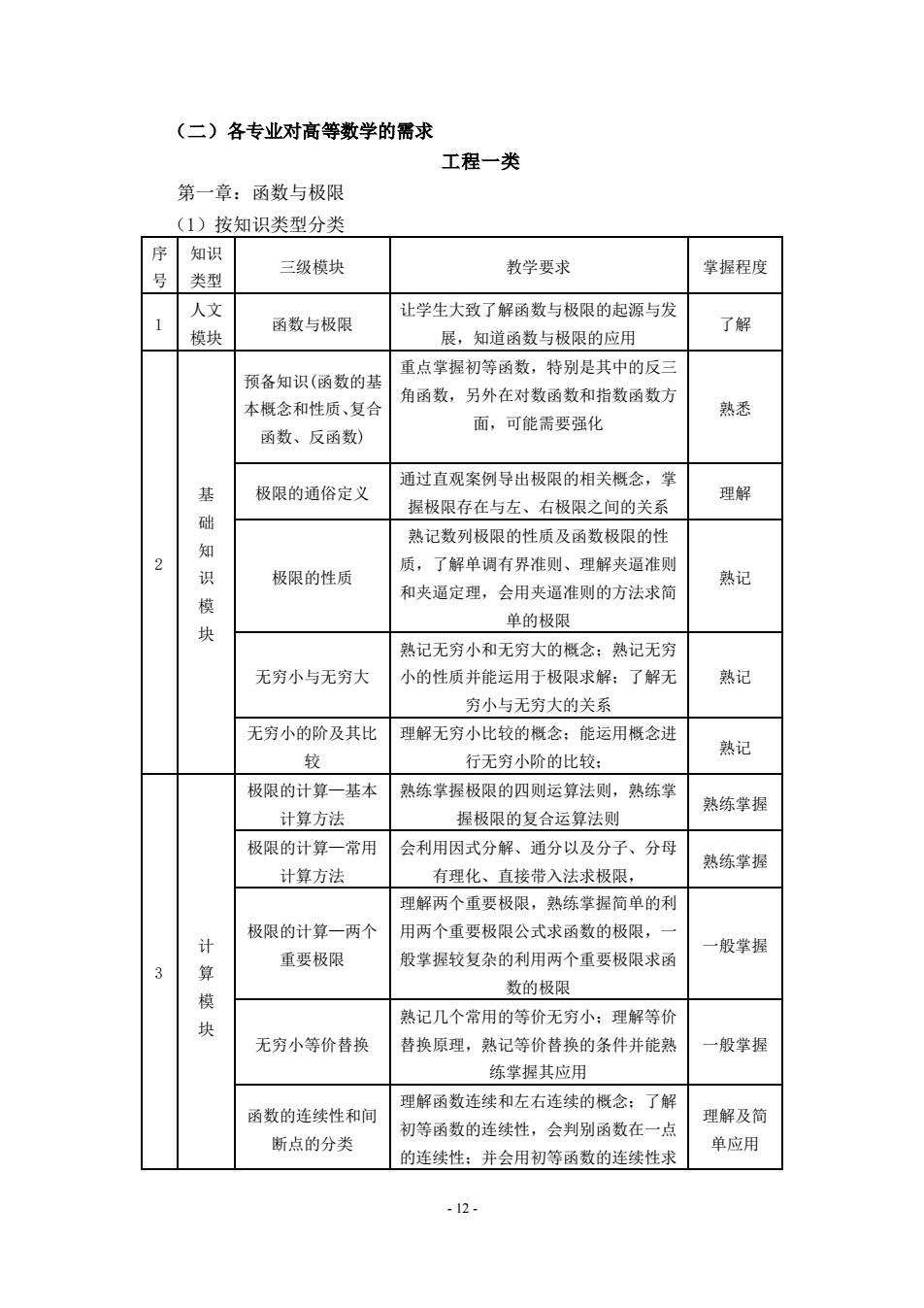
(二)各专业对高等数学的需求 工程一类 第一章:函数与极限 (1)按知识类型分类 序 知识 三级模块 教学要求 拿捉程度 号 类型 人文 让学生大致了解函数与极限的起源与发 函数与极限 了解 核块 展,知道函数与极限的应用 重点掌握初等函数,特别是其中的反三 顶备知识(函数的基 角函数,另外在对数函数和指数函数方 本概念和性质,复合 熟卷 面,可能需要强化 函数、反函数) 通过直观案例导出极限的相关概念,拿 基 极限的通俗定义 理解 握极限存在与左、右极限之间的关系 础 知 熟记数列极限的性质及函数极限的性 2 质,了解单调有界准则,理解夹逼准则 极限的性质 熟记 和夹逼定理,会用夹通准则的方法求简 块 单的极限 然记无穷小和无穷大的概念:熟记无穷 无穷小与无穷大 小的性质并能运用于极限求解:了解无 然记 穷小与无穷大的关系 无穷小的阶及其比 理解无穷小比较的餐名:能运用:名进 较 行无穷小阶的比较: 熟记 极限的计算一基本 然练掌挥极限的四则运算法则,熟练草 熟筑草界 计算方法 捏极限的复合运算法测 极限的计算一常用 会利用因式分解、通分以及分子、分母 熟练草界 计算方法 有理化、直接带入法求极限。 理解两个重要极限。熟练家握简单的利 极限的计算一两个 用两个重要极限公式求函数的极限,一 计 一般草据 重要极限 般拿据较复条的利用两个重要极限求函 3 算 数的极限 块 然记几个常用的等价无穷小:理解等价 无穷小等价骨换 督换原理,熟记等价替换的条件并能熟 般草星 练拿握其应用 理解函数连续和左右连续的概之:了解 函数的连续性和间 理解及简 初等函数的连续性,会判别函数在一点 断点的分类 的连续性:并会用初等橘数的连续性求 单应用 -2-
- 12 - (二)各专业对高等数学的需求 工程一类 第一章:函数与极限 (1)按知识类型分类 序 号 知识 类型 三级模块 教学要求 掌握程度 1 人文 模块 函数与极限 让学生大致了解函数与极限的起源与发 展,知道函数与极限的应用 了解 2 基 础 知 识 模 块 预备知识(函数的基 本概念和性质、复合 函数、反函数) 重点掌握初等函数,特别是其中的反三 角函数,另外在对数函数和指数函数方 面,可能需要强化 熟悉 极限的通俗定义 通过直观案例导出极限的相关概念,掌 握极限存在与左、右极限之间的关系 理解 极限的性质 熟记数列极限的性质及函数极限的性 质,了解单调有界准则、理解夹逼准则 和夹逼定理,会用夹逼准则的方法求简 单的极限 熟记 无穷小与无穷大 熟记无穷小和无穷大的概念;熟记无穷 小的性质并能运用于极限求解;了解无 穷小与无穷大的关系 熟记 无穷小的阶及其比 较 理解无穷小比较的概念;能运用概念进 行无穷小阶的比较; 熟记 3 计 算 模 块 极限的计算—基本 计算方法 熟练掌握极限的四则运算法则,熟练掌 握极限的复合运算法则 熟练掌握 极限的计算—常用 计算方法 会利用因式分解、通分以及分子、分母 有理化、直接带入法求极限, 熟练掌握 极限的计算—两个 重要极限 理解两个重要极限,熟练掌握简单的利 用两个重要极限公式求函数的极限,一 般掌握较复杂的利用两个重要极限求函 数的极限 一般掌握 无穷小等价替换 熟记几个常用的等价无穷小;理解等价 替换原理,熟记等价替换的条件并能熟 练掌握其应用 一般掌握 函数的连续性和间 断点的分类 理解函数连续和左右连续的概念;了解 初等函数的连续性,会判别函数在一点 的连续性;并会用初等函数的连续性求 理解及简 单应用

简单的极限。了解函数间斯点的定义, 掌摆间断点的分类及特征:掌握间断点 的判别方法 闭区间上连线函数 了解闭区间上连铁函数的性质:重点常 的性质 理解 探零点存在定理的应用 极限的应用之渐近 了解建模步露,理解渐近线的建模过程: 器艺渐近线的类别及其特狂,拿据渐近 简单应用 线 线的求解 函数的应用之二分 了解二分法:会用二分法求解方程的近 法 似解 了解 (2)按服务对象分类 服务 三级模块 知识类型 地位、作用 号 对象 预备知识 基础模块 高等数学如识的基础 通过人文概述,让学生能系统地了 人文概述(概括人文模块) 基础模块 解模块内容要学什么、为什么要 学、怎么去学 极限的通俗定义 基础械块 极限部分的理论基础 极限的性质 基础模块 极限部分的理论基础 极限计算的基础,两个重要极限公 无穷小与无穷大 基础模块 式的基础 无穷小的阶及其比较 基础模块 无穷小等价替换的基础 1 极限的计算一基本计算方 计算模块 极限计算的基础 法 识 极限的计算一常用计算方 计算模块 模 法 较复杂的函数计算的基础 极限的计算一两个重要极 计算械块 用于专业中较复杂的极限计算 限 无穷小等价替换 计算核块 用于专业中较复杂的极限计算 函数的连续性和间断点的 应用板块 问断点分类的基础 分类 用区间上走续函数的性质 应用模块 二分法的基础 专业 极限的应用之新近线 应用模块 2 服务 模块 函数的应用之二分法 位用械块 个 单调有界准测、夹通准则 3 计算模块 深度掌握,为考研服务 性 和夹通定理 -13-
- 13 - 简单的极限。了解函数间断点的定义; 掌握间断点的分类及特征;掌握间断点 的判别方法 闭区间上连续函数 的性质 了解闭区间上连续函数的性质;重点掌 握零点存在定理的应用 理解 极限的应用之渐近 线 了解建模步骤,理解渐近线的建模过程; 熟悉渐近线的类别及其特征,掌握渐近 线的求解 简单应用 函数的应用之二分 法 了解二分法;会用二分法求解方程的近 似解 了解 (2)按服务对象分类 序 号 服务 对象 三级模块 知识类型 地位、作用 1 通 识 模 块 预备知识 基础模块 高等数学知识的基础 人文概述(概括人文模块) 基础模块 通过人文概述,让学生能系统地了 解模块内容要学什么、为什么要 学、怎么去学 极限的通俗定义 基础模块 极限部分的理论基础 极限的性质 基础模块 极限部分的理论基础 无穷小与无穷大 基础模块 极限计算的基础、两个重要极限公 式的基础 无穷小的阶及其比较 基础模块 无穷小等价替换的基础 极限的计算—基本计算方 法 计算模块 极限计算的基础 极限的计算—常用计算方 法 计算模块 较复杂的函数计算的基础 极限的计算—两个重要极 限 计算模块 用于专业中较复杂的极限计算 无穷小等价替换 计算模块 用于专业中较复杂的极限计算 函数的连续性和间断点的 分类 应用模块 间断点分类的基础 闭区间上连续函数的性质 应用模块 二分法的基础 2 专业 服务 模块 极限的应用之渐近线 应用模块 函数的应用之二分法 应用模块 3 个 性 单调有界准则、夹逼准则 和夹逼定理 计算模块 深度掌握,为考研服务
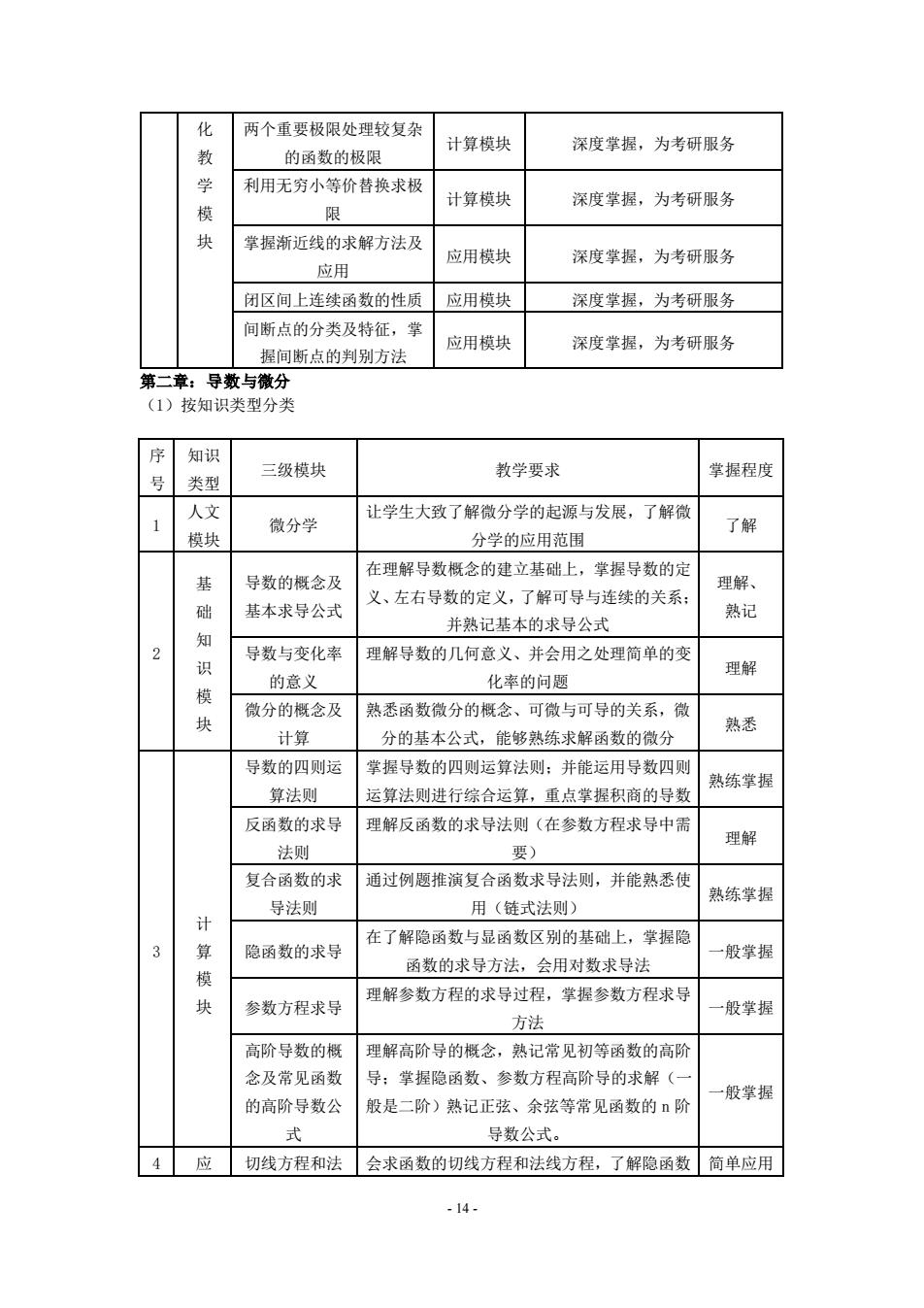
化 两个重要极限处理较复杂 计算模块 深度掌握,为考研服务 的函数的极限 学 利用无穷小等价替换求极 计算根块 深度掌握,为考研服务 模 限 块 拿握渐近线的求解方法及 应用模块 深度掌握,为考研服务 应用 闭区间上连续橘数的性质 应用模块 深度掌据,为考研服务 间断点的分类及特征,掌 应用模块 深度掌握,为考研服务 握间断点的判别方法 第二章:导数与微分 (1)按知识类型分类 序 知识 三级模块 拿握程度 号 类型 教学要求 人文 让学生大政了解微分学的起源与发展,了解微 微分学 了解 榄块 分学的应用范围 基 在理解导数概念的建立基础上,掌握导数的定 导数的概念及 理解、 义,左右导数的定义,了解可导与连续的关系: 础 基本求导公式 熟记 并熟记基本的求导公式 知 2 导数与变化率 识 理解导数的几何意义、并会用之处理简单的变 理解 模 的意义 化率的思 微分的概念及 熟悉橘数微分的概念、可微与可导的关系,微 计算 分的基本公式。能够熟炼求解函数的微分 熟老 导数的四则运 掌提导数的四则运算法则:并能运用导数四则 熟依草据 算法则 运算法则进行综合运算,重点掌握积商的导数 反雨数的求导 理解反函数的求导法则(在参数方程求导中需 理解 法则 要) 复合函数的求 通过例思推演复合函数求导法则,并能熟悉使 熟练草据 导法则 用(链式法则) 计 算 在了解隐函数与显函数区别的基础上,掌挥隐 隐两数的求导 般拿据 模 函数的求导方法,会用对数求导法 理解参数方程的求导过程,拿据参数方程求导 参数方程求导 般草据 方法 高阶导数的展 理解高阶导的概么,然记常见初等函数的高阶 念及常见函数 导:算捉隐函数、参数方程高阶导的求解(一 一般草据 的高阶导数公 般是二阶)然记正弦、余弦等常见函数的阶 式 导数公式 应 切线方程和法会求函数的切线方程和法线方程,了解隐函数简单应用
- 14 - 化 教 学 模 块 两个重要极限处理较复杂 的函数的极限 计算模块 深度掌握,为考研服务 利用无穷小等价替换求极 限 计算模块 深度掌握,为考研服务 掌握渐近线的求解方法及 应用 应用模块 深度掌握,为考研服务 闭区间上连续函数的性质 应用模块 深度掌握,为考研服务 间断点的分类及特征,掌 握间断点的判别方法 应用模块 深度掌握,为考研服务 第二章:导数与微分 (1)按知识类型分类 序 号 知识 类型 三级模块 教学要求 掌握程度 1 人文 模块 微分学 让学生大致了解微分学的起源与发展,了解微 分学的应用范围 了解 2 基 础 知 识 模 块 导数的概念及 基本求导公式 在理解导数概念的建立基础上,掌握导数的定 义、左右导数的定义,了解可导与连续的关系; 并熟记基本的求导公式 理解、 熟记 导数与变化率 的意义 理解导数的几何意义、并会用之处理简单的变 化率的问题 理解 微分的概念及 计算 熟悉函数微分的概念、可微与可导的关系,微 分的基本公式,能够熟练求解函数的微分 熟悉 3 计 算 模 块 导数的四则运 算法则 掌握导数的四则运算法则;并能运用导数四则 运算法则进行综合运算,重点掌握积商的导数 熟练掌握 反函数的求导 法则 理解反函数的求导法则(在参数方程求导中需 要) 理解 复合函数的求 导法则 通过例题推演复合函数求导法则,并能熟悉使 用(链式法则) 熟练掌握 隐函数的求导 在了解隐函数与显函数区别的基础上,掌握隐 函数的求导方法,会用对数求导法 一般掌握 参数方程求导 理解参数方程的求导过程,掌握参数方程求导 方法 一般掌握 高阶导数的概 念及常见函数 的高阶导数公 式 理解高阶导的概念,熟记常见初等函数的高阶 导;掌握隐函数、参数方程高阶导的求解(一 般是二阶)熟记正弦、余弦等常见函数的 n 阶 导数公式。 一般掌握 4 应 切线方程和法 会求函数的切线方程和法线方程,了解隐函数 简单应用
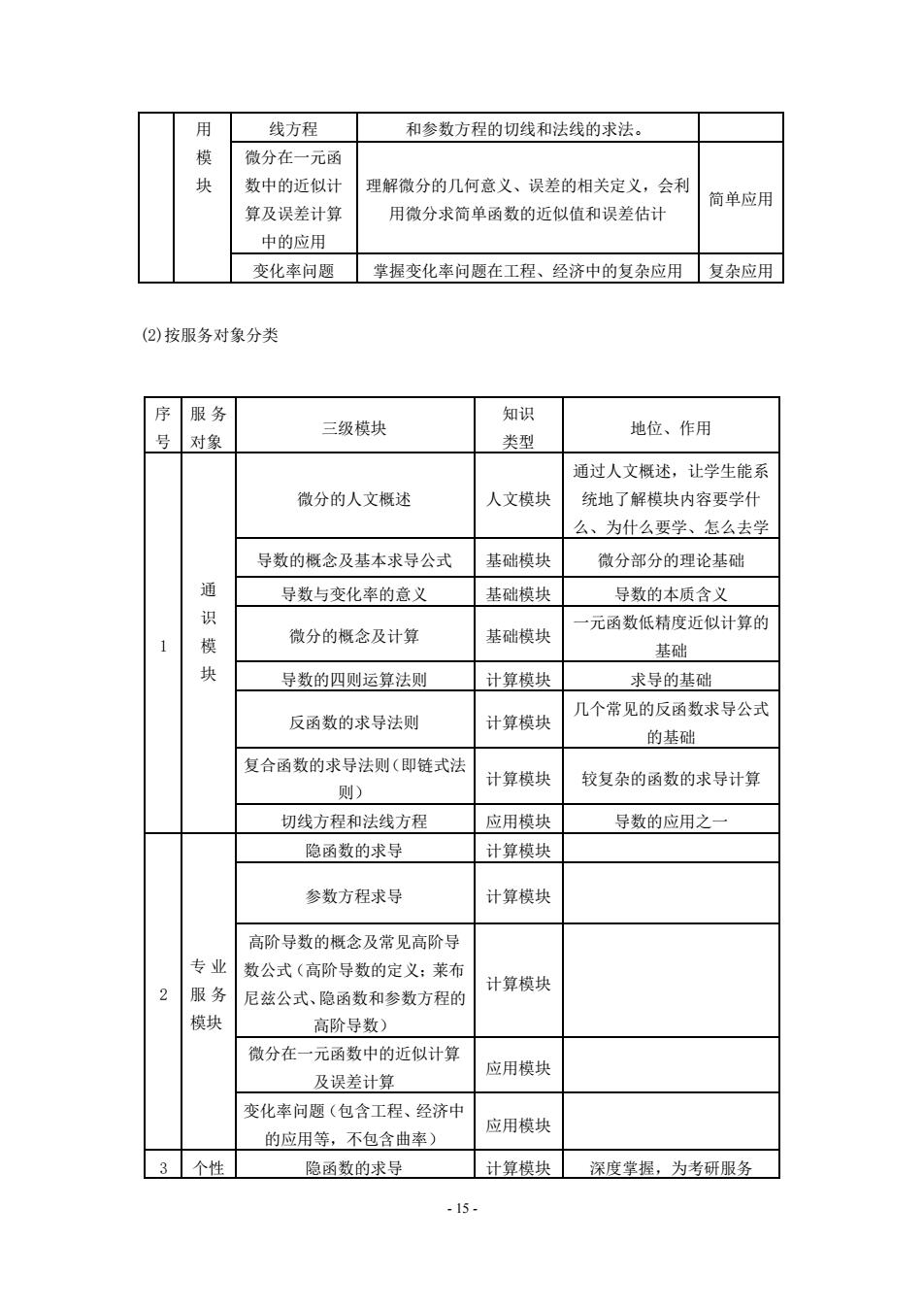
用 线方程 和参量方程的切线和法线的求法。 微分在一元函 块 数中的近似计 理解微分的几何意义、误差的相关定文,会利 简单应用 算及误差计算 用微分求简单函数的道似值和误差估计 中的应用 变化率月题 拿据变化率问题在工程、经济中的复杂应用 复杂应用 (2)按服务对象分类 序 服务 知识 号 对象 三级棱块 类型 地位、作用 通过人文概述,让学生能系 微分的人文概速 人文械块 饶地了解核块内容要学什 么、为什么要学、怎么去学 导数的概念及基本求导公式 暴础模块 微分部分的理论基留 通 导数与变化半的意义 基础模块 导数的本质含义 识 元函数低精度近似计算的 1 被 微分的概老及计算 基础模块 基础 块 导数的四则运算法则 计算模块 求导的基础 几个常见的反函数求导公式 反函数的求导法则 计算模块 的基础 复合函数的求导法则(即链式法 计算模块 较复条的函数的求导计算 则) 切线方程和法线方程 应用模块 导量的应用之一 隐函数的求导 计算模块 参数方程求导 计算模块 高阶导数的概之及常见高阶导 专业 数公式(高阶导数的定义:莱布 服务 计算械块 尼线公式、隐函数和参数方程的 楨块 高阶导数) 微分在一元函数中的近似计算 应用模块 及误差计算 变化率问题(包含工程,经济中 应用根块 的应用等,不包含曲率) 3 个性 隐函数的求导 计算板块 深度掌捏,为考研服务 -15
- 15 - (2)按服务对象分类 用 模 块 线方程 和参数方程的切线和法线的求法。 微分在一元函 数中的近似计 算及误差计算 中的应用 理解微分的几何意义、误差的相关定义,会利 用微分求简单函数的近似值和误差估计 简单应用 变化率问题 掌握变化率问题在工程、经济中的复杂应用 复杂应用 序 号 服 务 对象 三级模块 知识 类型 地位、作用 1 通 识 模 块 微分的人文概述 人文模块 通过人文概述,让学生能系 统地了解模块内容要学什 么、为什么要学、怎么去学 导数的概念及基本求导公式 基础模块 微分部分的理论基础 导数与变化率的意义 基础模块 导数的本质含义 微分的概念及计算 基础模块 一元函数低精度近似计算的 基础 导数的四则运算法则 计算模块 求导的基础 反函数的求导法则 计算模块 几个常见的反函数求导公式 的基础 复合函数的求导法则(即链式法 则) 计算模块 较复杂的函数的求导计算 切线方程和法线方程 应用模块 导数的应用之一 2 专 业 服 务 模块 隐函数的求导 计算模块 参数方程求导 计算模块 高阶导数的概念及常见高阶导 数公式(高阶导数的定义;莱布 尼兹公式、隐函数和参数方程的 高阶导数) 计算模块 微分在一元函数中的近似计算 及误差计算 应用模块 变化率问题(包含工程、经济中 的应用等,不包含曲率) 应用模块 3 个性 隐函数的求导 计算模块 深度掌握,为考研服务