
化教 参数方程求导 计算械块 深度掌握,为考研服务 学模 高阶导最的辰多及常见高阶导 块 数公式(高阶导数的定义:莱布 计算模块 深度掌探,为考研服务 尼盐公式,隐函数和参数方程的 高阶导数) 第三章徽分中值定理及应用 (1)按知识类型分类 序 知识 号 拿无程度 类型 三领模块 教学要求 理解微分中值定理并了解其地位,作用:能用 熟记、一 微分中值定理 基础 微分中值定理解决简单的相关日题 般掌报 知识 在理解秦勒定理的基健上,熟记常见的几种函 模块 熟悉、熟 泰制公式 数的麦克劳林履开式,了解秦勒公式在计算极 记 限、求导、证明方面的应用 函数的单调性 拿据用求导的方法来判断函数的单调性,并会 求函数的极值。会利用函数单调性证明不等 复杂应用 与板值 式。 掌累用洛必塔法则求简单的或四的极限, 00 洛必达法则 知道如何把0,0一,1”,0型转化成 简单应用 应 9或巴求楼限, 00 2 用 草握运用导数求最值的方法,进一步了解建柄 模 函数的优化 简单应用 的基本步霖,理解优化模型一易拉罐的设计 块 雨数的凹凸性 在理解函数凹凸性和拐点的概念的基础上,章 简单应用 与拐点 罪简单函数回凸性的判别方法以及锡点的法 函数的作图 拿无函数的作图过程 复杂应用 理解曲率的概念。 自率及其应用 会求曲线的曲率、由率半径、由率圆,了解曲 简单应用 率的一线简单应用 牛顿选代法 理解牛顿选代公式并能简单应用 简单应用 (3)按服务对象分类 序 服务 知识 三缓核块 号 地位、作用 对象 类型 微分中值定理 基瑙横块 洛必塔法则,泰勒公式的基础 -16-
- 16 - 第三章 微分中值定理及应用 (1)按知识类型分类 序 号 知识 类型 三级模块 教学要求 掌握程度 1 基础 知识 模块 微分中值定理 理解微分中值定理并了解其地位、作用;能用 微分中值定理解决简单的相关问题 熟记、一 般掌握 泰勒公式 在理解泰勒定理的基础上,熟记常见的几种函 数的麦克劳林展开式,了解泰勒公式在计算极 限、求导、证明方面的应用 熟悉、熟 记 2 应 用 模 块 函数的单调性 与极值 掌握用求导的方法来判断函数的单调性,并会 求函数的极值,会利用函数单调性证明不等 式。 复杂应用 洛必达法则 掌握用洛必塔法则求简单的 或 0 0 的极限, 知道如何把 0, − ,1 , 0 ,0 0型 转化成 或 0 0 求极限。 简单应用 函数的优化 掌握运用导数求最值的方法,进一步了解建模 的基本步骤,理解优化模型—易拉罐的设计 简单应用 函数的凹凸性 与拐点 在理解函数凹凸性和拐点的概念的基础上,掌 握简单函数凹凸性的判别方法以及拐点的法 简单应用 函数的作图 掌握函数的作图过程 复杂应用 曲率及其应用 理解曲率的概念, 会求曲线的曲率、曲率半径、曲率圆,了解曲 率的一些简单应用 简单应用 牛顿迭代法 理解牛顿迭代公式并能简单应用 简单应用 (3)按服务对象分类 化教 学模 块 参数方程求导 计算模块 深度掌握,为考研服务 高阶导数的概念及常见高阶导 数公式(高阶导数的定义;莱布 尼兹公式、隐函数和参数方程的 高阶导数) 计算模块 深度掌握,为考研服务 序 号 服务 对象 三级模块 知识 类型 地位、作用 微分中值定理 基础模块 洛必塔法则、泰勒公式的基础
通 提供了一种比较通用和简便 洛必达法则 应用械块 识 的求极限的方法 慎 函数的单调性和极值 应用极块 最值的基础、函数作图的基础 块 函数的图凸性与拐点 应用榄块 函数作图的基础 函数的作图 应用模块 专 泰勒公式 基础模块 用于工程上的高精度计算 业 可以用于解决实际生活中的 函数的优化 应用模块 最植问愿 2 务 机械,汽车,土木专业课程学 曲率及其应用 应用模块 核 习需要 块 方程的近似解 应用核块 微分中植定理的理解、掌握及 基础模块 深度拿据。为考研服务 应用 泰勒公式 基础模块 深度草挥,为考研服务 个 不等式的证明(用凹凸性、单 应用模块 深度草据。为考研服务 性 调性,最值知识) 化 掌握用洛必塔法测求复杂的 3 教 学 Q或的楼限,章握如何把 0 慎 应用极块 深度拿据。为考研服务 06,的-,1“,°,0型转 块 化成或巴求极限。 00 常握曲率的概念,并会求曲率 应用械块 深度章据,为考研服务 第四章一元函数积分学 (1)按知如识类型分类 序号 知讯类型 三级模块 教学要求 掌据程度 积分学“人物概 让学生大致了解积分学的起源与发 1 人文模块 了解 逃” 展,以及积分学的应用 定积分的概念 理解并熟记定积分的概念 热记 基 定积分的几何意 熟悉定积分的几何意义:熟透定积分 础 义和性质 的性质 熟悉 知 2 在理解变上限积分函数与原函数关 识 变上限积分函数 视 系的基础上,掌握变限积分函数的导 一般草显 及其导数 块 数 微积分基本定理 在理解微积分基本定理的基础上,会 熟记 -17-
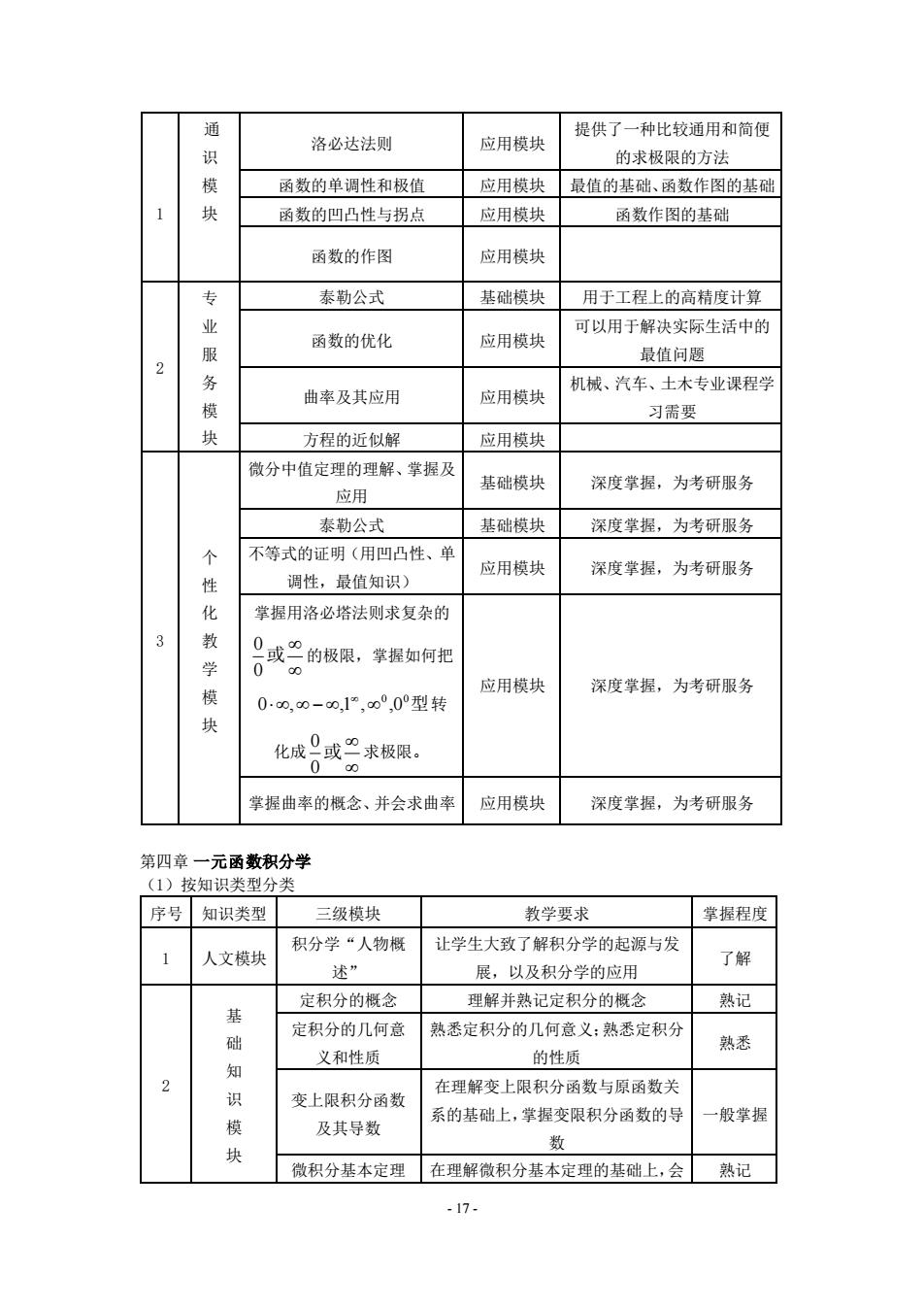
- 17 - 第四章 一元函数积分学 (1)按知识类型分类 序号 知识类型 三级模块 教学要求 掌握程度 1 人文模块 积分学“人物概 述” 让学生大致了解积分学的起源与发 展,以及积分学的应用 了解 2 基 础 知 识 模 块 定积分的概念 理解并熟记定积分的概念 熟记 定积分的几何意 义和性质 熟悉定积分的几何意义;熟悉定积分 的性质 熟悉 变上限积分函数 及其导数 在理解变上限积分函数与原函数关 系的基础上,掌握变限积分函数的导 数 一般掌握 微积分基本定理 在理解微积分基本定理的基础上,会 熟记 1 通 识 模 块 洛必达法则 应用模块 提供了一种比较通用和简便 的求极限的方法 函数的单调性和极值 应用模块 最值的基础、函数作图的基础 函数的凹凸性与拐点 应用模块 函数作图的基础 函数的作图 应用模块 2 专 业 服 务 模 块 泰勒公式 基础模块 用于工程上的高精度计算 函数的优化 应用模块 可以用于解决实际生活中的 最值问题 曲率及其应用 应用模块 机械、汽车、土木专业课程学 习需要 方程的近似解 应用模块 3 个 性 化 教 学 模 块 微分中值定理的理解、掌握及 应用 基础模块 深度掌握,为考研服务 泰勒公式 基础模块 深度掌握,为考研服务 不等式的证明(用凹凸性、单 调性,最值知识) 应用模块 深度掌握,为考研服务 掌握用洛必塔法则求复杂的 或 0 0 的极限,掌握如何把 0, − ,1 , 0 ,0 0型 转 化成 或 0 0 求极限。 应用模块 深度掌握,为考研服务 掌握曲率的概念、并会求曲率 应用模块 深度掌握,为考研服务
用微积分基本定理计算简单的定积 分 不定积分的概念 理解星函数的概念:理解不定积分的 熟记 和基本积分公式 慢念:熟记不定积分的基本积分公式 定积分中的重要 了解利用函数的奇偶性,周期性计算 了解 结论 定机分 停据微元法的原理,热记微元法的主 微元法 热记 要步骤、及使用条件 利用不定积分的 熟悉不定积分的性质并能运用于不 性质计算简单的 熟草显 定积分的计算 不定积分 凑微分法 理解凑微分法的原理并能熟练草据 熟练拿罪 停据不定积分的根式换元法、三角换 第二换元法(一) 熟炼掌握 元法及倒代法求不定积分 拿握定积分的根式换元法,三角换元 第二换元法(二) 熟练草握 法及倒代法求定积分 分部积分法(一) 理解分部积分公式,并然练掌挥求函 熟练草挥 数不定积分: 理解分部积分公式,并熟练掌捏求函 分部积分法(二) 熟练掌挥 数定积分: 计 3 热练掌握三类三角函数的不定积分 算 三角函数的积分 与定积分:了解三角函数积分的特殊 熟陈掌握 板 技巧 典 了解有理函数的定义,熟练掌挥简单 有理函数的积分 有理雨数的积分:紫握有理函数的分 一般掌握 解 可化为有理函数 了解三角有理式的积分:了解某些无 的积分 了解 理根式的积分 了解无穷区间上广义积分的定文和 无穷区间上的广 性质:掌握无穷区间上广义积分的计 一般草握 义积分 算 了解无界函数的广义积分的定义和 无界函数的广义 性质:掌握无界函数的广义积分的计 一般掌握 积分 算 应 含变限积分的极 草强含变限积分的极限的求解 一般掌挥 用 限间愿 被 数值积分及其应 了解数植积分的几种最基本方法: 了解 -18
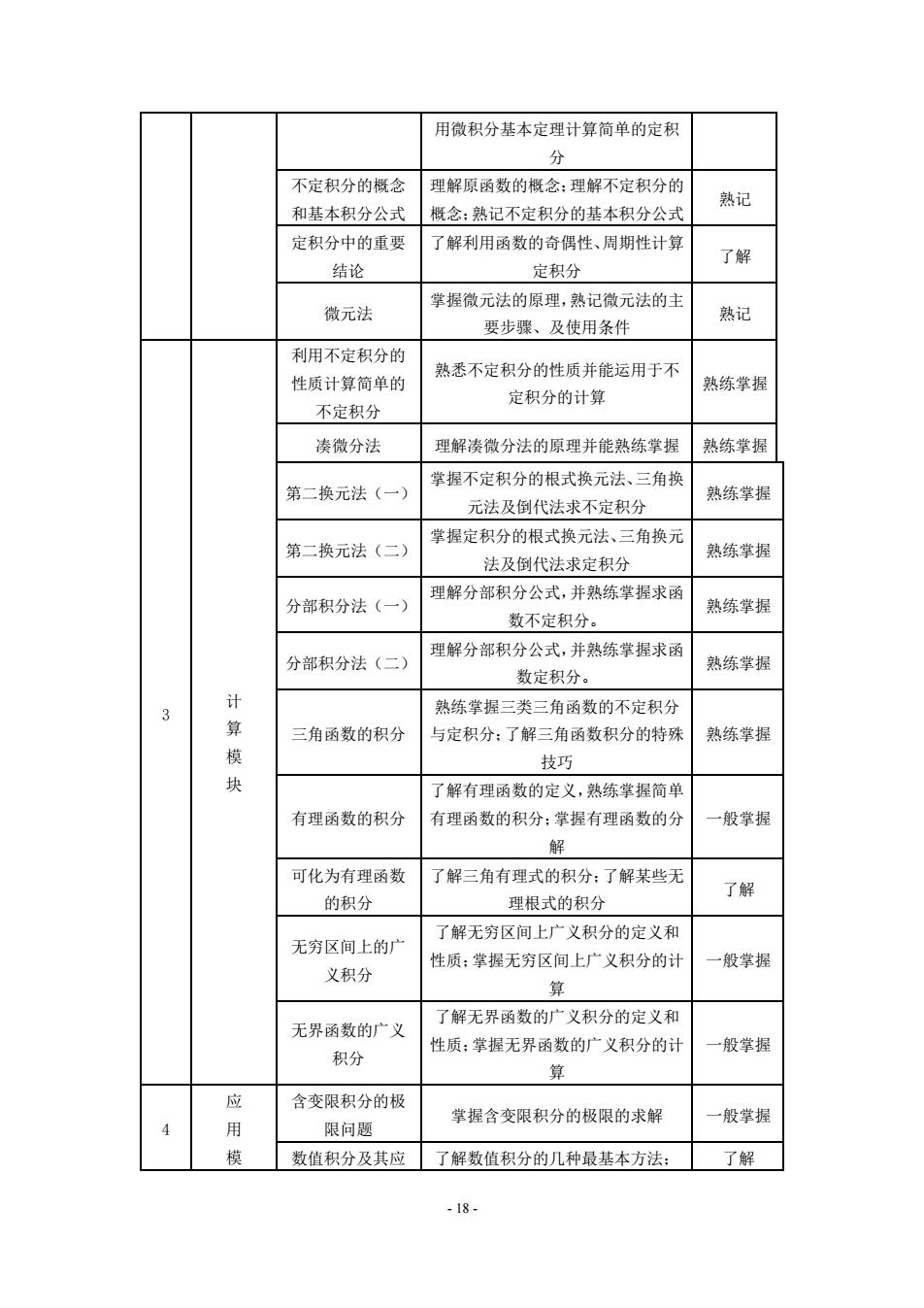
- 18 - 用微积分基本定理计算简单的定积 分 不定积分的概念 和基本积分公式 理解原函数的概念;理解不定积分的 概念;熟记不定积分的基本积分公式 熟记 定积分中的重要 结论 了解利用函数的奇偶性、周期性计算 定积分 了解 微元法 掌握微元法的原理,熟记微元法的主 要步骤、及使用条件 熟记 3 计 算 模 块 利用不定积分的 性质计算简单的 不定积分 熟悉不定积分的性质并能运用于不 定积分的计算 熟练掌握 凑微分法 理解凑微分法的原理并能熟练掌握 熟练掌握 第二换元法(一) 掌握不定积分的根式换元法、三角换 元法及倒代法求不定积分 熟练掌握 第二换元法(二) 掌握定积分的根式换元法、三角换元 法及倒代法求定积分 熟练掌握 分部积分法(一) 理解分部积分公式,并熟练掌握求函 数不定积分。 熟练掌握 分部积分法(二) 理解分部积分公式,并熟练掌握求函 数定积分。 熟练掌握 三角函数的积分 熟练掌握三类三角函数的不定积分 与定积分;了解三角函数积分的特殊 技巧 熟练掌握 有理函数的积分 了解有理函数的定义,熟练掌握简单 有理函数的积分;掌握有理函数的分 解 一般掌握 可化为有理函数 的积分 了解三角有理式的积分;了解某些无 理根式的积分 了解 无穷区间上的广 义积分 了解无穷区间上广义积分的定义和 性质;掌握无穷区间上广义积分的计 算 一般掌握 无界函数的广义 积分 了解无界函数的广义积分的定义和 性质;掌握无界函数的广义积分的计 算 一般掌握 4 应 用 模 含变限积分的极 限问题 掌握含变限积分的极限的求解 一般掌握 数值积分及其应 了解数值积分的几种最基本方法; 了解

块 用 了解数值积分的误差估计 理解微无法在平面图彩面积的应用: 平面图形的面积 拿握直角坐标系下、极坐标系下面积 简单应用 的求解 理解微分法在立体体积的应用,拿塑 运用定积分求简单的旋转体的体积, 立体的体积 简单应用 了解平行徒面面积为己知的立体的 体积 理解平面曲线或长的定义: 曲线的流长 简单应用 掌挥简单无长的求法 定积分的物理应 掌据定积分在物理中的简单应用 简单应用 用 (2)按服务对象分类 序服务 三级模块 知洪类型 地位、作用 号对象 通过人文概述,让学生能系统地了解 人文概述 人文横块 横块内容要学什么、为什么要学、怎 么去学 定积分的概么 基础模块 定积分的理论基罐 定积分的几何意义和性 定积分的理论基础、求平面图形的面 质 基础模块 积的理论基础 变上限积分函数及其导 微积分基本定理的基酪,求带变限函 基础模块 数 数积分极限的基础 通 微积分基本定理 基础核块 定积分计算的理论基础 识 不定积分的顺念和基本 1 核 基础模块 定积分计算的基础 块 积分公式 定积分用于处理实际何思的理论原 微元法 基础模块 理 利用不定积分的性质计 计算模块 用于计算简单的不定积分 算简单的不定凯分 流微分法 计算模块 〔不)定积分的常用计算方法 第二换元法(一)、(二) 计算榄块 (不)定积分的常用计算方法 分部积分法(一)、(二) 计算模块 (不)定积分的常用计算方法 三角函数的积分 计算模块 用于计算有关三角函数的积分 平面图形的面积 应用模块 定积分的几何应用之一 专 定积分中的重要结论 基街模块 有理函数的积分 计算模块 -19-
- 19 - 块 用 了解数值积分的误差估计 平面图形的面积 理解微元法在平面图形面积的应用; 掌握直角坐标系下、极坐标系下面积 的求解 简单应用 立体的体积 理解微分法在立体体积的应用,掌握 运用定积分求简单的旋转体的体积、 了解平行截面面积为已知的立体的 体积 简单应用 曲线的弧长 理解平面曲线弧长的定义; 掌握简单弧长的求法 简单应用 定积分的物理应 用 掌握定积分在物理中的简单应用 简单应用 (2)按服务对象分类 序 号 服务 对象 三级模块 知识类型 地位、作用 1 通 识 模 块 人文概述 人文模块 通过人文概述,让学生能系统地了解 模块内容要学什么、为什么要学、怎 么去学 定积分的概念 基础模块 定积分的理论基础 定积分的几何意义和性 质 基础模块 定积分的理论基础、求平面图形的面 积的理论基础 变上限积分函数及其导 数 基础模块 微积分基本定理的基础、求带变限函 数积分极限的基础 微积分基本定理 基础模块 定积分计算的理论基础 不定积分的概念和基本 积分公式 基础模块 定积分计算的基础 微元法 基础模块 定积分用于处理实际问题的理论原 理 利用不定积分的性质计 算简单的不定积分 计算模块 用于计算简单的不定积分 凑微分法 计算模块 (不)定积分的常用计算方法 第二换元法(一)、(二) 计算模块 (不)定积分的常用计算方法 分部积分法(一)、(二) 计算模块 (不)定积分的常用计算方法 三角函数的积分 计算模块 用于计算有关三角函数的积分 平面图形的面积 应用模块 定积分的几何应用之一 专 业 定积分中的重要结论 基础模块 有理函数的积分 计算模块
服 可化为有理函数的积分 计算模块 务模 无穷区间上的广复积分 计算榄块 无界函数的广义积分 计算模块 块 利用变上限积分函数的 应用模块 导数求极限 2 利用量值积分售计误差 应用模块 专业学习雷要 立体的体积 应用横块 定积分的几何应用之一 曲线的弧长 应用榄块 定积分的几何应用之一 应用模块 给出了定积分在物理中处理问题的 定积分的物理应用 方法 定积分中的重要结论 基础榄块 深度常握。为考研服务 (奇属性、周期性) 有理函数的积分 计算横块 深度掌握。为考研服务 个 可化为有理函数的积分 计算模块 深度掌挥,为考研服务 性 无穷区间上的广复积分 计算榄块 深度掌握。为考研服务 化 无界函数的广义积分 计算横块 深度掌握。为考研服务 3 学 利用变上限积分函数的 模 导数求极限 应用核块 深度掌握。为考研服务 平面图形的面积 应用模块 深度掌握。为考研服务 旋转体的体 应用模块 深度掌握。为考研服务 曲线的氧长 应用枫块 深度掌握。为考研服务 定积分的物理应用 应用模块 深度掌挥。为考研服务 第五章常微分方程 (1)按知识类型分类 序 知识 号 类型 三级模块 教学要求 掌捏程度 人文 让学生大致了解常微分方程的起源与 常微分方程 了解 模块 发展,了解常微分方程的应用 理解微分方程的概念、微分方程的阶 基 数:在了解高阶微分方程餐念的基础 础 微分方程的基本概念 上,熟记求解微分方程的通解、特解以 然记 知 2 识 及初值日思的方法 熟悉线性齐次,丰齐次微分方程的通 线性微分方程解的站 块 解:了解用常数变易法求解华齐次微分 然悉 构 方程通解 -20-
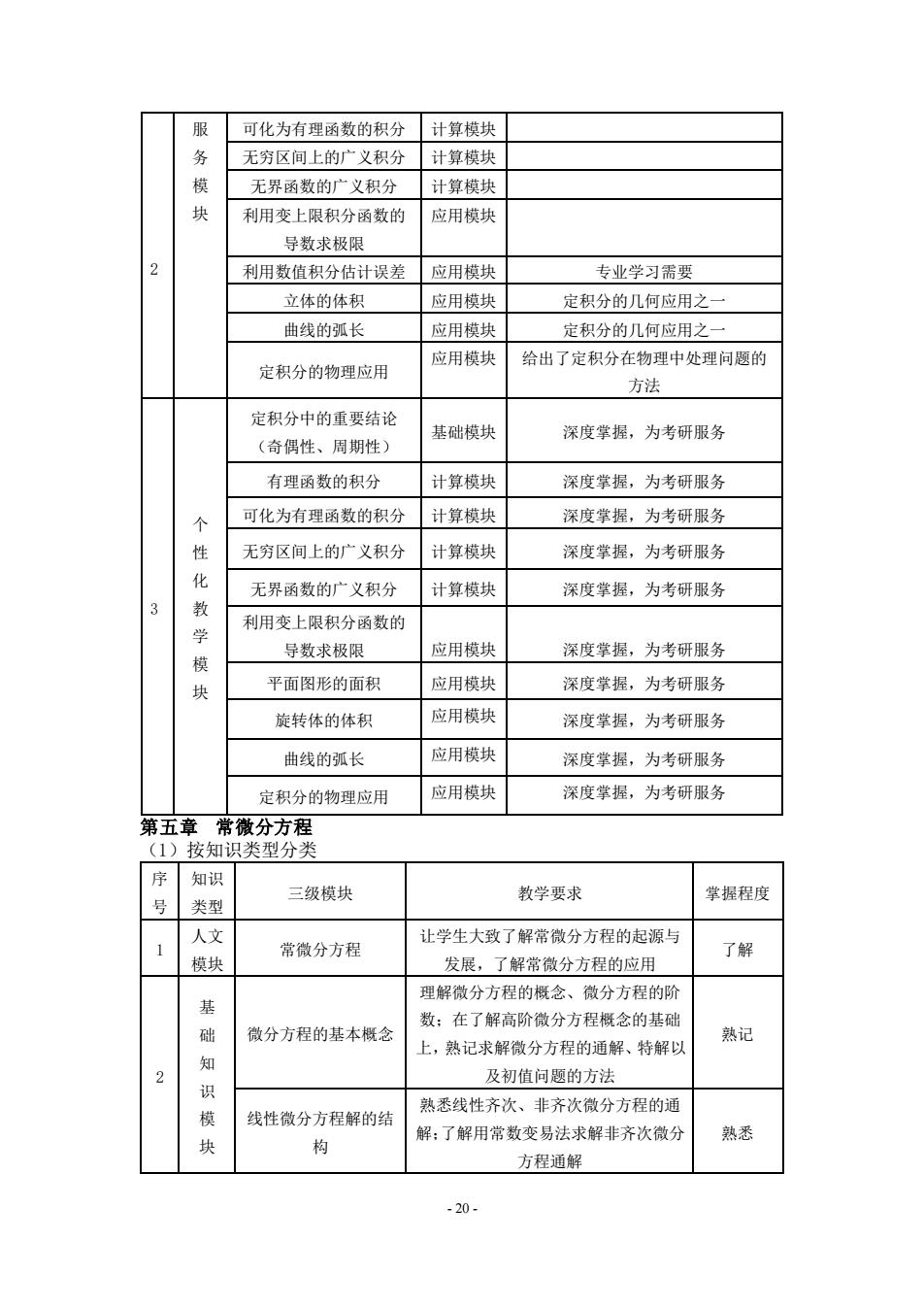
- 20 - 2 服 务 模 块 可化为有理函数的积分 计算模块 无穷区间上的广义积分 计算模块 无界函数的广义积分 计算模块 利用变上限积分函数的 导数求极限 应用模块 利用数值积分估计误差 应用模块 专业学习需要 立体的体积 应用模块 定积分的几何应用之一 曲线的弧长 应用模块 定积分的几何应用之一 定积分的物理应用 应用模块 给出了定积分在物理中处理问题的 方法 3 个 性 化 教 学 模 块 定积分中的重要结论 (奇偶性、周期性) 基础模块 深度掌握,为考研服务 有理函数的积分 计算模块 深度掌握,为考研服务 可化为有理函数的积分 计算模块 深度掌握,为考研服务 无穷区间上的广义积分 计算模块 深度掌握,为考研服务 无界函数的广义积分 计算模块 深度掌握,为考研服务 利用变上限积分函数的 导数求极限 应用模块 深度掌握,为考研服务 平面图形的面积 应用模块 深度掌握,为考研服务 旋转体的体积 应用模块 深度掌握,为考研服务 曲线的弧长 应用模块 深度掌握,为考研服务 定积分的物理应用 应用模块 深度掌握,为考研服务 第五章 常微分方程 (1)按知识类型分类 序 号 知识 类型 三级模块 教学要求 掌握程度 1 人文 模块 常微分方程 让学生大致了解常微分方程的起源与 发展,了解常微分方程的应用 了解 2 基 础 知 识 模 块 微分方程的基本概念 理解微分方程的概念、微分方程的阶 数;在了解高阶微分方程概念的基础 上,熟记求解微分方程的通解、特解以 及初值问题的方法 熟记 线性微分方程解的结 构 熟悉线性齐次、非齐次微分方程的通 解;了解用常数变易法求解非齐次微分 方程通解 熟悉