
西斜迟学院 Jiangxi University of Technology 理科教学部 《高等数学A》课程模块化教学大纲 (统招本科) 通用范困:款掌改革试点班级 2014年8月
理科教学部 《高等数学 A》课程模块化教学大纲 (统招本科) 适用范围:教学改革试点班级 2014 年 8 月
《高等数学A》课程模块化教学大纲 一、课程基本信息 课程名带 高等煮华A 课程英文名称 Higher mathenatics A 上争 总学时数 135 设 习题 6、观 授课 实贱 实验 计 123 0 0 课 12 4/周: 学时 学时 学时 学 学分 9 时 下争 时 期4/ 周 开课单位 江百科技学院理科教学郁 类型、层次 统招、本利 适用龙图 餐学改革试点班级 先修课整 初等数学基础 课松典别 学科通识课 选用教材 《微积分》,机械工餐出版社,张润确,陈一宏主编 L.《高等数学》(第三版),黄立宏主编,复旦大学出版社, 主要教学 2《高等数学》(第六版),问济大学数学系编,高等表育出版社。 参考号 3《微积分》,金路,北京大学出板杜, 高等数学是理工科学生各专业的必修课,通垃对高等数学内客的亚辑重组,强调 本深程 了知识的应用性,在数学教学中不仅要强化学生必要的计算能力,结合数学建模思想 任务和 培恭学生应用数学细识解决实际问思的能力,还晏侵高他们的数学修养,养成良好的 目的 思性品格。学生学好了高等数学。电为后燃各专业学习准备了数学知识,般炼和提高 了分析问题和解决问题的能力,有利子高素质人才的墙养, 教学大钢 数学教研室 数学大钢制订时间 2014.8 制可单位 二、课程内容及基本要求 极服棋块 瀑程内容: 一元函数部分
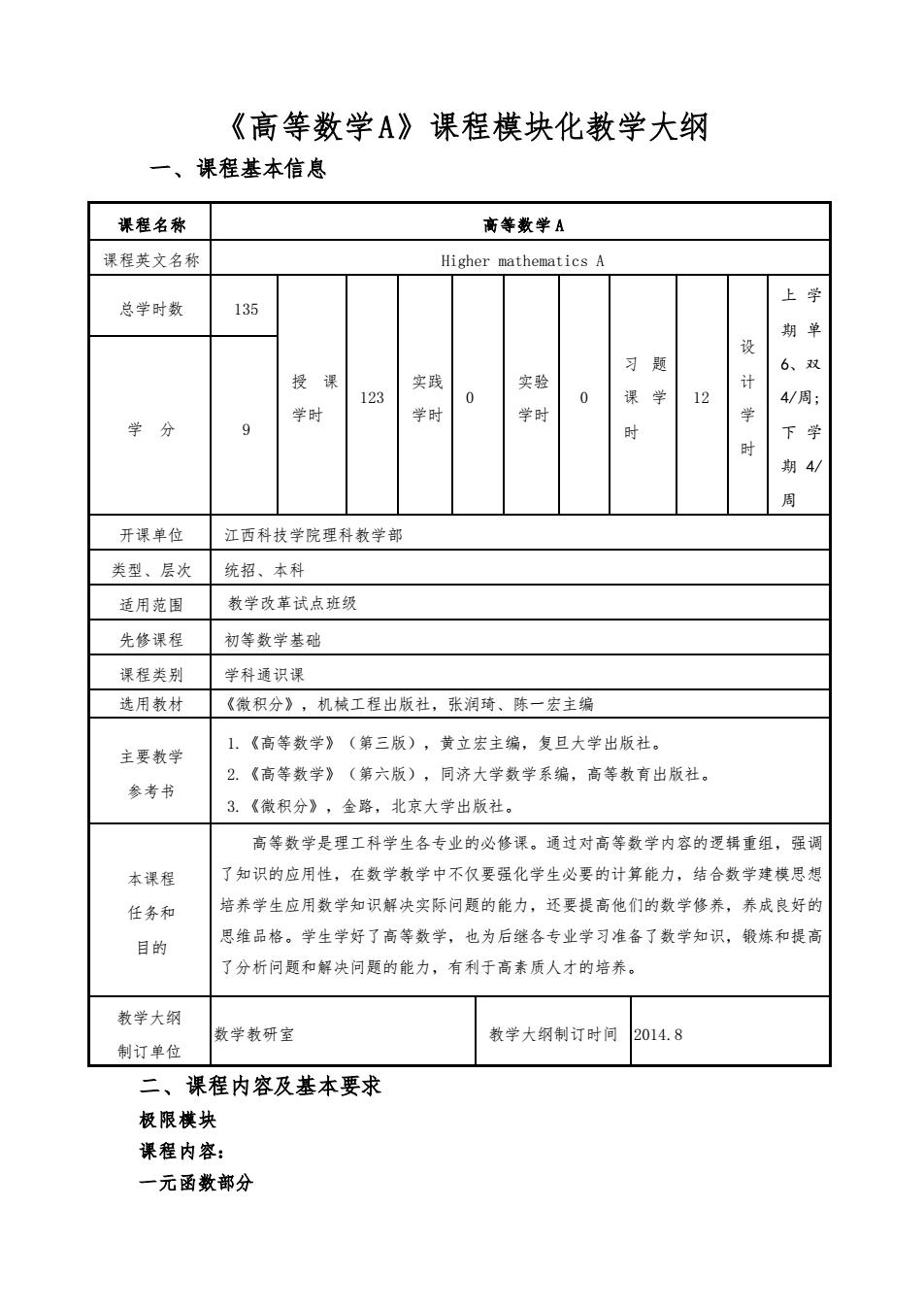
《高等数学 A》课程模块化教学大纲 一、课程基本信息 二、课程内容及基本要求 极限模块 课程内容: 一元函数部分 课程名称 高等数学 A 课程英文名称 Higher mathematics A 总学时数 135 授 课 学时 123 实践 学时 0 实验 学时 0 习 题 课 学 时 12 设 计 学 时 上 学 期 单 6、双 4/周; 下 学 期 4/ 周 学 分 9 开课单位 江西科技学院理科教学部 类型、层次 统招、本科 适用范围 教学改革试点班级 先修课程 初等数学基础 课程类别 学科通识课 选用教材 《微积分》,机械工程出版社,张润琦、陈一宏主编 主要教学 参考书 1.《高等数学》(第三版),黄立宏主编,复旦大学出版社。 2.《高等数学》(第六版),同济大学数学系编,高等教育出版社。 3.《微积分》,金路,北京大学出版社。 本课程 任务和 目的 高等数学是理工科学生各专业的必修课。通过对高等数学内容的逻辑重组,强调 了知识的应用性,在数学教学中不仅要强化学生必要的计算能力,结合数学建模思想 培养学生应用数学知识解决实际问题的能力,还要提高他们的数学修养,养成良好的 思维品格。学生学好了高等数学,也为后继各专业学习准备了数学知识,锻炼和提高 了分析问题和解决问题的能力,有利于高素质人才的培养。 教学大纲 制订单位 数学教研室 教学大纲制订时间 2014.8

1.数列的概念 2,函数的极限 3.极限的运算法则 4.两个重妥校限 5.无穷小与无穷大 6.函数的连续性 多元函数部分 7,多元函数的根限与连续 基本要求: 1,人文模块:了解极限思想的起源与发展。 2.基础模块:了解数列极限的定文:理解数列板限的性质、收数准则:了解函数 极限的定义:理解函数极限的性质。 3.计算能力模块:熟练掌樱极限的四则运算法则:理解极限存在的两个准则,并 利用它们求授限的方法:熟练掌握0/0型和D/0型未定式授限及变形式的求法:理 解无穷小,无穷大以及无穷小的阶的概金:熟练掌握无穷小的运算:熟练掌摆两个重 要授限及利用两个重要极限求授限的方法:掌握幂指函数极限的求法。 4,应用模块:理解函数的连续性。连续函数的基本性质和闭区间上连续函数的性 质:了解函数的同断点及判别间断点类型的方法:了解撒分学和积分学中的极限,以 及极限思想在其他领城中的应用。 5,延伸部分:了解多元函数的概念和二元函数的几何意义:理解二元函数的极限 与连续性的概念,以及有界闭区城上的连续函数的性质:会求二元函数的极限 重点:极限的四则运算法则:两个重要极限:无穷小及无穷小的比较:二元函数的根 限。 雅点:左授限与右授限概念及应用:极限存在的两个准则的应用:函数连续性:闭区 何上连续函数的性质:问断点及其分类:二元函数的极限与连续性的概念。 徽分棋块 课程内容: 一元函数都分 1,导数的概念 2.求导法则和求导基本公式 3.隐函数和参数方程确定的函数的导数 4.高阶导数 5.孟数的微分
1.数列的概念 2.函数的极限 3.极限的运算法则 4.两个重要极限 5.无穷小与无穷大 6.函数的连续性 多元函数部分 7.多元函数的极限与连续 基本要求: 1.人文模块:了解极限思想的起源与发展。 2.基础模块:了解数列极限的定义;理解数列极限的性质、收敛准则;了解函数 极限的定义;理解函数极限的性质。 3.计算能力模块:熟练掌握极限的四则运算法则;理解极限存在的两个准则,并 利用它们求极限的方法;熟练掌握 0/0 型和 / 型未定式极限及变形式的求法;理 解无穷小、无穷大以及无穷小的阶的概念;熟练掌握无穷小的运算;熟练掌握两个重 要极限及利用两个重要极限求极限的方法;掌握幂指函数极限的求法。 4.应用模块:理解函数的连续性、连续函数的基本性质和闭区间上连续函数的性 质;了解函数的间断点及判别间断点类型的方法;了解微分学和积分学中的极限,以 及极限思想在其他领域中的应用。 5.延伸部分:了解多元函数的概念和二元函数的几何意义;理解二元函数的极限 与连续性的概念,以及有界闭区域上的连续函数的性质;会求二元函数的极限。 重点:极限的四则运算法则;两个重要极限;无穷小及无穷小的比较;二元函数的极 限。 难点:左极限与右极限概念及应用;极限存在的两个准则的应用;函数连续性;闭区 间上连续函数的性质;间断点及其分类;二元函数的极限与连续性的概念。 微分模块 课程内容: 一元函数部分 1.导数的概念 2.求导法则和求导基本公式 3.隐函数和参数方程确定的函数的导数 4.高阶导数 5.函数的微分

6.微分中值定理 7.来定式的极 8.▲泰勒公式 9.函数性态的研究 10,曲线的曲率 11,▲方程的近似解 多元函数部分 12.偏导数 13.全微分 14.复合函数与隐函数的徽分法 15,方向导数与梯度 16,微分学在几何上的应用 17.▲二元函数的泰勒公式 18.多元函数的极值 基本要求: 1,人文模块:了解导数概念的起漂与发展:了解微分中值定理的内涵与作用。 2基础模块:理解导数的相关概念;理解导数的变化率意义:理解微分的概念: 了解曲率的概念:了解微分中值定理:理解偏导数的概念:了解全微分的概念;理解 方向导数及梯度的凝念。 3.计算能力模块:熟练掌握基本求导公式反导数的四则运算法则:掌提参数方程 求导法:掌握隐函数求导法及对数求导法:掌握洛必达法则:掌握偏导数的筒单计算: 熟练掌提复合函数微分法;掌摆隐函数澈分法:会求方向导数和梯度。 4,应用模块:掌握函数性态与导数的积暴:会求筒单的最值应用问题:理解微分 及全徽分的近假计算应用:掌握空问由找的切线与法平面的求法:掌樱曲面的切平面 与法线的求法:掌握多元函数的极值求法 5.廷仲部分:了解泰勒公式在计算方面的筒单应用:了解方程求近似解的基本方 法。 重点:导数的四则运算法则和复合函数的求导法则:基本初等函数的导数公式:隐函 数和由参数方程确定的函数的导数:掌强用导数判断函数的单调性和求极值的方法, 掌握函数最大值和最小值的求法:掌握用洛必达法则求未定式极限的方法:会用导数 判断函数图形的回凸性和锡点:函数的偏导数:方向导数与梯度的概念及其计算:多 元复合函数偏导数:隐函数的偏导数:由线的切线和法平面及由面的切平面和法线: 多元函数极值和条件授值的求法。 难点:微分的概念,复合函数的求导法则;分段函数的导数:反函数的导数:隐函数
6.微分中值定理 7.未定式的极限 8.▲泰勒公式 9.函数性态的研究 10.曲线的曲率 11.▲方程的近似解 多元函数部分 12.偏导数 13.全微分 14.复合函数与隐函数的微分法 15.方向导数与梯度 16.微分学在几何上的应用 17.▲二元函数的泰勒公式 18.多元函数的极值 基本要求: 1.人文模块:了解导数概念的起源与发展;了解微分中值定理的内涵与作用。 2.基础模块:理解导数的相关概念;理解导数的变化率意义;理解微分的概念; 了解曲率的概念;了解微分中值定理;理解偏导数的概念;了解全微分的概念;理解 方向导数及梯度的概念。 3.计算能力模块:熟练掌握基本求导公式及导数的四则运算法则;掌握参数方程 求导法;掌握隐函数求导法及对数求导法;掌握洛必达法则;掌握偏导数的简单计算; 熟练掌握复合函数微分法;掌握隐函数微分法;会求方向导数和梯度。 4.应用模块:掌握函数性态与导数的联系;会求简单的最值应用问题;理解微分 及全微分的近似计算应用;掌握空间曲线的切线与法平面的求法;掌握曲面的切平面 与法线的求法;掌握多元函数的极值求法。 5.延伸部分:了解泰勒公式在计算方面的简单应用;了解方程求近似解的基本方 法。 重点:导数的四则运算法则和复合函数的求导法则;基本初等函数的导数公式;隐函 数和由参数方程确定的函数的导数;掌握用导数判断函数的单调性和求极值的方法, 掌握函数最大值和最小值的求法;掌握用洛必达法则求未定式极限的方法;会用导数 判断函数图形的凹凸性和拐点;函数的偏导数;方向导数与梯度的概念及其计算;多 元复合函数偏导数;隐函数的偏导数;曲线的切线和法平面及曲面的切平面和法线; 多元函数极值和条件极值的求法。 难点:微分的概念,复合函数的求导法则;分段函数的导数;反函数的导数;隐函数

和由参数方程确定的导数:函数最大值和最小值的求法及其筒单应用:用洛必达法则 求来定式极限的方法:柯西中值定理:利用导数判断函数图形的四凸性和拐点:全微 分形式的不变性:复台函数偏导数的求法:二元函数的二阶泰勒公式:隐函数的偏导 数:拉格朗日乘数法:多元函数的最大值和最小值, 补充内容:“微分学在几何上的应用”这节以向量代数与空问解析几何中的内容为 基础,需要在讲授本节之前加入以下内客:空何直角坐标系:向量及其线性适算:向 量的来积:平面的方程:空问直线的方程和空问曲面与空问曲线。 积分棋块 课程内容: 一元函数都分 1.炭积分的概念反性质 2.微积分基本公式 3.不定积分 4.定积分的计算 5.▲广义积分 6.★定积分的几何应用 7.★定积分的物理应用 多元函数部分 8.重积分的概念和性质 9.二重积分的计算 10.三重积分的计算 11,★重积分的应用 12.▲重积分的换元法 13.第一类(对氟长的)曲绿积分 14.第二类(对坐标的)曲线积分 16.格林公式平面由线积分与路径无美的条件 17.第一类(对面积的)曲面积分 18.▲第二类(对坐标的)曲面积分 19.★高斯公式与数度 20.★斯托克斯公式与旋度 基本要求: 1,人文模块:了解积分产生的人文背景。 2.基础模块:理解定积分的概念及性质、定积分的几何意义:理解源函数与不定
和由参数方程确定的导数;函数最大值和最小值的求法及其简单应用;用洛必达法则 求未定式极限的方法;柯西中值定理;利用导数判断函数图形的凹凸性和拐点;全微 分形式的不变性;复合函数偏导数的求法;二元函数的二阶泰勒公式;隐函数的偏导 数;拉格朗日乘数法;多元函数的最大值和最小值。 补充内容:“微分学在几何上的应用”这节以向量代数与空间解析几何中的内容为 基础,需要在讲授本节之前加入以下内容:空间直角坐标系;向量及其线性运算;向 量的乘积;平面的方程;空间直线的方程和空间曲面与空间曲线。 积分模块 课程内容: 一元函数部分 1.定积分的概念及性质 2.微积分基本公式 3.不定积分 4.定积分的计算 5.▲广义积分 6.★定积分的几何应用 7.★定积分的物理应用 多元函数部分 8.重积分的概念和性质 9.二重积分的计算 10.三重积分的计算 11.★重积分的应用 12.▲重积分的换元法 13.第一类(对弧长的)曲线积分 14.第二类(对坐标的)曲线积分 16.格林公式 平面曲线积分与路径无关的条件 17.第一类(对面积的)曲面积分 18.▲第二类(对坐标的)曲面积分 19.★高斯公式与散度 20.★斯托克斯公式与旋度 基本要求: 1.人文模块:了解积分产生的人文背景。 2.基础模块:理解定积分的概念及性质、定积分的几何意义;理解原函数与不定