
2.3控制系统的复域数学模型 控制系统的微分方程是在时间域描述系统动态性能的数学模型,在给定外作用及初始条 件下,求解微分方程可以得到系统输出响应的全部时间信息。这种方法直观、准确,但是如 果系统的结构改变或某个参数变化时,就要重新列写并求解微分方程,不便于对系统分析和 设计。 传递函数是在拉氏变换基础上的复数域中的数学模型。传递函数不仅可以表征系统的动 态特性,而且可以用来研究系统的结构或参数变化对系统性能的影响。经典控制理论中广泛 应用的根轨迹法和频域法,就是以传递函数为基础建立起来的,因此传递函数是经典控制理 论中最基本也是最重要的数学模型。 2.3.1传递函数 1.传递函数的定义 传递函数是在零初始条件下,线性定常系统输出量的拉氏变换与输入量的拉氏变换之 比。 线性定常系统的微分方程一般为 a.ddd)a de()()= al" d司 al 0t+0+0 (2-25) d 式中:c(0为输出:)为输入量:a,an1,a及bn,b1b均为由系统结构、参 数决定的常系数。 在零初始条件下对式(2-25)两端进行拉氏变换,可得相应的代数方程 (a,s+an3+.+a3+a)C(s)=(bns"+bms1++bs+b)R(s)(2-26) 系统的传递函数为 C⊙_b+bS1++65+6=G6 R(s)a,5"+a1s-l+.…+a,5+a0 (2-27)
22 2.3 控制系统的复域数学模型 控制系统的微分方程是在时间域描述系统动态性能的数学模型,在给定外作用及初始条 件下,求解微分方程可以得到系统输出响应的全部时间信息。这种方法直观、准确,但是如 果系统的结构改变或某个参数变化时,就要重新列写并求解微分方程,不便于对系统分析和 设计。 传递函数是在拉氏变换基础上的复数域中的数学模型。传递函数不仅可以表征系统的动 态特性,而且可以用来研究系统的结构或参数变化对系统性能的影响。经典控制理论中广泛 应用的根轨迹法和频域法,就是以传递函数为基础建立起来的,因此传递函数是经典控制理 论中最基本也是最重要的数学模型。 2.3.1 传递函数 1.传递函数的定义 传递函数是在零初始条件下,线性定常系统输出量的拉氏变换与输入量的拉氏变换之 比。 线性定常系统的微分方程一般为 1 1 1 0 1 1 1 1 0 1 ( ) ( ) ( ) ... ( ) ( ) ( ) ( ) ... ( ) n n n n n n m m m m m m d c t d c t dc t a a a a c t dt dt dt d r t d r t dr t b b b b r t dt dt dt − − − − − − + + + + = + + + + (2-25) 式中: ct() 为输出; rt() 为输入量; 1 0 an , an− ,...,a 及 1 0 bm , bm− ,...,b 均为由系统结构、参 数决定的常系数。 在零初始条件下对式(2-25)两端进行拉氏变换,可得相应的代数方程 1 1 1 1 0 1 1 0 ( .... ) ( ) ( ... ) ( ) n n m m n n m m a s a s a s a C s b s b s b s b R s − − + + + + = + + + + − − (2-26) 系统的传递函数为 ( ) ... ... ( ) ( ) 1 0 1 1 1 0 1 1 G s a s a s a s a b s b s b s b R s C s n n n n m m m m = + + + + + + + + = − − − − (2-27)

传递函数是在零初始条件下定义的。零初始条件有两方面含义:一是指输入作用是在 1=0以后才作用于系统,因此,系统输入量及其各阶导数在1≤0时均为零:二是指输入 作用于系统之前,系统是“相对静止”的,即系统输出量及各阶导数在1≤0时的值也为 零。大多数实际工程系统都满足这样的条件。零初始条件的规定不仅能简化运算,而且有利 于在同等条件下比较系统性能。所以,这样规定是必要的。 例2-6试求例2-1中的R-LC无源网络的传递函数。 解由例21式(2-3)可知RLC无源网络的微分方程为 在零初始条件下,对上式两端取拉氏变换并整理可得网络传递函数 Ou 实际求元部件传递函数时必须考虑负载效应,所求的传递函数应当反映元部件正常带载 时工作的特性。比如,电动机空载时的特性不能反映带载运行时的特性 2.传递函数的性质 ()传递函数是复变量5的有理分式,它具有复变函数的所有性质。因为实际物理系统 总是存在惯性,并且能源功率有限,所以实际系统传递函数的分母阶次总是大于或等于分 子阶次m,即n≥m。 (②)传递函数只取决于系统的结构参数,与外作用无关。 (3)传递函数与微分方程有直接联系。 ()传递函数的拉氏反变换即为系统的脉冲响应,因此传递函数能反映系统运动特性。 因为单位脉冲函数的拉氏变换式为1(即:R(s)=L[)=1),因此有 rkaolr}-kalao (2-28) 应当注意传递函数的局限性及适用范围。传递函数是从拉氏变换导出的,拉氏变换是 种线性变换,因此传递函数只适应于描述线性定常系统。传递函数是在零初始条件下定义的, 所以它不能反映非零初始条件下系统的自由响应运动规律。 2.3.2常用控制元件的传递函数 1.电位器
23 传递函数是在零初始条件下定义的。零初始条件有两方面含义:一是指输入作用是在 t = 0 以后才作用于系统,因此,系统输入量及其各阶导数在 t 0 时均为零;二是指输入 作用于系统之前,系统是“相对静止”的,即系统输出量及各阶导数在 t 0 时的值也为 零。大多数实际工程系统都满足这样的条件。零初始条件的规定不仅能简化运算,而且有利 于在同等条件下比较系统性能。所以,这样规定是必要的。 例 2-6 试求例 2-1 中的 R-L-C 无源网络的传递函数。 解 由例 2-1 式(2-3)可知 R-L-C 无源网络的微分方程为 ( ) ( ) ( ) ( ) 2 2 u t u t dt du t RC dt d u t LC c r c c + + = 在零初始条件下,对上式两端取拉氏变换并整理可得网络传递函数 1 1 ( ) ( ) ( ) 2 + + = = U s LCs RCs U s G s r c 实际求元部件传递函数时必须考虑负载效应,所求的传递函数应当反映元部件正常带载 时工作的特性。比如,电动机空载时的特性不能反映带载运行时的特性。 2.传递函数的性质 ⑴ 传递函数是复变量 s 的有理分式,它具有复变函数的所有性质。因为实际物理系统 总是存在惯性,并且能源功率有限,所以实际系统传递函数的分母阶次 n 总是大于或等于分 子阶次 m,即 n≥m。 ⑵ 传递函数只取决于系统的结构参数,与外作用无关。 ⑶ 传递函数与微分方程有直接联系。 ⑷ 传递函数的拉氏反变换即为系统的脉冲响应,因此传递函数能反映系统运动特性。 因为单位脉冲函数的拉氏变换式为 1(即: R s L t ( ) ( ) 1 = = ),因此有 ( ) ( ) ( ) ( ) ( ) 1 1 1 L C s k t R s C s L G s L = = = − − − (2-28) 应当注意传递函数的局限性及适用范围。传递函数是从拉氏变换导出的,拉氏变换是一 种线性变换,因此传递函数只适应于描述线性定常系统。传递函数是在零初始条件下定义的, 所以它不能反映非零初始条件下系统的自由响应运动规律。 2.3.2 常用控制元件的传递函数 1.电位器
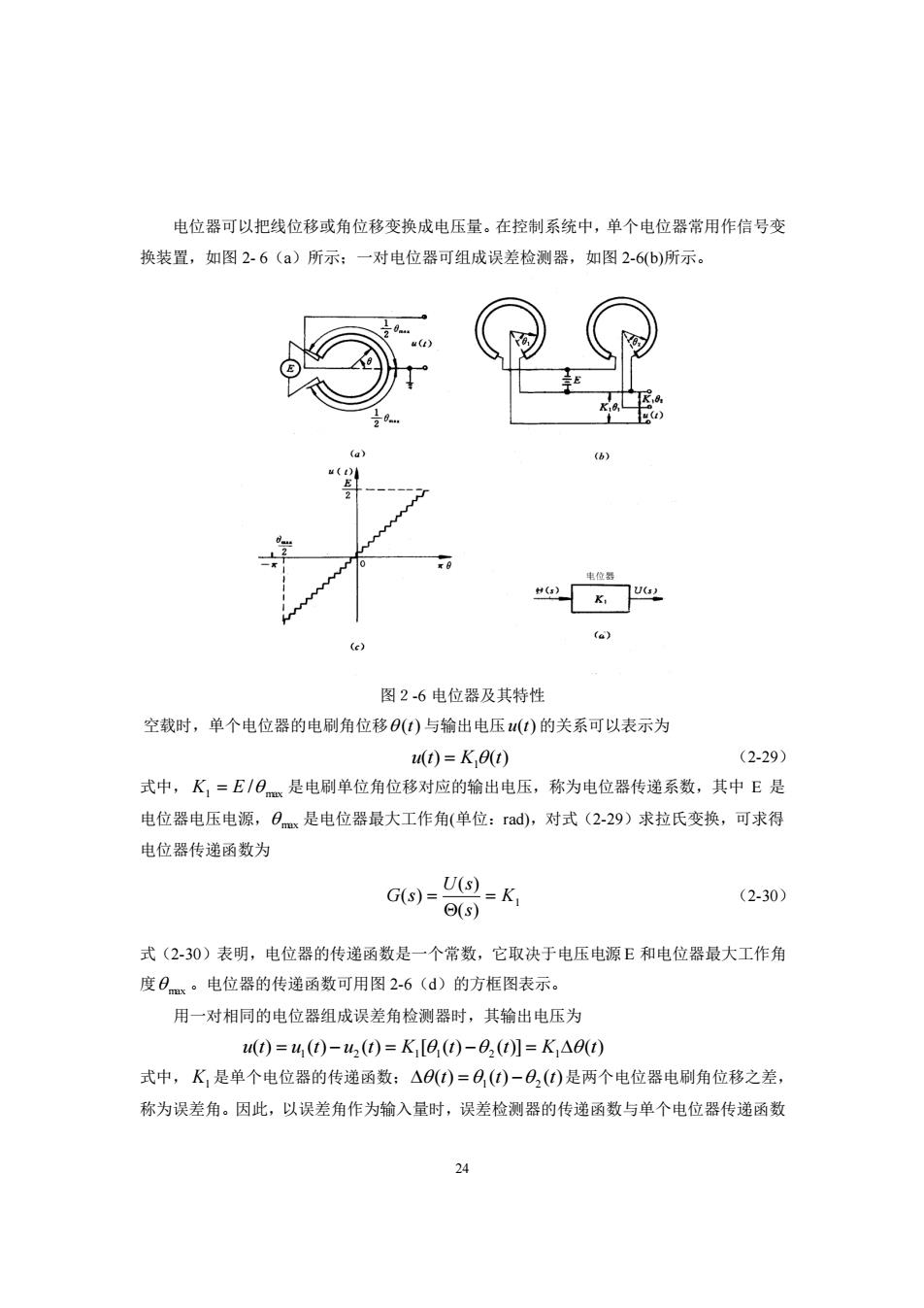
电位器可以把线位移或角位移变换成电压量。在控制系统中,单个电位器常用作信号变 换装置,如图2-6(a)所示:一对电位器可组成误差检测器,如图2-6(b)所示。 () 位器 四K☐ fu) 图2-6电位器及其特性 空载时,单个电位器的电刷角位移()与输出电压()的关系可以表示为 u(1)=K 0(1) (2-29) 式中,K,=E/日是电刷单位角位移对应的输出电压,称为电位器传递系数,其中E是 电位器电压电源,日m是电位器最大工作角(单位:rad,对式(2-29)求拉氏变换,可求得 电位器传递函数为 Gs)=y 5 (2-30) 式(230)表明,电位器的传递函数是一个常数,它取决于电压电源E和电位器最大工作角 度0x。电位器的传递函数可用图2-6(d)的方框图表示。 用一对相同的电位器组成误差角检测器时,其输出电压为 4)=40-4(0=K[0,(0-0()=K,△0) 式中,K是单个电位器的传递函数:△(t)=O(t)-O,()是两个电位器电刷角位移之差, 称为误差角。因此,以误差角作为输入量时,误差检测器的传递函数与单个电位器传递函数 2
24 电位器可以把线位移或角位移变换成电压量。在控制系统中,单个电位器常用作信号变 换装置,如图 2- 6(a)所示;一对电位器可组成误差检测器,如图 2-6(b)所示。 图2-6 电位器及其特性 空载时,单个电位器的电刷角位移 (t) 与输出电压 u(t) 的关系可以表示为 ( ) ( ) 1 u t = K t (2-29) 式中, 1 max K = E / 是电刷单位角位移对应的输出电压,称为电位器传递系数,其中 E 是 电位器电压电源, max 是电位器最大工作角(单位:rad),对式(2-29)求拉氏变换,可求得 电位器传递函数为 1 ( ) ( ) ( ) K s U s G s = = (2-30) 式(2-30)表明,电位器的传递函数是一个常数,它取决于电压电源 E 和电位器最大工作角 度 max 。电位器的传递函数可用图 2-6(d)的方框图表示。 用一对相同的电位器组成误差角检测器时,其输出电压为 ( ) ( ) ( ) [ ( ) ( )] ( ) 1 2 1 1 2 1 u t = u t −u t = K t − t = K t 式中, K1 是单个电位器的传递函数; ( ) ( ) ( ) 1 2 t = t − t 是两个电位器电刷角位移之差, 称为误差角。因此,以误差角作为输入量时,误差检测器的传递函数与单个电位器传递函数

形式相同,即为 G==K (2-31) Ae(s) 在使用电位器时应注意其负载效应。负载效应是指在元部件输出端接有负载时所产生 的影响。图2-7表示电位器输出端接有负载电 阻R,时的电路图,设电位器电阻为R。,回 路电流为 E-u0_0+ u(s) Rp-Rp Rp R 整理可得电位器输出电压为 图28电位器的负载效应 u)= E0(t) = +R01-0] (2-32) R。R 可见,由于负载电阻R,的影响,输出电压)与电刷角位移()不再保持线性关系 如果负载电阻R,很大,例如,R210R,时,可以近似得到 (0≈E0)/0m=K,)。 2.自整角机 自整角机由一个发送器和一个接收器(也称控制变压器)组成,其原理图及连接方法如 图2-8所示。它的工作原理如下。 在发送器的转子单相绕组上加上交流激磁电压e,()=Esnm后,在发送器上就产生 脉动磁通·,使定子三相绕组中产生电流,该电流在接收器中产生一脉动磁通女。当 0。=90°+0,时,转子绕组则不感应通中.,输出(0=0,当0.≠90°+0,时,克在接收 机转子绕组中产生感应电势(),其大小为 e(t)=K,cos(0,-0)sin ot (2-33) E K,-0,-00 (2-34) 式中K,一自整角机灵敏度(V/C): E一误差电压:
25 形式相同,即为 1 ( ) ( ) ( ) K s U s G s = = (2-31) 在使用电位器时应注意其负载效应。负载效应是指在元部件输出端接有负载时所产生 的影响。图 2-7 表示电位器输出端接有负载电 阻 RL 时的电路图,设电位器电阻为 Rp ,回 路电流为 ' ' ( ) ( ) ( ) P P P L E u t u t u t R R R R − = + − 整理可得电位器输出电压为 ' max ' max max ( ) ( ) ( ) ( ) (1 ) [1 (1 )] p p p p p L p L E E t u t R R R R t t R R R R = = + − + − (2-32) 可见,由于负载电阻 RL 的影响,输出电压 u(t) 与电刷角位移 (t) 不再保持线性关系, 如果负载电阻 RL 很大,例如, 10 R R L p 时,可以近似得到 ( ) ( )/ ( ) max 1 u t E t = K t 。 2.自整角机 自整角机由一个发送器和一个接收器(也称控制变压器)组成,其原理图及连接方法如 图 2-8 所示。它的工作原理如下。 在发送器的转子单相绕组上加上交流激磁电压 e (t) E sint 1 = 1 后,在发送器上就产生 脉动磁通 r ,使定子三相绕组中产生电流,该电流在接收器中产生一脉动磁通 c 。当 c = + r 90 时,转子绕组则不感应通 c ,输出 e(t) = 0 ,当 c + r 90 时, c 在接收 机转子绕组中产生感应电势 e(t) ,其大小为 e t K t ( ) = s cos( r − c )sin (2-33) r c e s E E K = − = (2-34) 式中 Ks —自整角机灵敏度( V C ); E —误差电压;
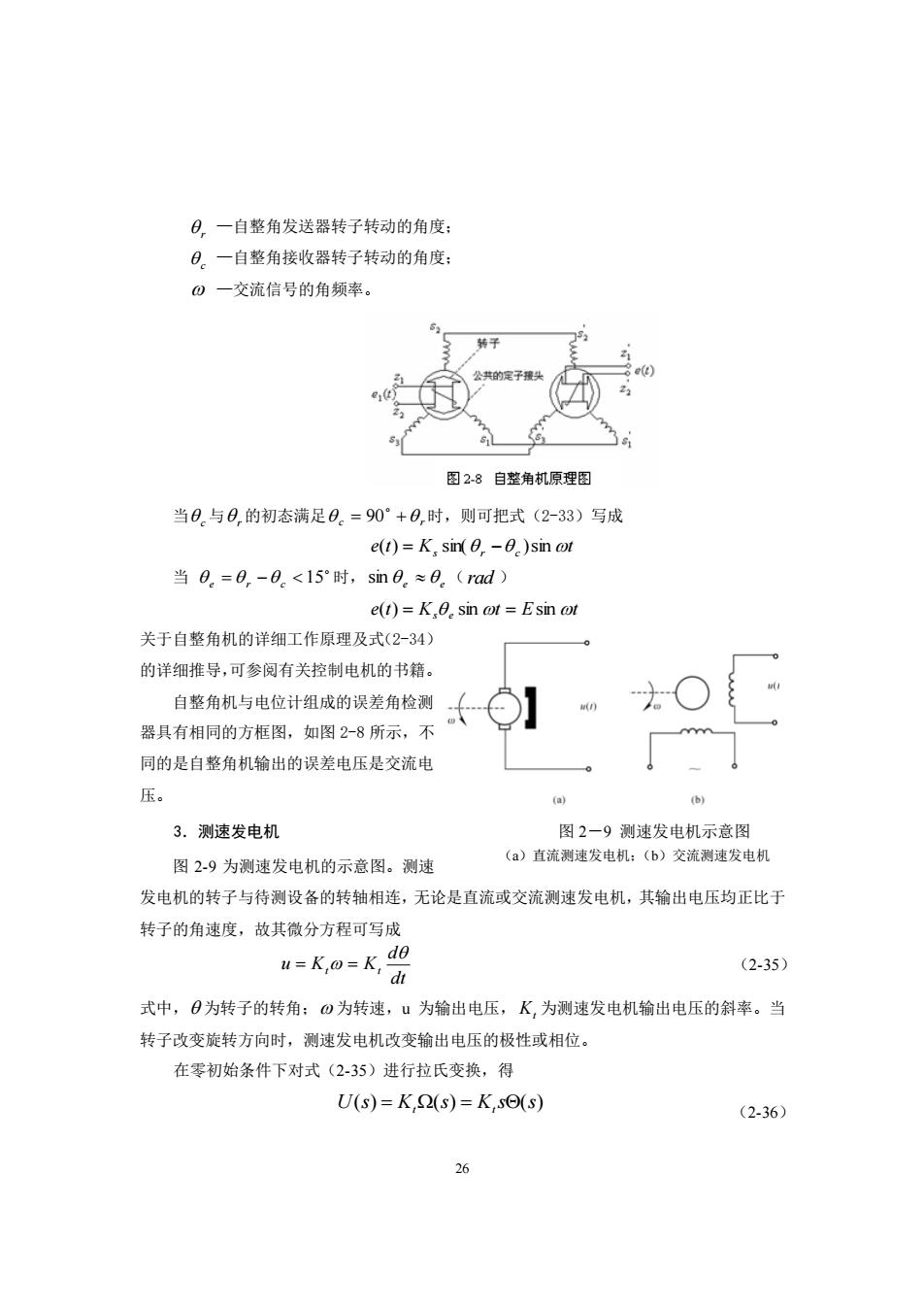
日,一自整角发送器转子转动的角度: 日。一自整角接收器转子转动的角度 0一交流信号的角频率。 子 图28自整角机原理图 当0。与0的初态满足0。=90°+0,时,则可把式(2-33)写成 e(t)=K.sin 0-0)sin oot 当0.=0,-0。<15°时,sin8.≈6。(rad) e(t)=K.0.sm ot Esin ot 关于自整角机的详细工作原理及式(234) 的详细推导,可参阅有关控制电机的书籍。 自整角机与电位计组成的误差角检测 器具有相同的方框图,如图2-8所示,不 同的是自整角机输出的误差电压是交流电 压。 a 3.测速发电机 图2一9测速发电机示意图 图2-9为测速发电机的示意图。测速 (a)直流测速发电机:(b)交流测速发电机 发电机的转子与待测设备的转轴相连,无论是直流或交流测速发电机,其输出电压均正比于 转子的角速度,故其微分方程可写成 I=Ko=水9 (2-35) 式中,O为转子的转角:0为转速,u为输出电压,K,为测速发电机输出电压的斜率。当 转子改变旋转方向时,测速发电机改变输出电压的极性或相位。 在零初始条件下对式(2-35)进行拉氏变换,得 U(s)=K,(s)=K,se(s) (2-36)
26 r —自整角发送器转子转动的角度; c —自整角接收器转子转动的角度; —交流信号的角频率。 当 c 与 r 的初态满足 c = + r 90 时,则可把式(2-33)写成 e t K t ( ) = s sin( r − c )sin 当 e = r − c 15 时, e e sin ( rad ) e t K t E t ( ) = s e sin = sin 关于自整角机的详细工作原理及式(2-34) 的详细推导,可参阅有关控制电机的书籍。 自整角机与电位计组成的误差角检测 器具有相同的方框图,如图 2-8 所示,不 同的是自整角机输出的误差电压是交流电 压。 3.测速发电机 图 2-9 为测速发电机的示意图。测速 发电机的转子与待测设备的转轴相连,无论是直流或交流测速发电机,其输出电压均正比于 转子的角速度,故其微分方程可写成 dt d u Kt Kt = = (2-35) 式中, 为转子的转角; 为转速,u 为输出电压, Kt 为测速发电机输出电压的斜率。当 转子改变旋转方向时,测速发电机改变输出电压的极性或相位。 在零初始条件下对式(2-35)进行拉氏变换,得 U(s) K (s) K s (s) = t = t (2-36) 图 2-9 测速发电机示意图 (a)直流测速发电机;(b)交流测速发电机