电工技术 2.1.31 电阻星形联结与三角形联结的等效变换 dlangong a 等效变换 al ca Y-→△ △>Y Rab Rca 星形网络中的每个电阻 等于三角形网络中两相邻 Rp Rpe Rab 支路电阻的乘积,除以三 Rab Rpe Rea 个三角形网络电阻的和。 R Rea Rpe Rap Roc +Rca 总目录章目录返回上一页下一页
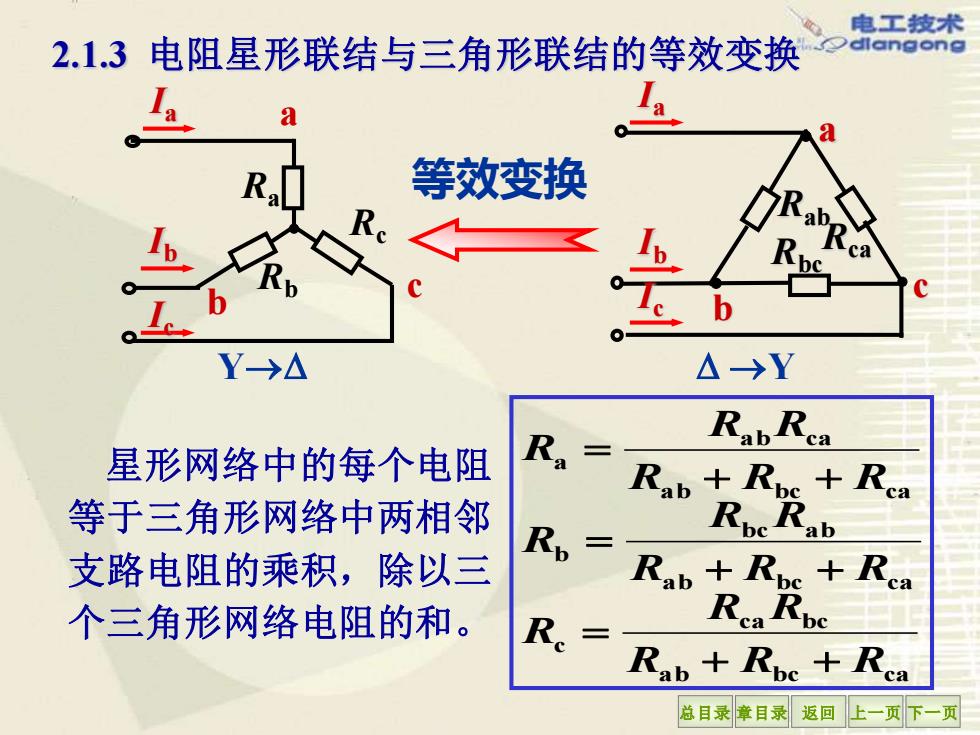
总目录 章目录 返回 上一页 下一页 a b bc ca ca bc c a b bc ca bc a b b a b bc ca a b ca a R R R R R R R R R R R R R R R R R R + + = + + = + + = Y→ →Y a 等效变换 a c b R Rca bc Rab Ia Ib Ic Ia Ib Ic b c Ra Rc Rb 2.1.3 电阻星形联结与三角形联结的等效变换 星形网络中的每个电阻 等于三角形网络中两相邻 支路电阻的乘积,除以三 个三角形网络电阻的和
电工技术 2.1.3 电阻星形联结与三角形联结的等效变换 a 等效变换 Rca b Y→△ △→Y 三角形网络中的每个电 Rb RaRb+RbR。+RRa R 阻等于星形网络中所有可 Rpe RRb+RbR。+RRa 能的两个电阻乘积的和, R. 除以相对的星形网络电阻。 RaRb+RbR。+RRa Rp 总目录章目录返回 上一页下一页
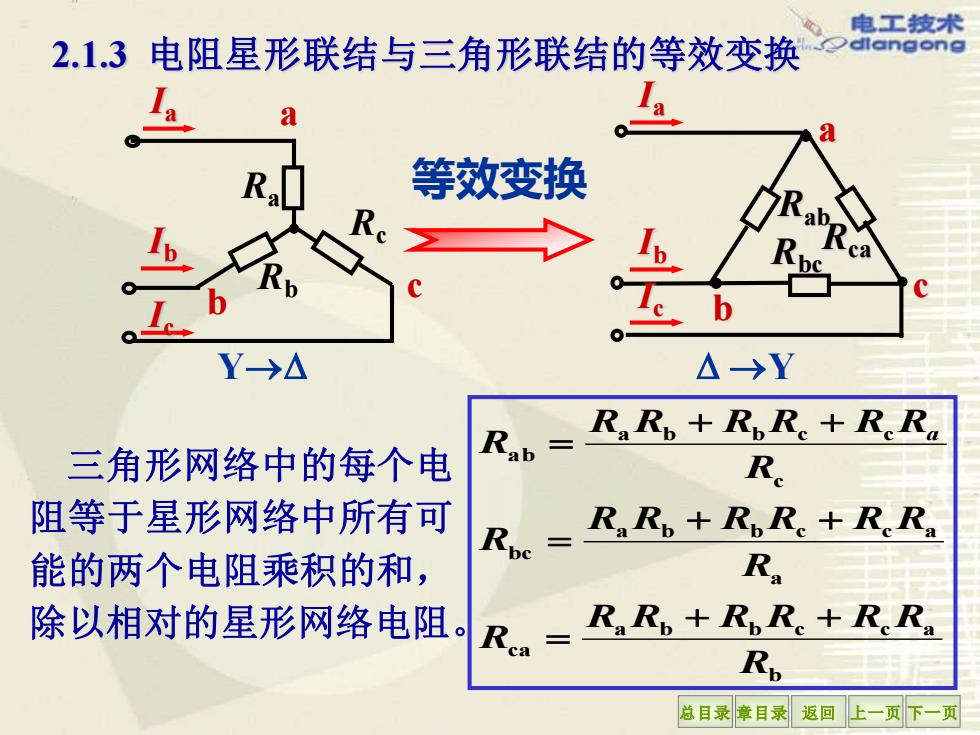
总目录 章目录 返回 上一页 下一页 b a b b c c a ca a a b b c c a bc c a b b c c a b R R R R R R R R R R R R R R R R R R R R R R R R a + + = + + = + + = Y→ →Y a 等效变换 a c b R Rca bc Rab Ia Ib Ic Ia Ib Ic b c Ra Rc Rb 2.1.3 电阻星形联结与三角形联结的等效变换 三角形网络中的每个电 阻等于星形网络中所有可 能的两个电阻乘积的和, 除以相对的星形网络电阻
电工技术 2.1.3电阻星形联结与三角形联结的等效变换 dlangong 等效变换 将Y形联接等效变换为△形联结时 若Ra=Rb=R。=R时,有Rab=Rb=Rca=RA=3R; 将△形联接等效变换为Y形联结时 若Rab=Rbc=Ra=R时,有R=Rb=R。=Ry=R3 总目录章目录返回上一页下一页
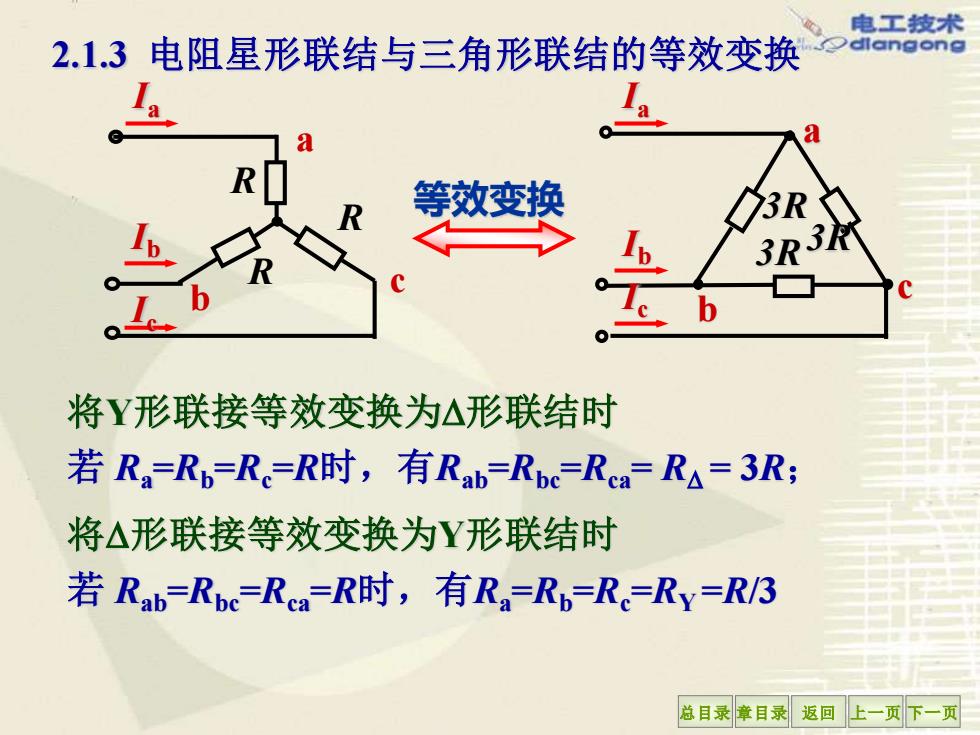
总目录 章目录 返回 上一页 下一页 将Y形联接等效变换为形联结时 若 Ra =Rb=Rc =R时,有Rab=Rbc=Rca= R = 3R; 将形联接等效变换为Y形联结时 若 Rab=Rbc=Rca =R时,有Ra =Rb=Rc =RY =R/3 等效变换 a c b 3R 3R 3R Ia Ib Ic Ia Ib Ic b c R R R a 2.1.3 电阻星形联结与三角形联结的等效变换
电工技术 例1:对图示电路求总电阻R12 dlangong 0.82 1 0.8 由图: 2.42 2.6842 R12-2.682 总目录章目录返回 上一页下一页
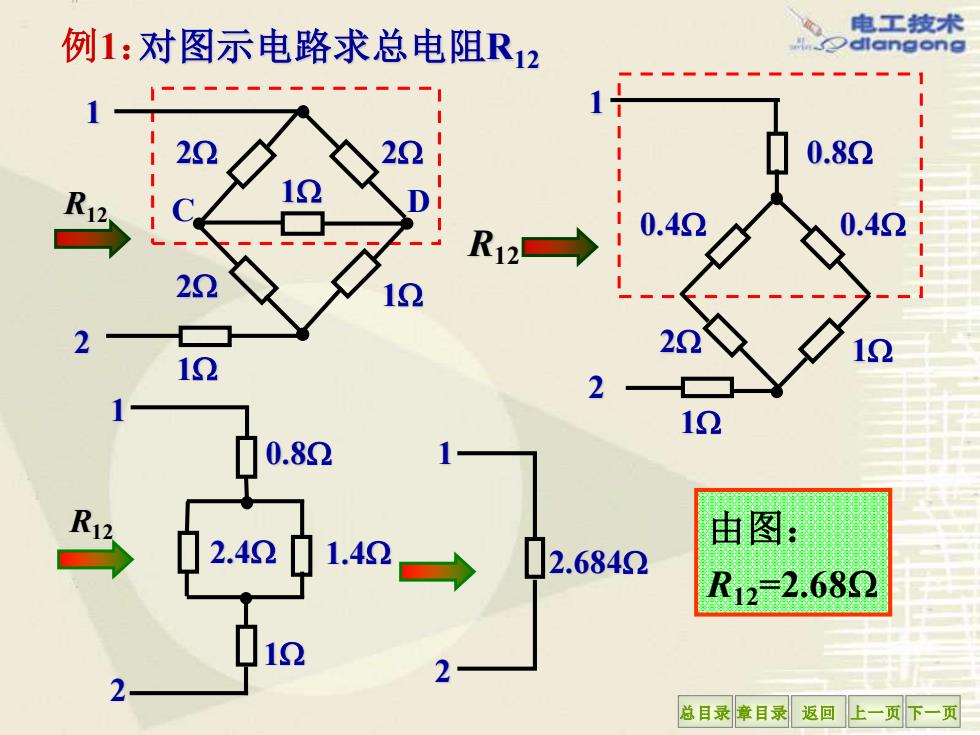
总目录 章目录 返回 上一页 下一页 例1:对图示电路求总电阻R12 R12 2 1 2 2 2 1 1 1 由图: R12=2.68 R12 C D 1 2 1 1 0.4 0.4 0.8 2 R12 1 0.8 2.4 1.4 1 2 1 2 2.684
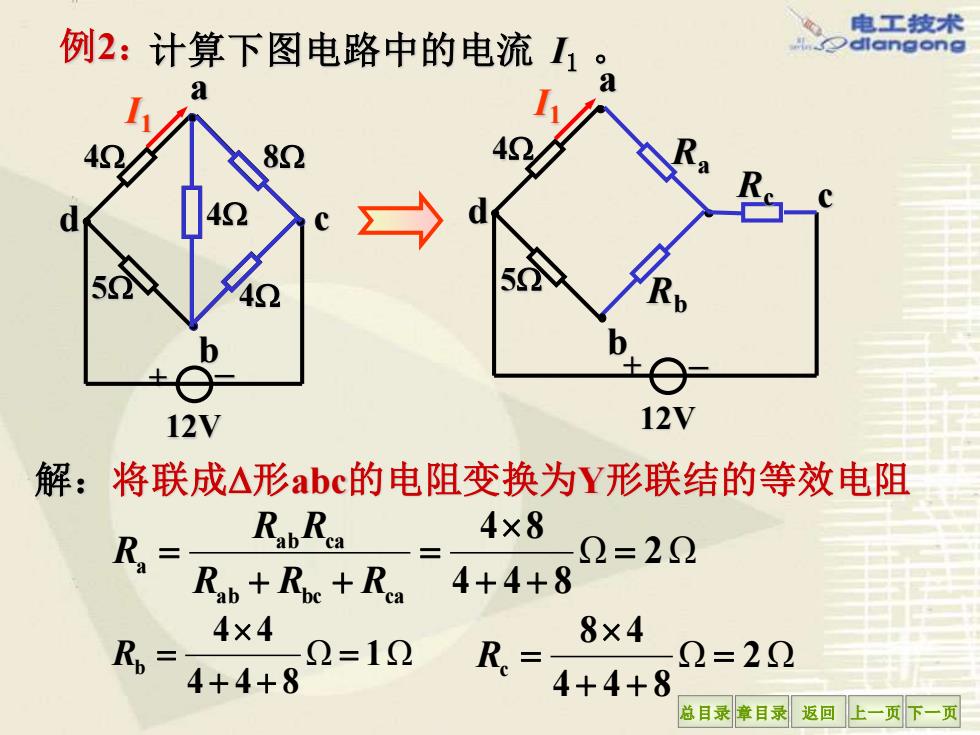
电工技术 例2:计算下图电路中的电流1。 dlangong a 12V 12V 解:将联成△形abc的电阻变换为Y形联结的等效电阻 4×8 R=- RaL Rca 2=22 Rab+Roe+Rca 4+4+8 4×4 2=10 8×4 Rp= 4+4+8 R= 2=22 4+4+8 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 例2:计算下图电路中的电流 I1 。 I1 + – 4 5 8 4 4 12V a b d c 解:将联成形abc的电阻变换为Y形联结的等效电阻 I1 + – 4 5 Ra Rb Rc 12V a b c d Ω 2 Ω 4 4 8 4 8 a b bc ca a b ca a = + + = + + = R R R R R R Ω 1Ω 4 4 8 4 4 b = + + R = Ω 2 Ω 4 4 8 8 4 c = + + R =