
1.1计算电磁学的产生背景 966 涉及电磁学的众多领域 > 计算电磁学与电磁场理论 √电磁场理论为计算电磁学提供电磁规律、 数学方程 √计算电磁学为电磁场理论提供运算方法和探索手段、计算数据 >计算电磁学与电磁场工程 √电磁场工程为计算电磁学提供实验验证、需求牵引 √计算电磁学为电磁场工程提供建模与仿真、优化与设计 >近三十年来 √电磁场理论的发展(探索未知) √电磁场工程的进步(需求牵引) √均与计算电磁学的发展密切相关 10
10 1.1 计算电磁学的产生背景 涉及电磁学的众多领域 计算电磁学与电磁场理论 电磁场理论为计算电磁学提供电磁规律、数学方程 计算电磁学为电磁场理论提供运算方法和探索手段、计算数据 计算电磁学与电磁场工程 电磁场工程为计算电磁学提供实验验证、需求牵引 计算电磁学为电磁场工程提供建模与仿真、优化与设计 近三十年来 电磁场理论的发展(探索未知) 电磁场工程的进步(需求牵引) 均与计算电磁学的发展密切相关

1.2电磁场问题求解方法分类 1966 @ 解析法、数值法、 半解析数值法 解析法 方程和求解 偏微分方程:泊松方程(静电场)、亥姆霍兹方程(时谐电磁场方程) 分离变量法 积分方程:电磁辐射/散射问题(积分核函数为格林函数) —变换数学法 >优点 √解为显式、可算出精确结果 √作为近似解和数值解的检验标准 √易于观察各参数对结果的影响和作用 > 缺点 不普适 例:标量亥姆霍兹方程只能在十一种坐标系下分离变量 11
11 1.2 电磁场问题求解方法分类 解析法、数值法、半解析数值法 解析法 方程和求解 偏微分方程:泊松方程(静电场)、亥姆霍兹方程(时谐电磁场方程) ——分离变量法 积分方程:电磁辐射/散射问题(积分核函数为格林函数)——变换数学法 优点 解为显式、可算出精确结果 作为近似解和数值解的检验标准 易于观察各参数对结果的影响和作用 缺点 不普适 例:标量亥姆霍兹方程只能在十一种坐标系下分离变量

1.2电磁场问题求解方法分类 966 近似解析法 ,根据所求解问题的解的范围 (定义域/值域) 该范围内成立的近似假设 简化模型、简化求解 √微扰法 √多极子展开近似 √高频近似法:几何光学近似、物理光学近似、几何绕射理论 √低频近似法:准静态近似 0●g● 现实问题干姿百态、近似假设层出不穷 新问题→新假设→新近似方法 12
12 1.2 电磁场问题求解方法分类 近似解析法 根据所求解问题的解的范围(定义域/值域) 该范围内成立的近似假设 简化模型、简化求解 微扰法 多极子展开近似 高频近似法 :几何光学近似、物理光学近似、几何绕射理论 低频近似法:准静态近似 …… 现实问题千姿百态、近似假设层出不穷 新问题 新假设 新近似方法
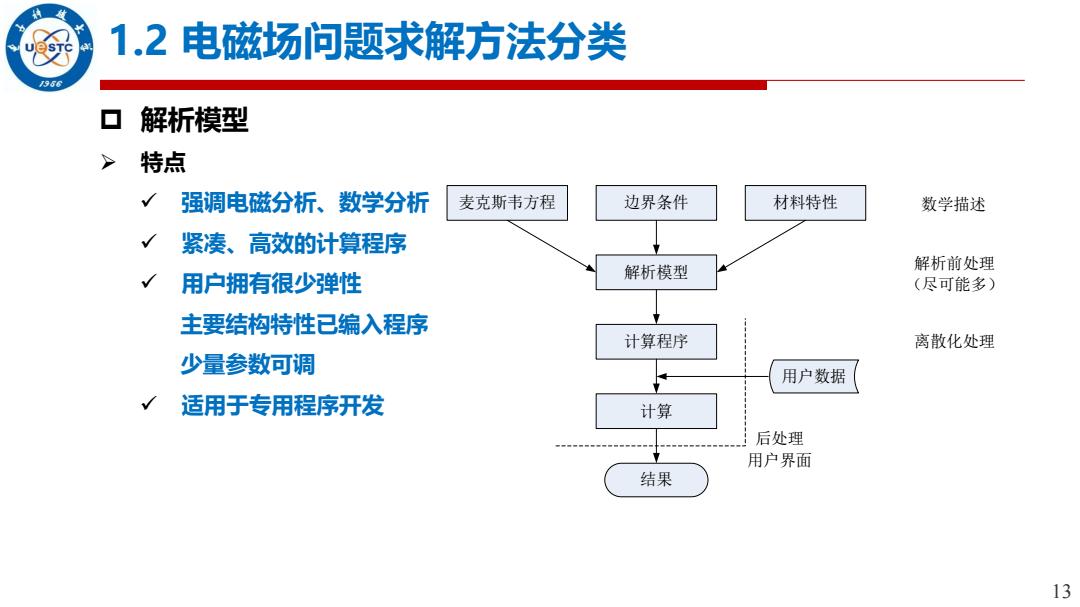
1.2电磁场问题求解方法分类 966 ▣ 解析模型 特点 强调电磁分析、数学分析 麦克斯韦方程 边界条件 材料特性 数学描述 紧凑、高效的计算程序 解析前处理 用户拥有很少弹性 解析模型 (尽可能多) 主要结构特性已编入程序 计算程序 离散化处理 少量参数可调 用户数据 适用于专用程序开发 计算 后处理 用户界面 结果 13
13 1.2 电磁场问题求解方法分类 解析模型 特点 强调电磁分析、数学分析 紧凑、高效的计算程序 用户拥有很少弹性 主要结构特性已编入程序 少量参数可调 适用于专用程序开发 麦克斯韦方程 边界条件 材料特性 解析模型 计算程序 计算 结果 用户数据 数学描述 解析前处理 (尽可能多) 离散化处理 后处理 用户界面