
M(T)=ng JugB,(y)…(I) 其中 B,y)=岁Coh2岁y-责Coh六…(2) 而 y=H kT =M(T)(3) J=1/2 J3/2 当T->0时,y一>∞,B(y)->1,代 0.8H J7/2 J=0 入(1)式M(T→0)=ngJ4g=M(0) 0.4 MT) M(0) =By)(4) 02 由(3)式两边同除, M(O)=ngJu得: M(T) kT M(0) na(gJua月 (5) 图2.19当J不同时的布里渊函数。 (4)式和(5)式都是以T为参数描述自发磁化强度,所 以相对值M(T)/M(O)随函数y变化的,前者为一曲线, 后者为一直线。当温度一定时,同时满足两式的解,就是
其中 而 当T->0时,y—> ∞,BJ(y)->1,代 入(1)式 M(T) ng J B (y)(1) J B J ( ) (2) 2 2 1 2 2 1 2 2 1 J y J J J J J BJ y Coth y Coth y H M (T)(3) k T Jg k T m JgJ B J B M (T 0) ng J M(0) J B ( ) (4) (0) ( ) B y M M T J 由(3)式两边同除 M (0) ngJ J B 得: 2 (5) ( ) (0) ( ) y J B n g J k T M M T (4)式和(5)式都是以T为参数描述自发磁化强度,所 以相对值M(T)/M(0)随函数y变化的,前者为一曲线, 后者为一直线。当温度一定时,同时满足两式的解,就是

所要求的M(T) M(T)/M(O) M(T)/M(O) H外0 H外≠0 1.0 J=1/2 A T=∞ 1.0 T/Tc 图解法求自发磁化强度 自发磁化强度随温度变化的曲线 2、随着温度的升高, (5)式的斜率逐渐增加,直至某一 温度时,直线的斜率与(4)式曲线的斜率在原点处相等, 此处自发磁化强度为零,此时的温度即为居里温度T。 T一>T.时,y<<1。由(4)式得 M(T) 3y(6) (J+1) M(0) (5),(6)式斜率相等可得出:
所要求的M(T)。 2、随着温度的升高,(5)式的斜率逐渐增加,直至某一 温度时,直线的斜率与(4)式曲线的斜率在原点处相等, 此处自发磁化强度为零,此时的温度即为居里温度Tc。 T-> Tc时,y<<1。由(4)式得 (5),(6)式斜率相等可得出:(6) 3 ( 1) (0) ( ) y J J M M T M(T)/M(0) 1 y A A’ 0 图解法求自发磁化强度 M(T)/M(0) T/TC 1.0 1.0 自发磁化强度随温度变化的曲线 J=1/2 J=∞ H外=0 H外≠0

+] nA(JgjHB) ng46J(J+1))2 3k 由此说明:T.随分子场系数入和总角动量量子数J的增大 而增大(只与物质的成分与晶体结构有关) 3.当温度超过居里点时,自发磁化消失,但每个原子仍是 有磁矩的。如加上外磁场, 则在磁场方向会有一总磁 矩M,设:M=ngJμB(y) 此时y中所包含的磁场是外磁场与分子场之和。(因为 考虑了原子磁矩之间的相互作用以后,只要物体内出 现总磁矩,便有一个分子场)即: JgjuB (H外十Hm)= JgjuB (H外十M)(8)
J J n Jg k T J B c 3 1 ( ) 2 (7) 3 ( 1) 2 2 k ng J J C J B T 由此说明:Tc随分子场系数λ和总角动量量子数J的增大 而增大(只与物质的成分与晶体结构有关)。 3.当温度超过居里点时,自发磁化消失,但每个原子仍是 有磁矩的。如加上外磁场,则在磁场方向会有一总磁 矩M’,设: M’ =ngJJμBB(y) 此时y中所包含的磁场是外磁场与分子场之和。(因为 考虑了原子磁矩之间的相互作用以后,只要物体内出 现总磁矩,便有一个分子场)即: ( ) ( )......(8) ' y H H k T H M Jg k T m JgJ B J B 外+ 外+

T>T。,则y<<1 .M=ngJ4B岁.(9) (⑧)式代入(9)式得: M = n(J+1)8a H外 3k T- n (J 3k 令 C nJ(J+1)g △= nJ(J+l)gjlBA 3k 3k =c 则 (10) (居里外斯定律) 1/x 其中△=Tc 实验发现,在居里点附近,沿直线外推 Tc 得到的与横轴的交点△,和实验曲线与 1/XT曲线 T 横轴的实际交点T有些差别,△称为顺磁居里点,/T称 为铁磁居里点
T>Tc,则y<<1 (8)式代入(9)式得: 令 则 (居里外斯定律) 其中 实验发现,在居里点附近,沿直线外推 得到的与 横轴的交点∆,和实验曲线与 横轴的实际交点TC有些差别, ∆称为顺磁居里点, TC称 为铁磁居里点。 .....(9) 3 ' 1 M ng J y J J J B [ ] 1 3 ( 1) 3 2 2 ( 1) 2 2 ' k J B nJ J g J B T k n J Jg H M 外 k nJ J gJ B C 3 ( 1) 2 2 c k nJ J gJ B 3 ( 1) 2 2 ........(10) T C TC 1/Χ 1/Χ~T曲线 T TC Δ
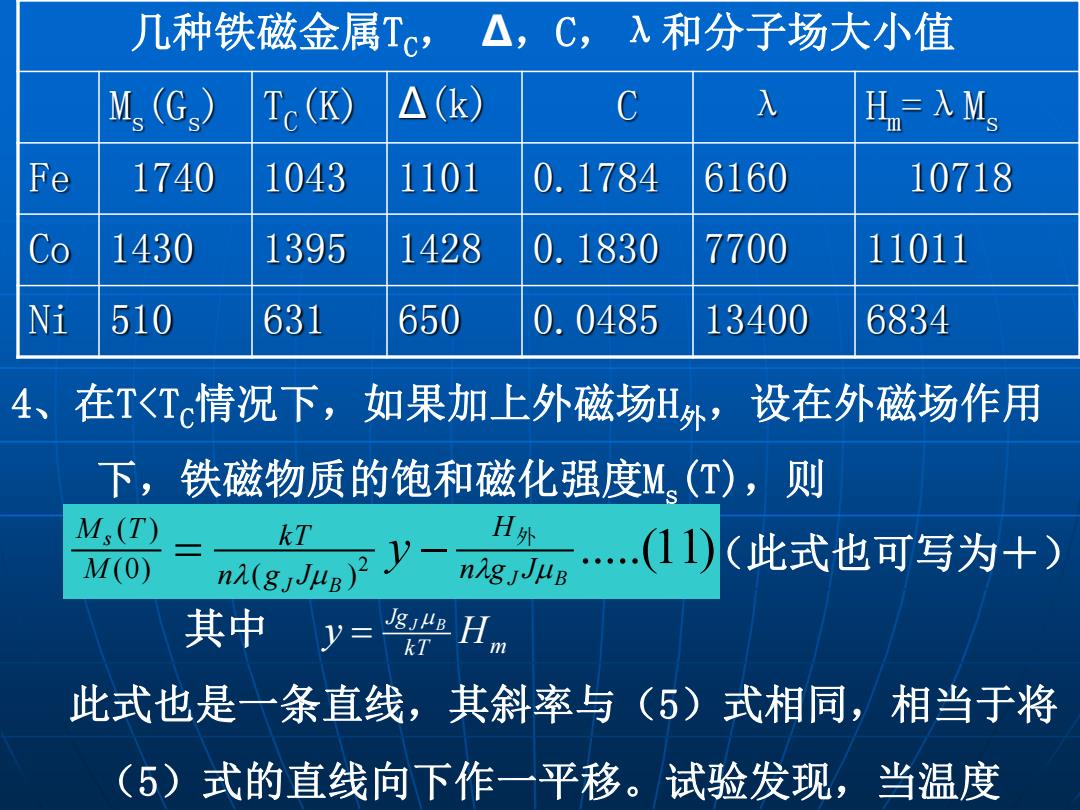
几种铁磁金属T,△,C,入和分子场大小值 M.(G) Tc(K) △(k) C 入 H=入4s Fe 1740 1043 1101 0.1784 6160 10718 Co 1430 1395 1428 0.1830 7700 11011 Ni 510 631 650 0.0485 13400 6834 4、在T<T情况下, 如果加上外磁场H外, 设在外磁场作用 下,铁磁物质的饱和磁化强度M、(T),则 M,(T) kT …(I山)(此式也可写为十) H处 M(0) n2(gJ4B)月 y-7 其中 JgjHB kT H 此式也是一条直线,其斜率与(5)式相同,相当于将 (5)式的直线向下作一平移。试验发现,当温度
几种铁磁金属TC, ∆,C,λ和分子场大小值 Ms(Gs) TC(K) ∆(k) C λ Hm=λMs Fe 1740 1043 1101 0.1784 6160 10718 Co 1430 1395 1428 0.1830 7700 11011 Ni 510 631 650 0.0485 13400 6834 4、在T<TC情况下,如果加上外磁场H外,设在外磁场作用 下,铁磁物质的饱和磁化强度Ms(T),则 (此式也可写为+) 其中 此式也是一条直线,其斜率与(5)式相同,相当于将 (5)式的直线向下作一平移。试验发现,当温度 2 .....(11) ( ) (0) ( ) J B J B s n g J H n g J k T M M T y 外 k T m Jg y J B H