海南大学：《电路原理》课程教学资源（课件讲稿）第十章 含有耦合电感的电路

例10-1：互感耦合电路中，求两耦合线圈中的磁通链 i1=10A,i2=5cos10t)A,L1=2H,L2=3H,M=1H ①2 N2 136 2 29 解 g=平1+乎12=L4+M=20+5cos(10t)W% Y平2=平21+平22=L2i2+M=10+15cos(10t)W%

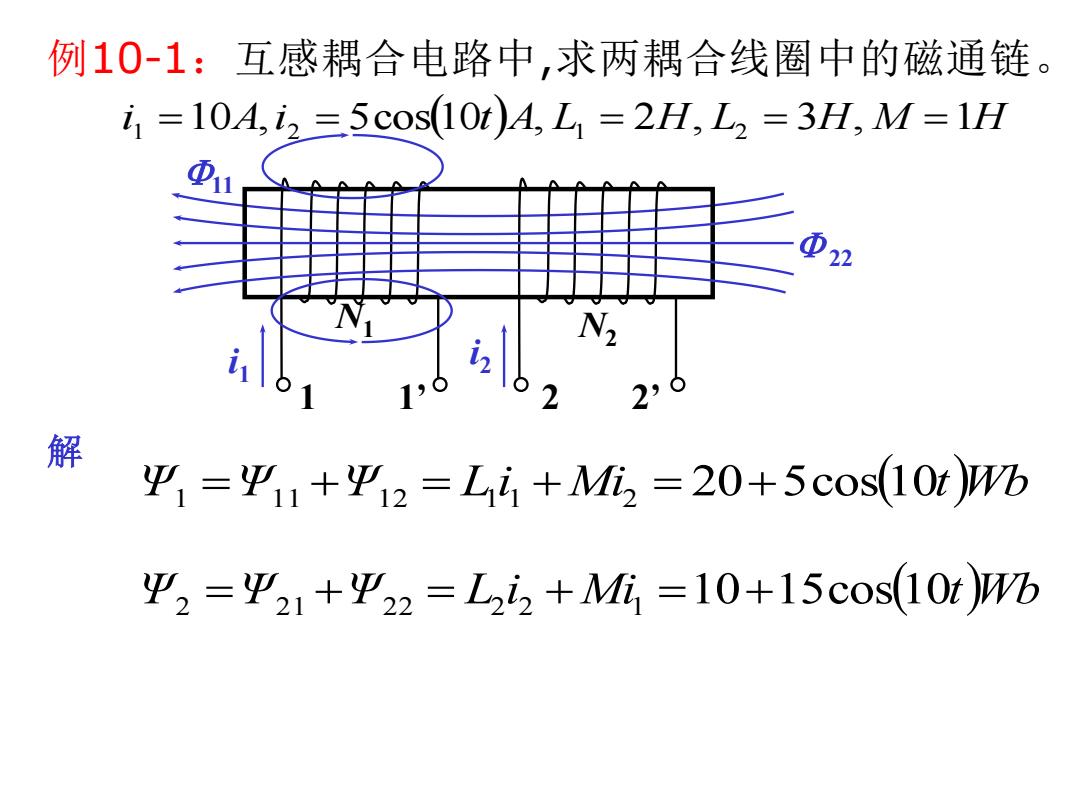
例10-1：互感耦合电路中,求两耦合线圈中的磁通链。 i 1 10A,i 2  5cos10tA, L1  2H, L2  3H, M 1H Ψ1 Ψ1 1 Ψ1 2  L1 i 1  Mi2  205cos10tWb Ψ2 Ψ2 1 Ψ2 2  L2 i 2  Mi1 1015cos10tWb 解 1 1’ 2 2’ i1 11  22 N1 N2 i2

例10-2：线圈的绕向及相互位置如下图，判断同名端 M前面为正 M前面为负

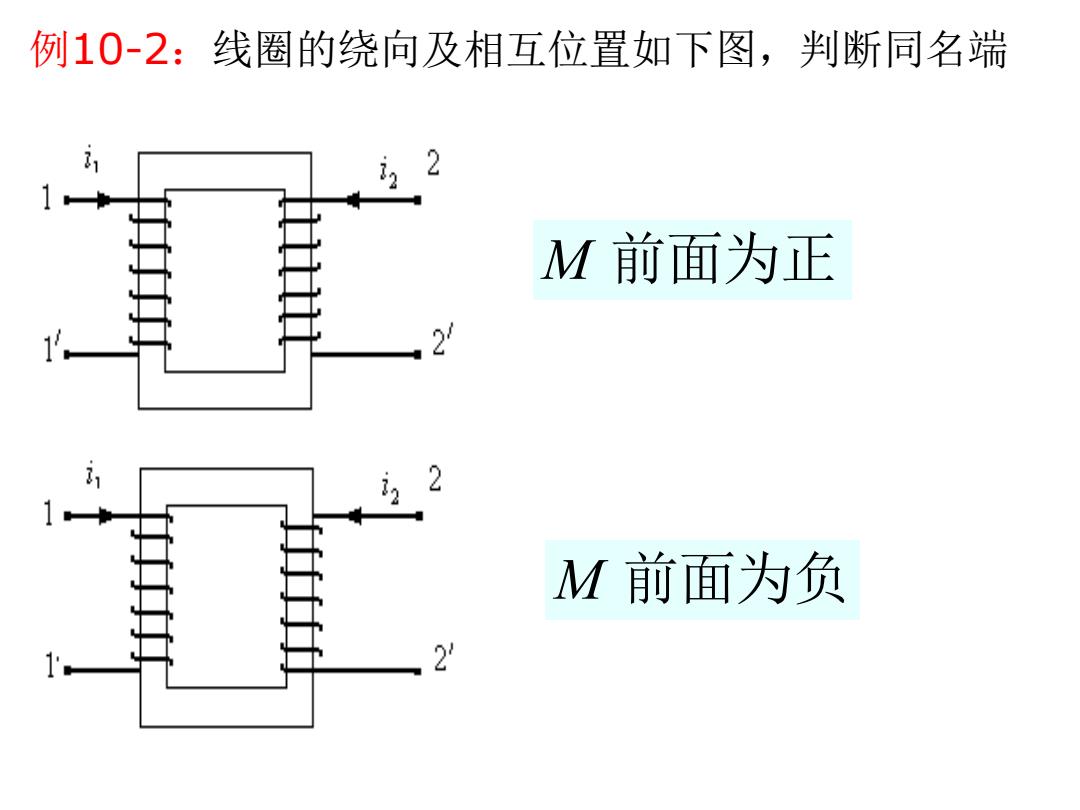
例10-2：线圈的绕向及相互位置如下图，判断同名端 M 前面为正 M 前面为负

三、耦合线圈中的感应电压 Ψ1=平1+Ψ2=L4±M122 Ψ2=Ψ2+Ψ21=L22±M2 N 自感电压 u uz u11= dΨu-L dt dt 1 三 d' ±M di dt dt dt 互感电压 M2= d2二L2 diz ±M di dt dt dt 42 dΨ2-M2 dt dt U1=joL,1±joM2i2 相量形式： U2=joL2I2±joM21i1

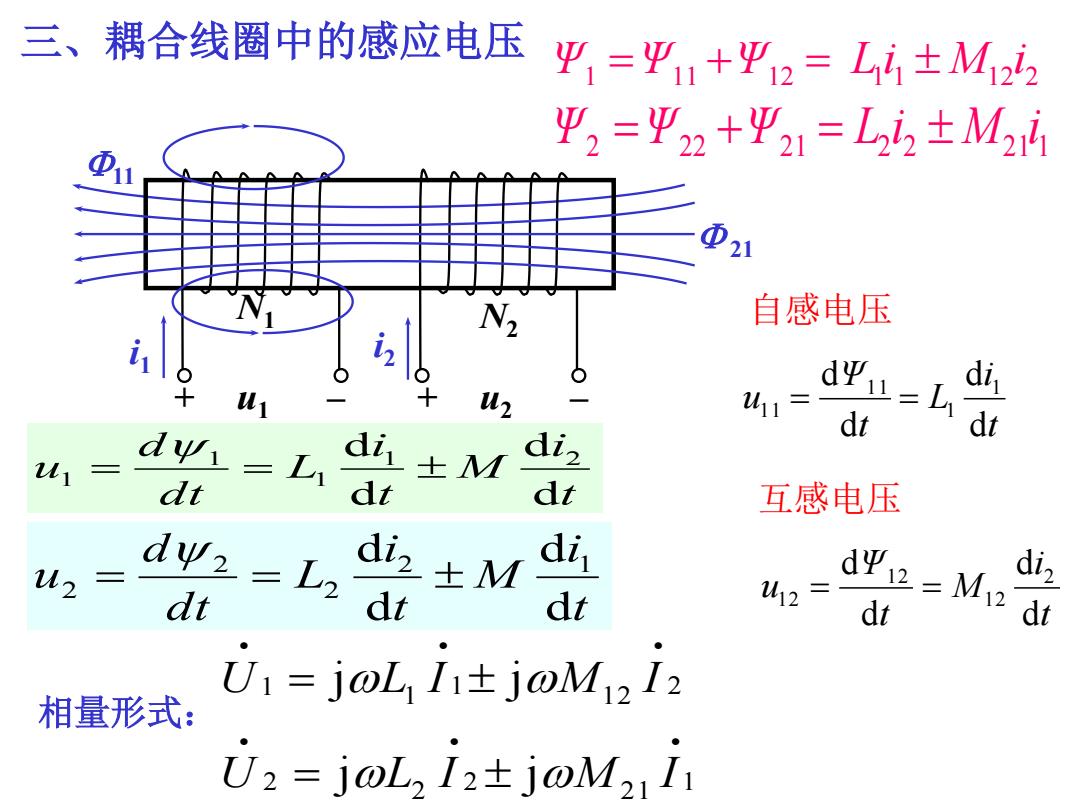
三、耦合线圈中的感应电压 1 11 12 1 1 12 2 Ψ Ψ Ψ  Li  M i 2 22 21 2 2 21 1 Ψ Ψ Ψ  L i  M i 1 2 1 2 2 2 2 1 2 1 1 1 j j j j           U L I M I U L I M I     t i M t i L dt d u d d d d 2 1 2 2 2     t i M t i L dt d u d d d d 1 2 1 1 1     相量形式： 自感电压 互感电压 t i L t Ψ u d d d d 1 1 1 1 1 1   t i M t Ψ u d d d d 2 1 2 1 2 1 2   + u1 – + u2 – i1 11  21 N1 N2 i2

例10-3：互感耦合电路中，求两耦合线圈的端电压。 i,=10A,i2=5cos10t)A,L1=2H,L2=3H,M=1H N2 解 u1=L1 di dt +M,=-50sin(10）y 互感电压 dt u2=L2 iz+M osam0y 自感电压

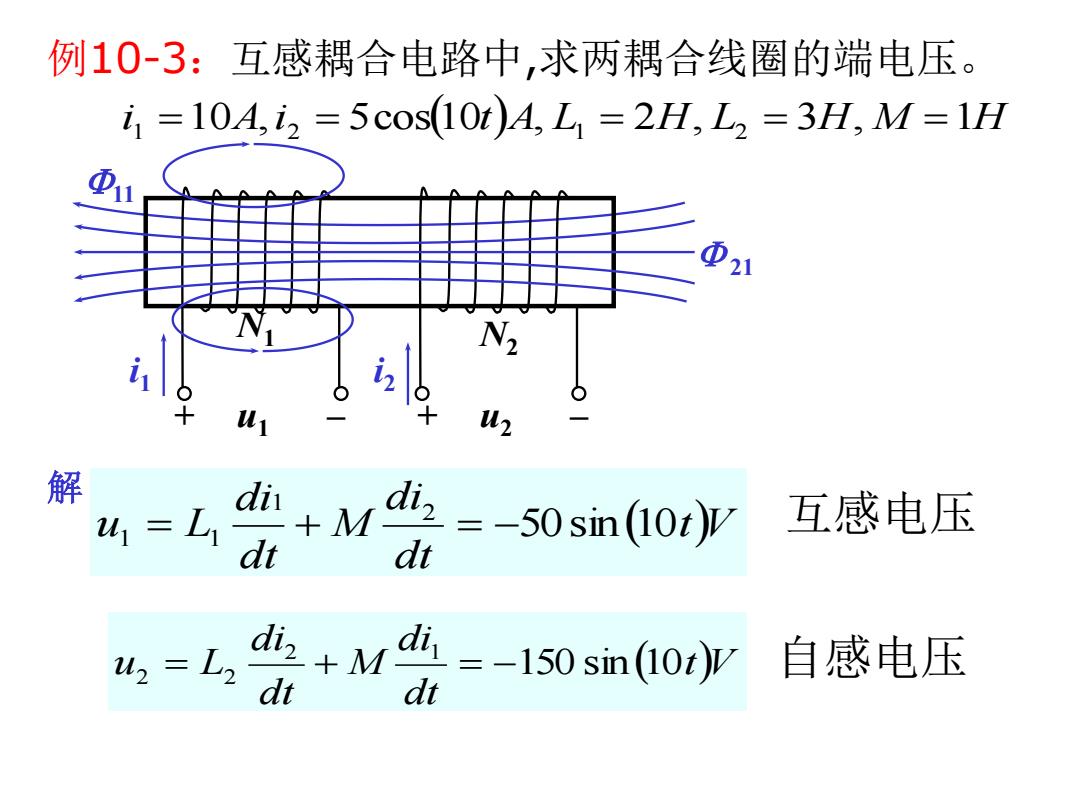
例10-3：互感耦合电路中,求两耦合线圈的端电压。 i 1 10A,i 2  5cos10tA, L1  2H, L2  3H, M 1H 解 + u1 – + u2 – i1 11  21 N1 N2  tV 互感电压 dt di M dt di u L 50sin 10 2 1 1  1     tV dt di M dt di u L 150 sin 10 2 1 2  2    自感电压 i2

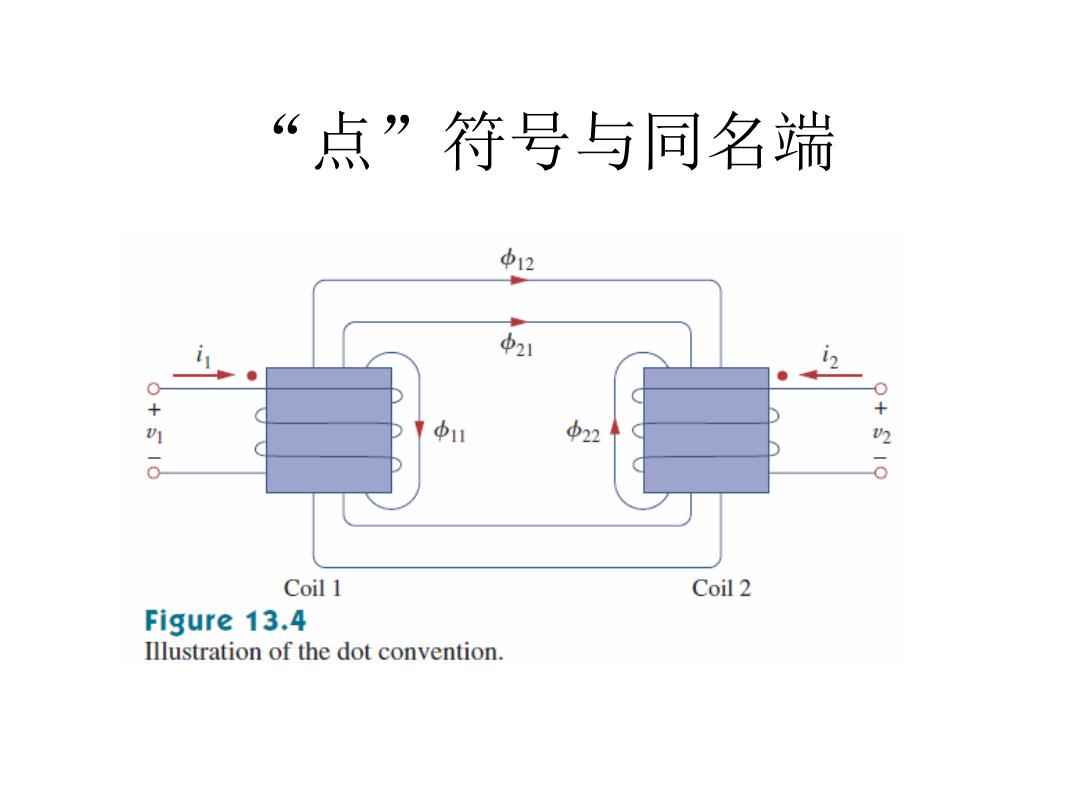
“点”符号与同名端 2 21 ● + + 中11 2 0 Coil 1 Coil 2 Figure 13.4 Illustration of the dot convention

“点”符号与同名端