
第二节 多元线性回归模型的估计 本节基本内容: ●普通最小二乘法(0LS) 0LS估计式的性质 0LS估计的分布性质 随机扰动项方差。的估计 回归系数的区间估计 16
16 第二节 多元线性回归模型的估计 本节基本内容: ● 普通最小二乘法(OLS) ● OLS估计式的性质 ● OLS估计的分布性质 ● 随机扰动项方差 的估计 ● 回归系数的区间估计 2 s

一、著通最小、二乘法(0LS) 最小二乘原则 剩余平方和最小:mm∑g=∑-穷 mim∑g=】y(月±β,x,+B,X,++X月 求偏导,令其为0: o1.0 a卵 17
17 一 、普通最小二乘法(OLS) 最小二乘原则 剩余平方和最小: 求偏导,令其为0: 2 2 m ˆ in ( - ) i i i å å e = Y Y 2 2 1 2 2 3 3 m ˆ ˆ ˆ ˆ in [ -( . )] i i i i k ki å å e = Y b +b X +b b X X + + 2 ( ) 0 ˆ b ¶ = ¶ å i j e

即 2(月+8x+8x+.+AX)0→∑9=0 2[Y(A+A±Ax+.+Ax)0→∑Xg=0 22Xy-(g+8x+0X+.±A)]0→∑Xae=0 注意到 y(±邛x±8x±.+AX幻9 18
18 即 注意到 1 2 2 3 3 ˆ ˆ ˆ ˆ é ù -(b +b +b b +. ) + = ë û Yi X i Xi kiX e ki i 0 i åe = 1 2 2 3 3 ˆ ˆ ˆ ˆ -2 é ù -(b +b +b b +.+ = ) 0 åë û Yi X i X X i ki ki 1 2 2 3 3 ˆ ˆ ˆ ˆ -2 é ù -(b +b +b b +.+ = ) 0 å ë û Xki Yi Xi X X i ki ki 2 1 2 2 3 3 ˆ ˆ ˆ ˆ -2 é ù -(b +b +b b +.+ = ) 0 å ë û X i Yi X i X X i ki ki 2 0 åX ei i = M M 0 åX eki i =
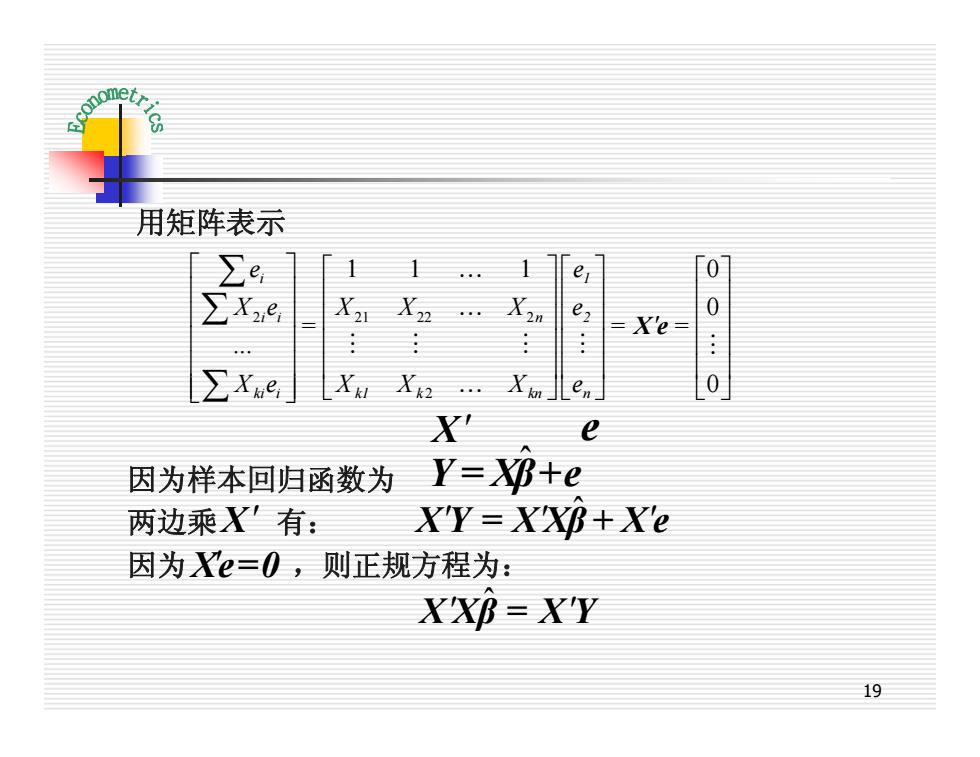
用矩阵表示 e 0 X X22 X2n 0 X'e ∑Xe 0 X e 因为样本回归函数为 Y=XB+e 两边乘X'有: XY=XXB+Ye 因为Xe=0,则正规方程为: XXB=XY 19
19 用矩阵表示 因为样本回归函数为 两边乘 有: 因为 ,则正规方程为: X¢ X¢e=0 2 21 22 2 2 1 1 1 0 0 0 i 1 i i n 2 ki i k1 k kn n e e X e X X X e = = = . X e X X X e é ù é ùé ù é ù ê ú ê úê ú ê ú ê ú ê úê ú ¢ ê ú ê ú ê úê ú ê ú ê ú ê úê ú ê ú ë û ê ú ë ûë û ë û å å å K K M M M M M K X e ˆ X X¢ ¢ β = X Y ˆ X¢Y = X X¢ ¢ β + X e Y = X ˆ β+e X¢ e

O儿S估计式 由正规方程X=XY(XX)x是满秩矩阵,其逆存在 多元回归中 B-CYYY 二元回归中 B=Y-0,x2月,x3 A2自-少公司 ∑x∑x)(∑)} A5-司 C∑x∑x)-(∑x,d 注意:X和y为XY的离差 20
20 由正规方程 多元回归中 二元回归中 注意: 和 为 的离差 ˆ ¢ ¢ -1 β=(XX) XY ( ) , k k ´ XX¢ ¢ β ˆ = XY X X¢ 是满秩矩阵 其逆存在 1 2 2 3 3 ˆ ˆ ˆ b = Y - β X - β X 2 3 2 2 2 3 3 2 2 2 2 3 2 3 ( )( ) -( )( ) ˆ ( )( ) -( ) i i i i i i i i i i i y x x y x x x x x x x b = å å å å å å å 2 2 3 3 2 3 2 2 2 2 2 3 2 3 ( )( )-( )( ) ˆ ( )( )-( ) i i i i i i i i i i i y x x y x x x x x x x b = å å å å å å å x y X,Y OLS估计式