
等容反应热与等压反应热的关系: 在等压或等容条件下,Qp≠Qv,反应热只取决于始态和终态,与变化的 途径无关。 Qv =△U Q,=△U+P△V Q,=QV+P△V 若反应体系内的反应物、产物全是固体或液体时,反应 过程中体积的变化很小,可以忽略。Q。≈Qv反应,若反 应中有气体参加,并假定所有的气体均为理想气体。则 Qp =Qy+△n(RT) △n为反应前后气态物质的物质的量之差
若反应体系内的反应物、产物全是固体或液体时,反应 过程中体积的变化很小,可以忽略。 Qp ≈QV反应,若反 应中有气体参加,并假定所有的气体均为理想气体。则 在等压或等容条件下, Qp ≠ QV ,反应热只取决于始态和终态,与变化的 途径无关。 等容反应热与等压反应热的关系: QV = ΔU Qp = ΔU + PΔV Qp = QV + PΔV Qp = QV + Δn(RT) Δn为反应前后气态物质的物质的量之差
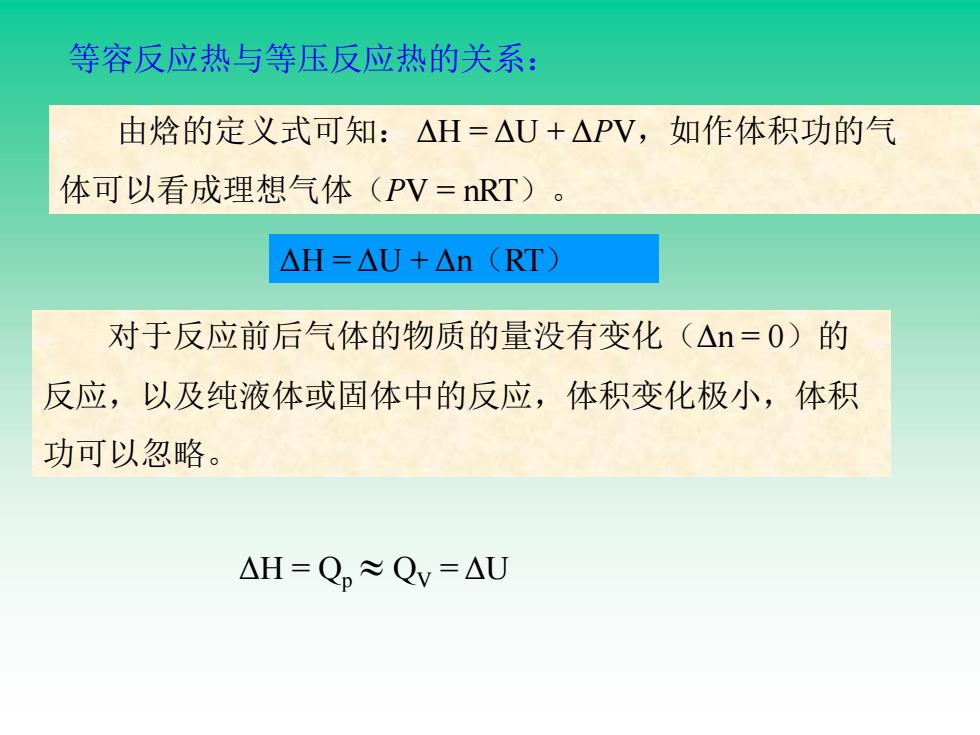
等容反应热与等压反应热的关系: 由焓的定义式可知:△H=△U+△PV,如作体积功的气 体可以看成理想气体(PV=nRT)。 △H=△U+△n(RT) 对于反应前后气体的物质的量没有变化(△n=0)的 反应,以及纯液体或固体中的反应,体积变化极小,体积 功可以忽略。 △H=Q,≈Qv=△U
对于反应前后气体的物质的量没有变化(Δn = 0)的 反应,以及纯液体或固体中的反应,体积变化极小,体积 功可以忽略。 ΔH = Qp QV = ΔU ΔH = ΔU + Δn(RT) 由焓的定义式可知: ΔH = ΔU + ΔPV,如作体积功的气 体可以看成理想气体(PV = nRT)。 等容反应热与等压反应热的关系:

[例2-2]已知298K时,反应 H2(g)+1/202(g)=H20(1) 的等压反应热为-285.8Kmo1。 求该条件下的等容反应热。 解:由公式Q,=Qv+△n(RT) 得 Qv=Qp-△n(RT) 由反应式可知△n=0-(1+1/2)=-1.5。 则 Qy=-285.8×103Jmo1-(-1.5) ×8.314JK-1mo1×298K =-282.1KJmo1
[例2-2] 已知298K时,反应 H2(g)+1/2O2(g)=H2O(l) 的等压反应热为-285.8KJ·mol-1 。 求该条件下的等容反应热。 解:由公式 Qp = QV + Δn(RT) 得 QV = Qp -Δn(RT) 由反应式可知Δn=0-(1+1/2)=-1.5。 则 QV = -285.8×103 J·mol-1-(-1.5) ×8.314J·K-1·mol-1×298K =-282.1KJ·mol-1

上述反应虽然体积变化较大,但△n(RT)的值 与Q或Q相比还是比较小的,对大多数反应来说, 若要求不十分严格,Qv和Q可认为近似相等。 对于化学的热效应可归纳如下: 1.焓(H)是一状态函数,定义式为H=U+PV 2.在等容过程中,不做其它功时,Qy=△U 3.在等压过程中,只有体积功时,Q=△H 4.对于理想气体反应,PV=nRT, Qp=Qy+△n(RT)
上述反应虽然体积变化较大,但Δn(RT)的值 与QV 或 QP 相比还是比较小的,对大多数反应来说, 若要求不十分严格, QV 和 QP可认为近似相等。 对于化学的热效应可归纳如下: 1.焓(H) 是一状态函数,定义式为H=U+PV 2.在等容过程中,不做其它功时,QV=ΔU 3.在等压过程中,只有体积功时,QP=ΔH 4.对于理想气体反应, PV = nRT, QP = QV + Δn(RT)

二、反应进度 对于任意的一个化学反应eE+fF=gG+hH 其中,e、不g、h为化学计量系数。 也可以表示为: 0=gG+hH-eE-fF 它也可用如下的通式表示: 0=Y,B 式中:B代表相应的反应物或产物;y为反应式中相应 物质B的化学计量数(stoichiometric number);∑表示反 应式中各物质求和。 对于反应物(reactant),vs为负值(如yE=-e,); 对于产物(product),y为正值(如vG=g,yHh)
也可以表示为: 0 = g G + h H – e E – f F 它也可用如下的通式表示: = B 0 B B 式中:B代表相应的反应物或产物;vB为反应式中相应 物质B的化学计量数(stoichiometric number); 表示反 应式中各物质求和。 B 对于反应物(reactant), vB为负值(如 vE = – e,); 对于产物(product),vB为正值(如vG = g, vH= h )。 二、反应进度 对于任意的一个化学反应 e E + f F = g G + h H 其中,e、f、g、h为化学计量系数