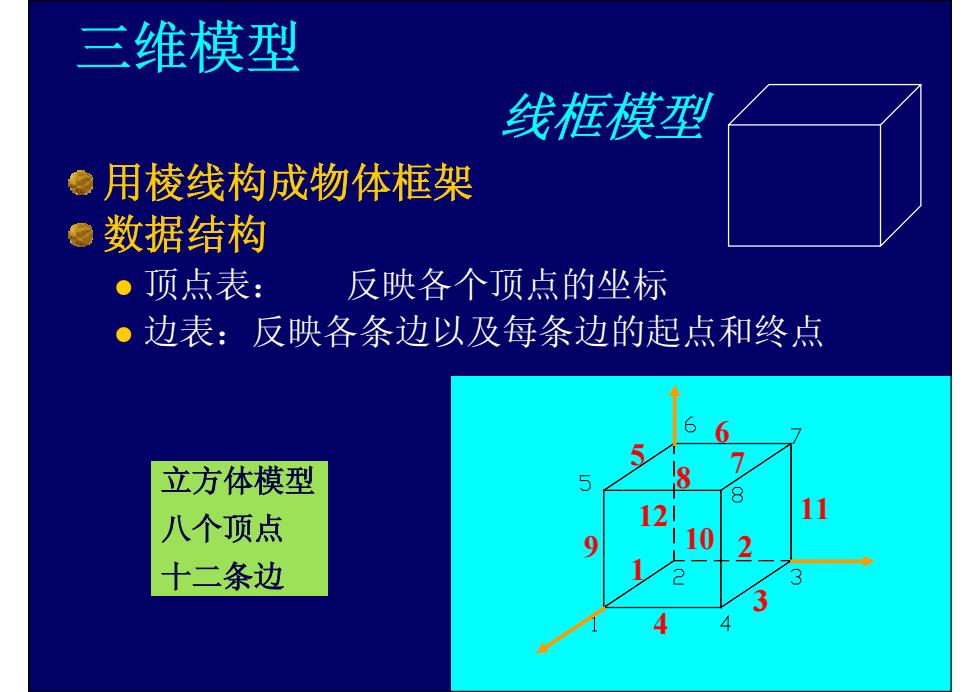
三维模型 线框模型 ●用棱线构成物体框架 ●数据结构 。顶点表: 反映各个顶点的坐标 ●边表:反映各条边以及每条边的起点和终点 6 6 5 7 立方体模型 5 8 八个顶点 12 11 110 2 十二条边 3 3 4
三维模型 线框模型 用棱线构成物体框架 数据结构 z 顶点表: 反映各个顶点的坐标 z 边表:反映各条边以及每条边的起点和终点 立方体模型 八个顶点 十二条边 4 3 1 2 5 6 7 8 9 10 12 11
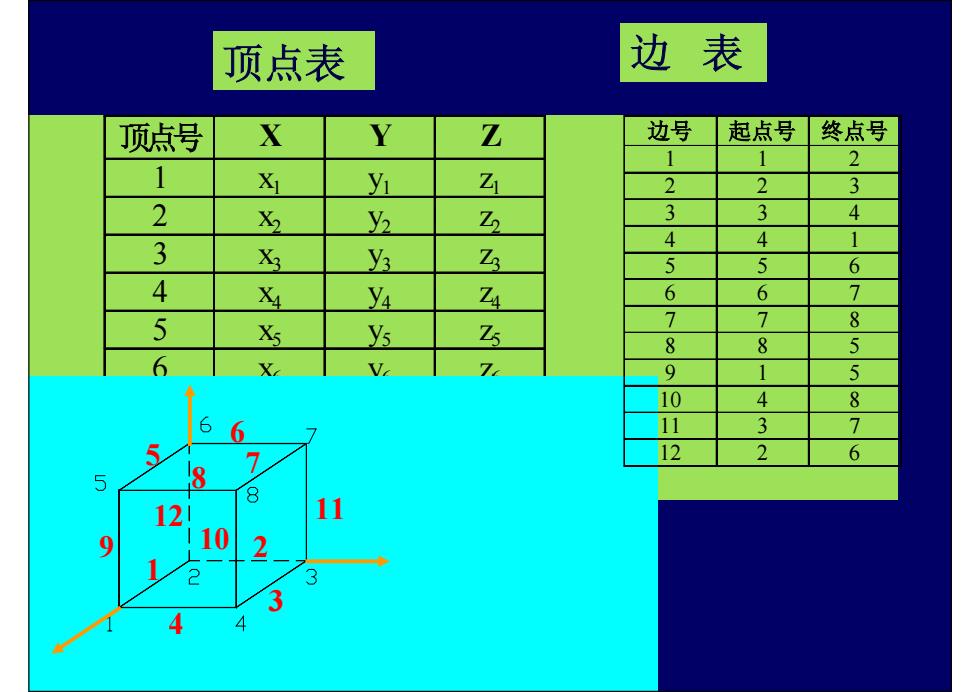
顶点表 边表 顶点号 X Y Z 边号 起点号 终点号 1 2 1 X y Z 2 2 3 2 X y2 Z 3 3 4 3 4 X 3 Z 5 5 6 4 X y4 Za 6 6 7 5 & 5 Z5 1 1 8 8 8 5 6 X V 7 9 1 5 10 4 8 6 11 3 7 5 7 12 2 6 5 8 12 11 9 10 3 3
顶点号 XYZ 1 x1 y1 z1 2 x2 y2 z2 3 x3 y3 z3 4 x4 y4 z4 5 x5 y5 z5 6 x6 y6 z6 7 x7 y7 z7 8 x8 y8 z8 顶点表 边 表 4 3 1 2 5 6 7 8 9 10 12 11 边号 起点号 终点号 112 223 334 441 556 667 778 885 915 10 4 8 11 3 7 12 2 6
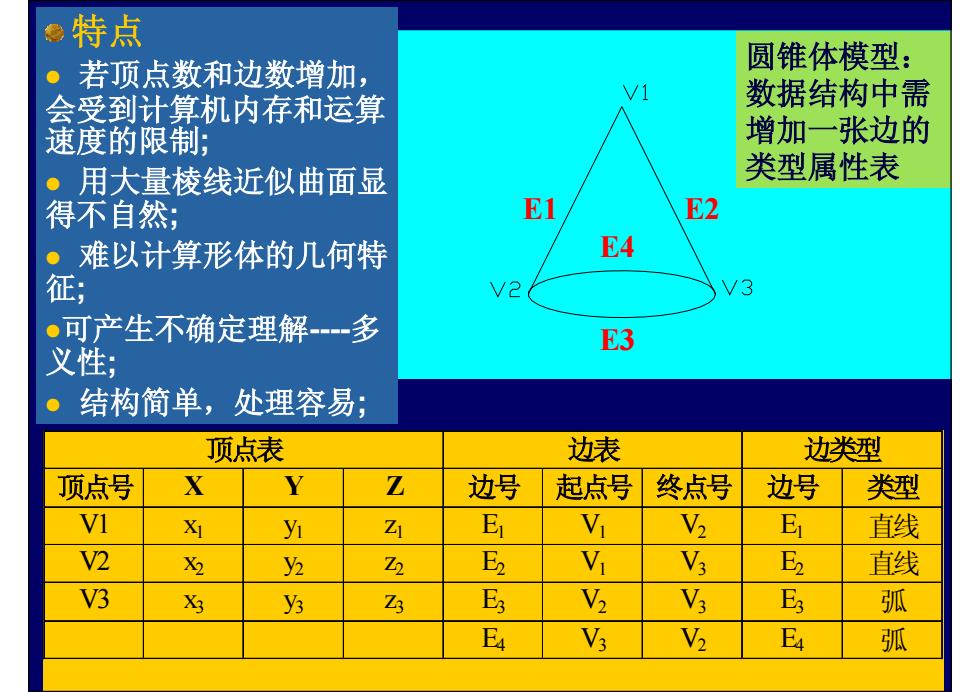
●特点 。若顶点数和边数增加, 圆锥体模型: 会受到计算机内存和运算 数据结构中需 速度的限制 增加一张边的 ●用大量棱线近似曲面显 类型属性表 得不自然; E1 E2 。难以计算形体的几何特 E4 征到 v2 V3 ●可产生不确定理解-多 E3 义性; 结构简单,处理容易; 顶点表 边表 边类型 顶点号 X Y Z 边号 起点号终点号 边号 类型 VI 为 y ☑ E V V32 E 直线 V2 X 2 Z2 E2 V V3 E 直线 V3 X Zs E V E 弧 Ea V3 V2 E 弧
E1 E2 E3 E4 圆锥体模型: 数据结构中需 增加一张边的 类型属性表 顶点表 边表 边类型 顶点号 X Y Z 边号 起点号 终点号 边号 类型 V1 x1 y1 z1 E1 V1 V2 E1 直线 V2 x2 y2 z2 E2 V1 V3 E2 直线 V3 x3 y3 z3 E3 V2 V3 E3 弧 E4 V3 V2 E4 弧 特点 z 若顶点数和边数增加, 会受到计算机内存和运算 速度的限制; z 用大量棱线近似曲面显 得不自然; z 难以计算形体的几何特 征; z可产生不确定理解-多 义性; z 结构简单,处理容易;
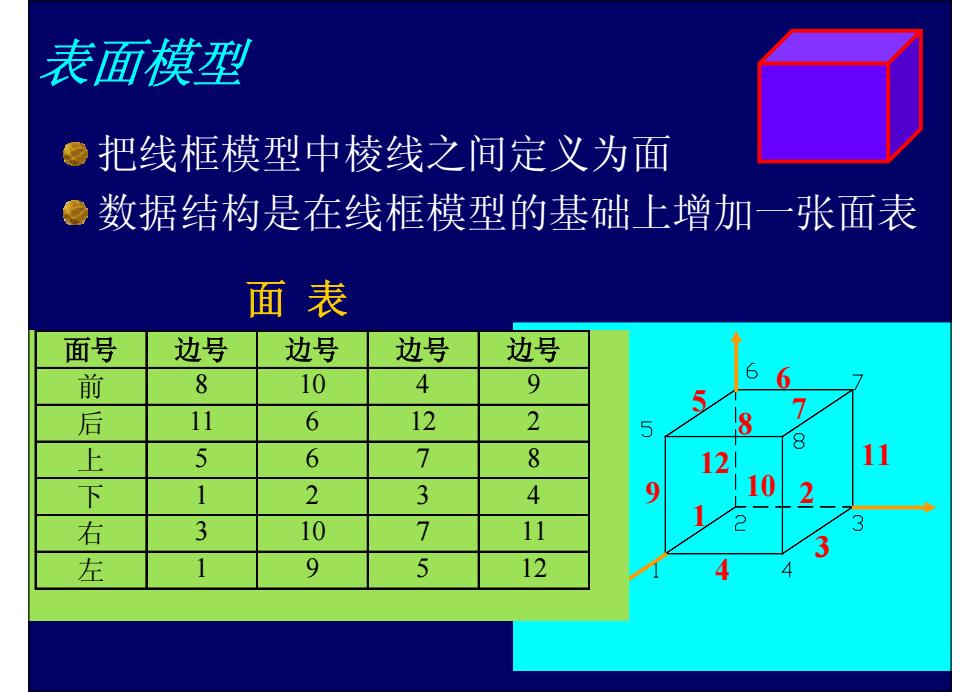
表面模型 ●把线框模型中棱线之间定义为面 ●数据结构是在线框模型的基础上增加一张面表 面表 面号 边号 边号 边号 边号 前 8 10 4 9 后 11 6 12 2 5 8 7 8 上 5 6 7 8 12 11 下 2 3 4 9 10 2 右 3 10 1 11 2 3 3 左 1 9 5 12
4 3 1 2 5 6 7 8 9 10 12 11 表面模型 把线框模型中棱线之间定义为面 数据结构是在线框模型的基础上增加一张面表 面号 边号 边号 边号 边号 前 8 10 4 9 后 11 6 12 2 上 5678 下 1234 右 3 10 7 11 左 1 9 5 12 面 表

特点 ●对线框模型的多义性有所改善 ·形体边界可以全部定义 。可生成剖面图和进行消隐处理 ·缺乏表示形体内部结构的能力 ·对于三维实体还具有某些多义性
特点 z 对线框模型的多义性有所改善 z 形体边界可以全部定义 z 可生成剖面图和进行消隐处理 z 缺乏表示形体内部结构的能力 z 对于三维实体还具有某些多义性