
这样,独立的宏观对称元素便只有1,2,3,4,4,6,i,m,将这些对称元素按群的规则 组合起来,便得到32种晶类。因为进行对称操作时,这些对称元素必至少相交于一点,即 物体中至少有一点在变换中保持不动.所以32晶类又称32点群。许多资料都把32点群表 列了出来。望读者容略。 2.晶体的微观对称(含平移的对称) 当深入到晶体的微观尺度考察其对称性时,就可发现晶体的原子排列除具有如上所 述的宏观对称性,还具有平移对称性以及反映面+平移对称性、旋转+平移的对称性。 (1)平移。把空间点阵的阵点所代表的原子沿某方向移动该方向的一个周期,整个结 构不变,即称其具有平移对称性。空间点阵的无限延伸特性保证了平移对称操作的实施。 ②)滑移面。结构中一原子经反映面反映后,再沿平行于反映面的某方向平移或该方 向的一个周期T,或亏、或周期使结构复原。依据平移方向是晶胞的a、b、c或a+b等, 分别标以a(号)、b()c(号)、da主)、nab)等,这里括号()中的内容是平 移量,也称“滑移量”。 3)螺旋轴。原子经旋转移动到一位置后,再沿旋转轴方向平移工·1至等同原子的 位置。这里n=2,3,4,6,1=1,2…(n-1)。螺旋轴的符号有21,31,32…和0▲ …。这里 所述的对称操作都是对微观位置的原子(或其集合)施行的。因此称这几种对称为晶体的 微观对称。图2.4a)b)表示了两种微观对称操作。 螺旋轴 遵龄移面 图2.4螺旋轴和滑移面 把各种宏观对称操作及微观对称操作按群的规则组合起来,得到230种群,称为空间 群。它是描述晶体结构的重要工具。至今所发现的晶体结构还没有不可用空间群描述的。 表2.1列举了晶体中可能存在的对称元素及其表示符号。 ·25·
这样,独立的宏观对称元素便只有1,2,3,4,4,6,i,m,将这些对称元素按群的规则 组合起来,便得到32种晶类。因为进行对称操作时,这些对称元素必至少相交于一点,即 物体中至少有一点在变换中保持不动。所以32晶类又称32点群。许多资料都把32点群表 列了出来。望读者容略。 2.晶体的微观对称(含平移的对称) 当深入到晶体的微观尺度考察其对称性时,就可发现晶体的原子排列除具有如上所 述的宏观对称性,还具有平移对称性以及反映面 +平移对称性、旋转+平移的对称性。 (1)平移。把空间点阵的阵点所代表的原子沿某方向移动该方向的一个周期,整个结 构不变,即称其具有平移对称性。空间点阵的无限延伸特性保证了平移对称操作的实施。 (2)滑移面。结构中一原子经反映面反映后,再沿平行于反映面的某方向平移或该方 向的一个周期T,或1 2、或1 4 周期使结构复原。依据平移方向是晶胞的a、b、c或a+b等, 分别标以a(a 2)、b(b 2)、c(c 2)、d(a±b 4 )、n(a±b 2 )等,这里括号( )中的内容是平 移量,也称“滑移量”。 (3)螺旋轴。原子经旋转移动到一位置后,再沿旋转轴方向平移T n·l至等同原子的 位置。这里n =2,3,4,6,l=1,2…(n-1)。螺旋轴的符号有21,31,32… 和 …。这里 所述的对称操作都是对微观位置的原子(或其集合)施行的。因此称这几种对称为晶体的 微观对称。图24(a)(b)表示了两种微观对称操作。 穴葬雪源员螺旋轴 穴遭雪葬滑移面 员辕源栽 栽 葬辕圆 图24 螺旋轴和滑移面 把各种宏观对称操作及微观对称操作按群的规则组合起来,得到230种群,称为空间 群。它是描述晶体结构的重要工具。至今所发现的晶体结构还没有不可用空间群描述的。 表21列举了晶体中可能存在的对称元素及其表示符号。 · 52 ·
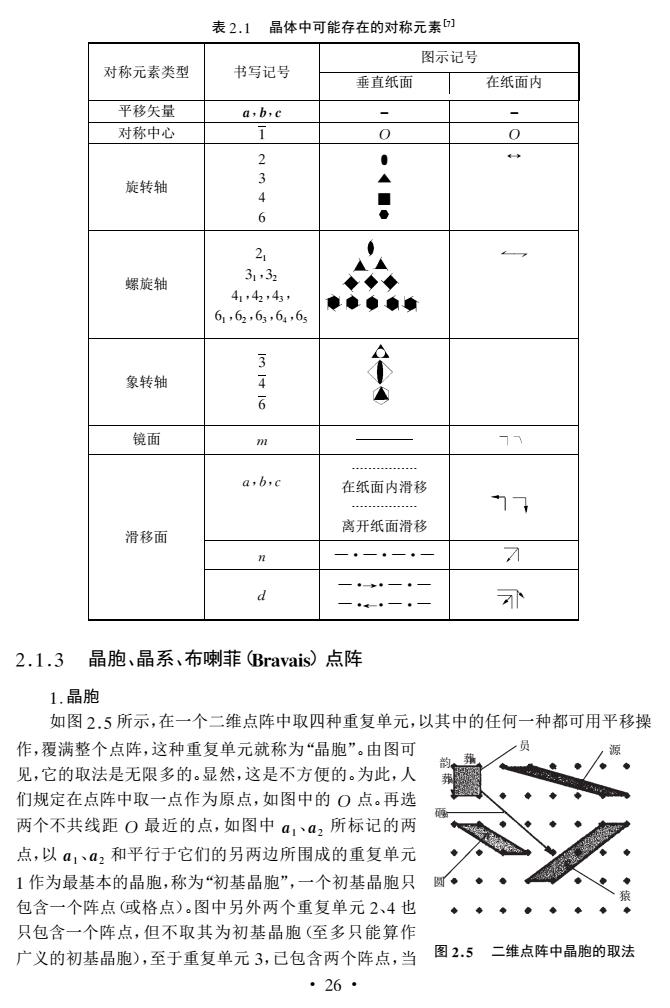
表2.1晶体中可能存在的对称元素 图示记号 对称元素类型 书写记号 垂直纸面 在纸面内 平移矢量 a,b,c 对称中心 0 0 2 3 旋转轴 6 螺旋轴 31,32 ◆◆◆ 41,4,4 电◆◆ 61,62,63,6,6 象转轴 46 镜面 a,b,c 在纸面内滑移 77 离开纸面滑移 滑移面 n 7 2.1.3晶胞、晶系,布喇菲Bravais)点阵 1.晶胞 如图2.5所示,在一个二维点阵中取四种重复单元,以其中的任何一种都可用平移操 作,覆满整个点阵,这种重复单元就称为“晶胞”。由图可 见,它的取法是无限多的。显然,这是不方便的。为此,人 们规定在点阵中取一点作为原点,如图中的O点。再选 两个不共线距0最近的点,如图中a1a2所标记的两 点,以a1、a2和平行于它们的另两边所围成的重复单元 1作为最基本的晶胞,称为“初基晶胞”,一个初基晶胞只 包含一个阵点(或格点)。图中另外两个重复单元2、4也 只包含一个阵点,但不取其为初基晶胞(至多只能算作 广义的初基晶胞),至于重复单元3,己包含两个阵点,当 图2.5二维点阵中晶胞的取法 ·26·
表21 晶体中可能存在的对称元素[7] 对称元素类型 书写记号 图示记号 垂直纸面 在纸面内 平移矢量 a,b,c - - 对称中心 1 O O 旋转轴 2 3 4 6 ▲ ■ 螺旋轴 21 31,32 41,42,43, 61,62,63,64,65 象转轴 3 4 6 镜面 m 滑移面 a,b, c 在纸面内滑移 离开纸面滑移 n —·—·—·— d —·→·—·— —·←·—·— 葬圆 葬员 韵 猿 员 源 砸员 圆 图25 二维点阵中晶胞的取法 213 晶胞、晶系、布喇菲(Bravais)点阵 1.晶胞 如图25所示,在一个二维点阵中取四种重复单元,以其中的任何一种都可用平移操 作,覆满整个点阵,这种重复单元就称为“晶胞”。由图可 见,它的取法是无限多的。显然,这是不方便的。为此,人 们规定在点阵中取一点作为原点,如图中的 O 点。再选 两个不共线距 O 最近的点,如图中a1、a2 所标记的两 点,以a1、a2 和平行于它们的另两边所围成的重复单元 1作为最基本的晶胞,称为“初基晶胞”,一个初基晶胞只 包含一个阵点(或格点)。图中另外两个重复单元2、4也 只包含一个阵点,但不取其为初基晶胞(至多只能算作 广义的初基晶胞),至于重复单元3,已包含两个阵点,当 · 62 ·
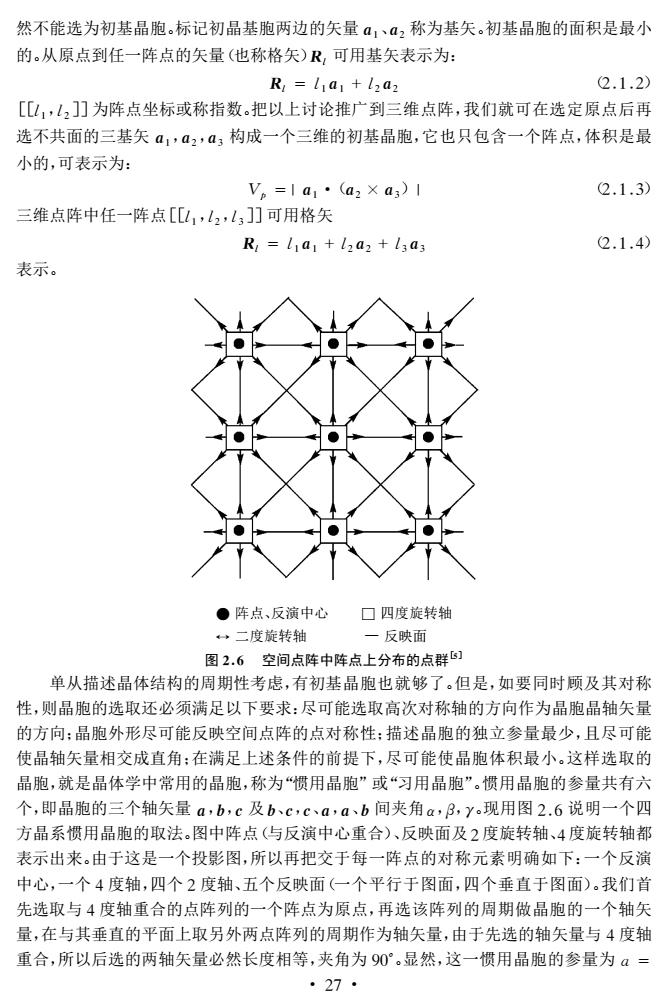
然不能选为初基晶胞。标记初品基胞两边的矢量a1、a2称为基矢。初基晶胞的面积是最小 的。从原点到任一阵点的矢量(也称格矢)R,可用基矢表示为: Ry=lia+lzaz 2.1.2) [山,L2]为阵点坐标或称指数。把以上讨论推广到三维点阵,我们就可在选定原点后再 选不共面的三基矢a1,a2,a3构成一个三维的初基晶胞,它也只包含一个阵点,体积是最 小的,可表示为: V。=1a1·(a2Xa3)I 2.1.3) 三维点阵中任一阵点[山1,l2,l3]可用格矢 Ri=lia+lzaz+l3a; 2.1.4) 表示。 ●阵点、反演中心口四度旋转轴 二度旋转轴 一反映面 图2.6空间点阵中阵点上分布的点群 单从描述晶体结构的周期性考虑,有初基晶胞也就够了。但是,如要同时顾及其对称 性,则晶胞的选取还必须满足以下要求:尽可能选取高次对称轴的方向作为晶胞晶轴矢量 的方向:晶胞外形尽可能反映空间点阵的点对称性:描述晶胞的独立参量最少,且尽可能 使晶轴矢量相交成直角:在满足上述条件的前提下,尽可能使晶胞体积最小。这样选取的 晶胞,就是晶体学中常用的晶胞,称为“惯用品胞”或“习用晶胞”。惯用晶胞的参量共有六 个,即晶胞的三个轴矢量a,b,c及b、c,c、a,a、b间夹角a,B,y。现用图2.6说明一个四 方晶系惯用晶胞的取法。图中阵点(与反演中心重合)、反映面及2度旋转轴、4度旋转轴都 表示出来。由于这是一个投影图,所以再把交于每一阵点的对称元素明确如下:一个反演 中心,一个4度轴,四个2度轴、五个反映面(一个平行于图面,四个垂直于图面).我们首 先选取与4度轴重合的点阵列的一个阵点为原点,再选该阵列的周期做晶胞的一个轴矢 量,在与其垂直的平面上取另外两点阵列的周期作为轴矢量,由于先选的轴矢量与4度轴 重合,所以后选的两轴矢量必然长度相等,夹角为90°。显然,这一惯用晶胞的参量为a= ·27
然不能选为初基晶胞。标记初晶基胞两边的矢量a1、a2称为基矢。初基晶胞的面积是最小 的。从原点到任一阵点的矢量(也称格矢)Rl 可用基矢表示为: Rl =l1a1 +l2a2 (212) [[l1,l2]]为阵点坐标或称指数。把以上讨论推广到三维点阵,我们就可在选定原点后再 选不共面的三基矢a1,a2,a3 构成一个三维的初基晶胞,它也只包含一个阵点,体积是最 小的,可表示为: Vp =|a1·(a2 ×a3)| (213) 三维点阵中任一阵点[[l1,l2,l3]]可用格矢 Rl =l1a1 +l2a2 +l3a3 (214) 表示。 ● 阵点、反演中心 □ 四度旋转轴 二度旋转轴 — 反映面 图26 空间点阵中阵点上分布的点群[5] 单从描述晶体结构的周期性考虑,有初基晶胞也就够了。但是,如要同时顾及其对称 性,则晶胞的选取还必须满足以下要求:尽可能选取高次对称轴的方向作为晶胞晶轴矢量 的方向;晶胞外形尽可能反映空间点阵的点对称性;描述晶胞的独立参量最少,且尽可能 使晶轴矢量相交成直角;在满足上述条件的前提下,尽可能使晶胞体积最小。这样选取的 晶胞,就是晶体学中常用的晶胞,称为“惯用晶胞”或“习用晶胞”。惯用晶胞的参量共有六 个,即晶胞的三个轴矢量a,b,c及b、c,c、a,a、b间夹角α,β,γ。现用图26说明一个四 方晶系惯用晶胞的取法。图中阵点(与反演中心重合)、反映面及2度旋转轴、4度旋转轴都 表示出来。由于这是一个投影图,所以再把交于每一阵点的对称元素明确如下:一个反演 中心,一个4度轴,四个2度轴、五个反映面(一个平行于图面,四个垂直于图面)。我们首 先选取与4度轴重合的点阵列的一个阵点为原点,再选该阵列的周期做晶胞的一个轴矢 量,在与其垂直的平面上取另外两点阵列的周期作为轴矢量,由于先选的轴矢量与4度轴 重合,所以后选的两轴矢量必然长度相等,夹角为90°。显然,这一惯用晶胞的参量为a = · 72 ·
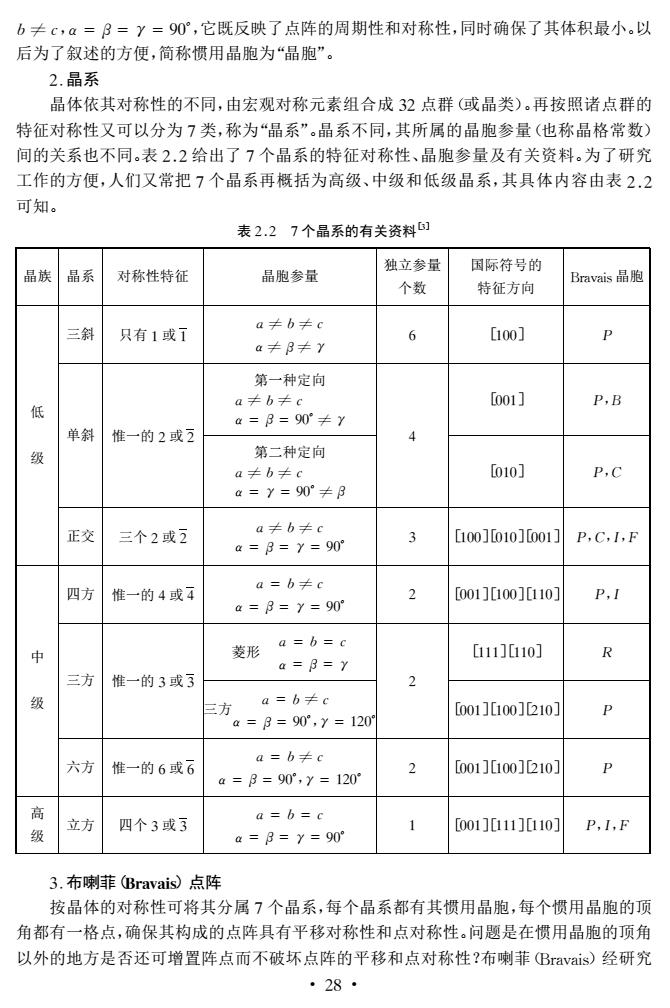
b≠c,a=B=y=90°,它既反映了点阵的周期性和对称性,同时确保了其体积最小。以 后为了叙述的方便,简称惯用晶胞为“品胞”。 2.晶系 晶体依其对称性的不同,由宏观对称元素组合成32点群(或晶类)。再按照诸点群的 特征对称性又可以分为7类,称为“晶系”。晶系不同,其所属的晶胞参量(也称晶格常数) 间的关系也不同。表2.2给出了7个晶系的特征对称性、晶胞参量及有关资料。为了研究 工作的方便,人们又常把7个晶系再概括为高级、中级和低级晶品系,其具体内容由表2.2 可知。 表2.27个晶系的有关资料6 晶族晶系 对称性特征 晶胞参量 独立参量 国际符号的 Bravais晶胞 个数 特征方向 三斜 只有1或了 a≠b≠ 100] P a≠B≠y 6 第一种定向 a≠b≠。 001] 低 P,B a=B=90≠y 单斜 惟一的2或2 4 第二种定向 a≠b≠c 010] P,C a=Y=90°≠B 正交 a≠b≠c 三个2或2 10m0101f001 a=B=y=90 P,C,I,F 四方惟一的4或4 a=b≠c [001]000]010] P,I a=3=y=90 中 011]010] R a=3=Y 三方惟一的3或3 2 级 a=b≠c 三 a=B=90,y=120 [001]100]210] P a=b≠c 六方惟一的6或6 2 [001]0100]210] a=B=90°,Y=120 高 立方 四个3或3 a=b=c [001]011]0110] P,1,F 级 a==Y=90 3.布喇菲(Bravais)点阵 按晶体的对称性可将其分属7个晶系,每个晶系都有其惯用晶胞,每个惯用晶胞的顶 角都有一格点,确保其构成的点阵具有平移对称性和点对称性。问题是在惯用晶胞的顶角 以外的地方是否还可增置阵点而不破坏点阵的平移和点对称性?布喇菲Bravais)经研究 ·28·
b≠c,α=β=γ=90°,它既反映了点阵的周期性和对称性,同时确保了其体积最小。以 后为了叙述的方便,简称惯用晶胞为“晶胞”。 2.晶系 晶体依其对称性的不同,由宏观对称元素组合成32点群(或晶类)。再按照诸点群的 特征对称性又可以分为7类,称为“晶系”。晶系不同,其所属的晶胞参量(也称晶格常数) 间的关系也不同。表22给出了7个晶系的特征对称性、晶胞参量及有关资料。为了研究 工作的方便,人们又常把7个晶系再概括为高级、中级和低级晶系,其具体内容由表22 可知。 表22 7个晶系的有关资料[3] 晶族 晶系 对称性特征 晶胞参量 独立参量 个数 国际符号的 特征方向 Bravais晶胞 低 级 三斜 只有1或1 a≠b≠c α≠β≠γ 6 [100] P 单斜 惟一的2或2 第一种定向 a≠b≠c α=β=90°≠γ 第二种定向 a≠b≠c α=γ=90°≠β 4 [001] P,B [010] P,C 正交 三个2或2 a≠b≠c α=β=γ=90° 3 [100][010][001] P,C,I,F 中 级 四方 惟一的4或4 a=b≠c α=β=γ=90° 2 [001][100][110] P,I 三方 惟一的3或3 菱形 a=b=c α=β=γ 三方 a=b≠c α=β=90°,γ=120° 2 [111][110] R [001][100][210] P 六方 惟一的6或6 a=b≠c α=β=90°,γ=120° 2 [001][100][210] P 高 级 立方 四个3或3 a=b=c α=β=γ=90° 1 [001][111][110] P,I,F 3.布喇菲(Bravais)点阵 按晶体的对称性可将其分属7个晶系,每个晶系都有其惯用晶胞,每个惯用晶胞的顶 角都有一格点,确保其构成的点阵具有平移对称性和点对称性。问题是在惯用晶胞的顶角 以外的地方是否还可增置阵点而不破坏点阵的平移和点对称性?布喇菲(Bravais)经研究 · 82 ·
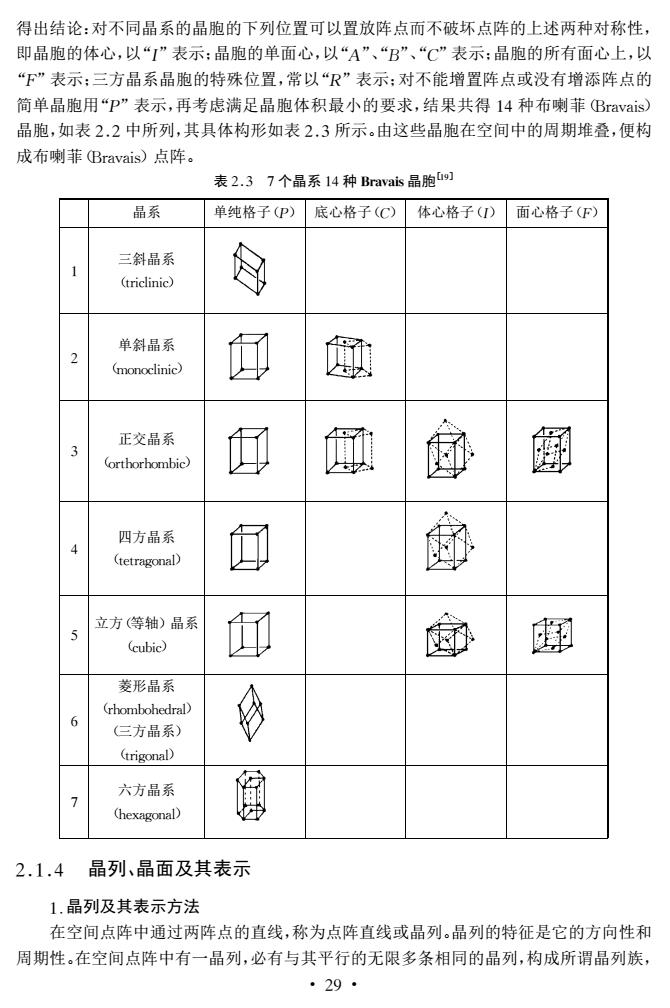
得出结论:对不同晶系的品胞的下列位置可以置放阵点而不破坏点阵的上述两种对称性, 即晶胞的体心,以“I”表示:晶胞的单面心,以“A”、“B”、“C”表示:晶胞的所有面心上,以 “F”表示:三方晶系晶胞的特殊位置,常以“R”表示:对不能增置阵点或没有增添阵点的 简单晶胞用“P”表示,再考虑满足晶胞体积最小的要求,结果共得14种布喇菲(Bravais). 晶胞,如表2.2中所列,其具体构形如表2.3所示。由这些晶胞在空间中的周期堆叠,便构 成布喇菲Bravais)点阵。 表2.37个晶系14种Bnak晶胞9 晶系 单纯格子P) 底心格子(C) 体心格子()面心格子(F) 三斜晶系 单斜晶系 (monoclinic) 正交晶系 每 @ 四方晶系 (tetragonal) 立方(等轴)晶系 (cubic) 厨 觑 菱形品系 (rhombohedral) 6 三方晶系) (trigonal) 六方晶系 7 (hexagonal) 2.1.4晶列、晶面及其表示 1.晶列及其表示方法 在空间点阵中通过两阵点的直线,称为点阵直线或品列。品列的特征是它的方向性和 周期性。在空间点阵中有一晶列,必有与其平行的无限多条相同的晶列,构成所谓晶列族 ·29
得出结论:对不同晶系的晶胞的下列位置可以置放阵点而不破坏点阵的上述两种对称性, 即晶胞的体心,以“I”表示;晶胞的单面心,以“A”、“B”、“C”表示;晶胞的所有面心上,以 “F”表示;三方晶系晶胞的特殊位置,常以“R”表示;对不能增置阵点或没有增添阵点的 简单晶胞用“P”表示,再考虑满足晶胞体积最小的要求,结果共得14种布喇菲(Bravais) 晶胞,如表22中所列,其具体构形如表23所示。由这些晶胞在空间中的周期堆叠,便构 成布喇菲(Bravais)点阵。 表23 7个晶系14种Bravais晶胞[19] 晶系 单纯格子(P) 底心格子(C) 体心格子(I) 面心格子(F) 1 三斜晶系 (triclinic) 2 单斜晶系 (monoclinic) 3 正交晶系 (orthorhombic) 4 四方晶系 (tetragonal) 5 立方(等轴)晶系 (cubic) 6 菱形晶系 (rhombohedral) (三方晶系) (trigonal) 7 六方晶系 (hexagonal) 214 晶列、晶面及其表示 1.晶列及其表示方法 在空间点阵中通过两阵点的直线,称为点阵直线或晶列。晶列的特征是它的方向性和 周期性。在空间点阵中有一晶列,必有与其平行的无限多条相同的晶列,构成所谓晶列族, · 92 ·