
式中的P,表示电子j的动量,∑表示对全电子体系求和。式1.7.1)的右边的两项分别 表示电子体系的动能和势能。对该体系如果作用以电磁场时,则式(①.7.1)中的P,由于电 磁场的矢势A(y,t)(r,表示电子的位置)的作用,变为P,+eA(,t)。另外,再考虑到 电磁场的能量H,该系全体的H就变为: H>2m(P +eA ()+ 1.7.2) 该式可进一步表示为: H=≥2a+y品A)+A)+L+H,a.73动 要把电子体系做量子力学处理,则作为量子力学的H,需把式1.7.3)中的P,、A(,t) 看做算符,与卫,对应的运算关系为P,仁-gad。一般情况下,算符卫与A(,t)是不 可交换的,但是由于在这里采用了置divA(y,t)=0的Coulomb度规,所以可有P,· A(y,t)=A(y,t)·P,。由式(.7.3)可得电子体系与电磁场的相互作用的milton函数 H=∑AG)+∑mA) 1.7.4) 式1.7.4)为一个微扰Hamilton函数,无相互作用时体系的Hamilton函数变为: H。=H-H=2mP+H.+H, 1.7.5) 成为电子体系与电磁场的能量之和。另外,在处理与电子自旋相关的磁散射和磁Compton 散射时,还要在式1.7.4)里加上与其相关的Hamilton函数。 在式1.7.4)表示的相互作用情况下,电子体系和电磁场的状态应按Schrodinger方 我 器=(H。+g 1.7.6) 随着时间变化,式中©为表征状态的波函数,在把电磁场做经典处理时,©为表示电子体 系的波函数。 根据依存于时间的微扰理论,在一级微扰的情况下,从体系的初态i向终态跃迁,由 矩阵元 Tg=flH'Ii》=pH9dr 1.7.7) 决定,每单位时间从i向f的跃迁几率(Transition Probability)由 aw=1Tg"2pE,)=2爱11H1》PpE,) 1.7.8) 给出,常称之为“费米黄金规则”Fermi's golden rule)。式1.7.8)中的p(E,)为终态的态 密度.在i和f之间遵循能量守恒规则。在2级微扰的情况下,矩阵元由下式给出: T%=yf1H1m)a1H1边 E-E 1.7.9) 这里假设从i→∫跃迁时经过中间状态,在该中间状态中即使能量不守恒也可以,但E ·20·
式中的Pj 表示电子j的动量,∑ j 表示对全电子体系求和。式(171)的右边的两项分别 表示电子体系的动能和势能。对该体系如果作用以电磁场时,则式(171)中的Pj由于电 磁场的矢势A(rj,t)(rj表示j电子的位置)的作用,变为Pj+eA(rj,t)。另外,再考虑到 电磁场的能量 Hr,该系全体的 H 就变为: H = ∑ j 1 2m {Pj +eA(rj,t)}2 +He +Hr (172) 该式可进一步表示为: H = ∑ j 1 2mP2 j +∑ j e mPj·A(rj,t)+∑ j e2 2mA2 (rj,t)+He +Hr (173) 要把电子体系做量子力学处理,则作为量子力学的 H,需把式(173)中的Pj、A(rj,t) 看做算符,与Pj 对应的运算关系为Pj-igrad。一般情况下,算符Pj 与A(rj,t)是不 可交换的,但是由于在这里采用了置divA(rj,t)=0的 Coulomb度规,所以可有 Pj· A(rj,t)=A(rj,t)·Pj。由式(173)可得电子体系与电磁场的相互作用的Hamilton函数: H′= ∑ j e mPj·A(rj,t)+∑ j e2 2mA2 (rj,t) (174) 式(174)为一个微扰 Hamilton函数,无相互作用时体系的 Hamilton函数变为: H0 = H -H′= ∑ j 1 2mP2 j +He +Hr (175) 成为电子体系与电磁场的能量之和。另外,在处理与电子自旋相关的磁散射和磁Compton 散射时,还要在式(174)里加上与其相关的 Hamilton函数。 在式(174)表示的相互作用情况下,电子体系和电磁场的状态应按Schrdinger方 程: iφ t=(H0 +H′)φ (176) 随着时间变化,式中φ为表征状态的波函数,在把电磁场做经典处理时,φ为表示电子体 系的波函数。 根据依存于时间的微扰理论,在一级微扰的情况下,从体系的初态i向终态f跃迁,由 矩阵元 T(1) fi =〈f|H′|i〉≡∫φ fH′φidr (177) 决定,每单位时间从i向f的跃迁几率(TransitionProbability)由 ω =2π |T(1) fi |2 ρ(Ef)=2π |〈f|H′|i〉|2 ρ(Ef) (178) 给出,常称之为“费米黄金规则”(Fermi’sgoldenrule)。式(178)中的ρ(Ef)为终态的态 密度。在i和f之间遵循能量守恒规则。在2级微扰的情况下,矩阵元由下式给出: T(2) fi = ∑n 〈f|H′|n〉〈n|H′|i〉 Ei -En (179) 这里假设从i→f跃迁时经过中间状态n,在该中间状态中即使能量不守恒也可以,但En · 02 ·

~E,的态将成为主要项。在这种情况下,单位时间的跃迁几率可由把式(1.7.8)中的T 换为T%得到。当不仅把电子体系而且把电磁场也做量子化处理时,矢势A由光子的消 灭和生成算符的一次结合表征。这时,式1,7.6)的9成为表征电子体系加电磁场总体的 波函数跃迁几率。表示,在尺度为L3的箱中存在一个入射光子时,单位时间内在立体角 n中散射的光子数,将其换算到在与光子进行方向垂直的单位面积单位时间入射一个光 子的情况下,得微分散射截面为: 1.7.10) 现分下列情况予以讨论。 1.P·A的一级微扰 把相互作用图示,得图1.21。由于表示相互作用的式1.7.4)中的P·A项只与A的 1次方成比例,所以由其导致的一级微扰中仅有一个光子消灭或生成。图1.21()表示与 吸收一个光子的同时,激发一个电子,这对应于光电吸收。图1.216)表示电子退激的同 时,放出一个光子,这对应于荧光X射线的辐射。这些都与被紧束缚的电子有关。 2.A2的一级微扰 式1.7,4)中的A三项,由于它与A的2次方成比例,所以它所导致的一级微扰跟两 个光子的消灭或生成的双光子过程有关。图1.21。即表示与吸收一个光子的同时,放出 一个光子的情况,这与比较自由的电子或弱束缚的电子有关,弹性散射的Thomson散射、 非弹性散射的Compton散射以及Compton-一Raman散射等,与该过程对应。 3.P·A的二级微扰 式1.7.4)的P·A项的二级微扰也与双光子有关。图1.21)所表示的中间状态的 介入相应于一个光子的消灭、一个光子的生成,不过按其顺序可分两种情况。这与强束缚 的电子有关,弹性散射的异常散射、非弹性散射的Raman散射等,都与此过程对应。 图1.21原子中的电子与X射线电磁场相互作用示意图 ·21·
Ei的态将成为主要项。在这种情况下,单位时间的跃迁几率可由把式(178)中的T(1) fi 换为T(2) fi 得到。当不仅把电子体系而且把电磁场也做量子化处理时,矢势 A 由光子的消 灭和生成算符的一次结合表征。这时,式(176)的φ成为表征电子体系加电磁场总体的 波函数。跃迁几率ω表示,在尺度为L3的箱中存在一个入射光子时,单位时间内在立体角 dΩ中散射的光子数,将其换算到在与光子进行方向垂直的单位面积单位时间入射一个光 子的情况下,得微分散射截面为: dσ=L3 cω (1710) 现分下列情况予以讨论。 1. P·A 的一级微扰 把相互作用图示,得图121。由于表示相互作用的式(174)中的P·A 项只与A 的 1次方成比例,所以由其导致的一级微扰中仅有一个光子消灭或生成。图121(a)表示与 吸收一个光子的同时,激发一个电子,这对应于光电吸收。图121(b)表示电子退激的同 时,放出一个光子,这对应于荧光X射线的辐射。这些都与被紧束缚的电子有关。 2. A2 的一级微扰 式(174)中的A二 项,由于它与A 的2次方成比例,所以它所导致的一级微扰跟两 个光子的消灭或生成的双光子过程有关。图121(c)即表示与吸收一个光子的同时,放出 一个光子的情况,这与比较自由的电子或弱束缚的电子有关,弹性散射的 Thomson散射、 非弹性散射的Compton散射以及Compton—Raman散射等,与该过程对应。 3. P·A 的二级微扰 式(174)的P·A 项的二级微扰也与双光子有关。图121(d)所表示的中间状态的 介入相应于一个光子的消灭、一个光子的生成,不过按其顺序可分两种情况。这与强束缚 的电子有关,弹性散射的异常散射、非弹性散射的Raman散射等,都与此过程对应。 穴葬雪 穴遭雪 穴凿雪 穴糟雪 图121 原子中的电子与X射线电磁场相互作用示意图 · 12 ·

在图1.21中,实线表示电子,波线表示光子,初态置于下侧,终态在上侧,(a)一光子 的吸收:6)一光子的辐射:(c)一光子的吸收和一光子的辐射:()介有中间状态的一光 子的吸收和一光子的辐射。 参考文献 [1]A.H.Compton and S.K.Allison X-Ray in Theory and Erperiment,Von Norstrand,New York, 1935. 2R.W.James:The Opicl Principles of Diffraction ofX-Ras,1954. [3]菊田惺志著:《X線回折·散乱技術,束京大学出版会,1992. [4]黄胜涛主编:個体X射线学》(一),高等教育出版社,1985 [5]许顺生著:《金属X射线学》,上海科学技术出版社,1962. [6]Max von Laue Rontgenstrahlinterferferenzen,Akademische Verlag,Leipzig,1960. []高良和武责任编集:《線回折,共立出版,1988 [8]仁田勇监修:0線结晶学》(上),丸善,1959. [9]W.H.Zachariasen:Theory of X-Ray Diffraction in Crystals Wiley,New York,1945. 10]D.舍伍德著,范世藩译:《儡体,X射线和蛋白质》,科学出版社,1985 山1门李树棠编著:儡体X射线衍射学基,冶金工业出版社,1997(再版). 2]Γ.5.柏基意苏联),M.A.巴赖柯希志(苏联)合著,施士元译:《伦琴射线结构分析实用教 ,高等教育出版社,1954 3]周公度,郭可信:儡体和准晶体的衍射》,北京大学出版社,1999. 14]A.H.KHTaropocKH(苏联)著,龚尧圭等译:《K射线结构分析》,科学出版社,1958. 15]旧本物理学会编(佐々木泰三:办]懒筆):《>夕口卜口>放射》,培風馆,1986. [16]M.Nielsen Z.Phys.,B61,(1985),415. 17]L.G.Parratt:Phy%.Rev.,95,(1954),359. [18]M.Ashkin,M.Kuriyama:J.Phys.Soc.Japan,21,(1966),1549 [19]M.Kuriyama:J.Phys.Soc.Japan,23,(1967),1369:25,(1968),848 [20]M.Kuriyama:Acta Cryst..,A27,1971),634:A28,1972),588. [21]Y.H.Ohtsuki,S.Yanagawa J.Phys.Soc.Japan,21.(1966),502 ·22·
在图1.21中,实线表示电子,波线表示光子,初态置于下侧,终态在上侧,(a)一光子 的吸收;(b)一光子的辐射;(c)一光子的吸收和一光子的辐射;(d)介有中间状态的一光 子的吸收和一光子的辐射。 参 考 文 献 [1]A.H.ComptonandS.K.Allison:X-RayinTheoryandExperiment,VonNorstrand,NewYork, 1935. [2]R.W.James:TheOpticalPrinciplesofDiffractionofX-Rays,Bell&Sons,London,1954. [3]菊田惺志著 :《X辌回折·散乱技术》,东京大学出版会,1992. [4]黄胜涛主编 :《固体X射线学》(一),高等教育出版社,1985. [5]许顺生著 :《金属X射线学》,上海科学技术出版社,1962. [6]MaxvonLaue:Rntgenstrahlinterferferenzen,AkademischeVerlag,Leipzig,1960. [7]高良和武责任编集 :《X辌回折》,共立出版,1988. [8]仁田勇监修 :《X辌结晶学》(上),丸善,1959. [9]W.H.Zachariasen:TheoryofX-RayDiffractioninCrystals,Wiley,NewYork,1945. [10]D.舍伍德著,范世藩译 :《晶体,X 射线和蛋白质》,科学出版社,1985. [11]李树棠编著 :《晶体X 射线衍射学基础》,冶金工业出版社,1997(再版). [12]Г.Б.柏基意(苏联),М.А.巴赖柯希志(苏联)合著,施士元译 :《伦琴射线结构分析实用教 程》,高等教育出版社,1954. [13]周公度,郭可信 :《晶体和准晶体的衍射》,北京大学出版社,1999. [14]А.И.Китайгородский(苏联)著,龚尧圭 等译 :《X 射线结构分析》,科学出版社,1958. [15]日本物理学会编(佐々木泰三[ほか]执笔):《シンクロトロン放射》,培风馆,1986. [16]M.Nielsen:Z.Phys.,B61,(1985),415. [17]L.G.Parratt:Phys.Rev.,95,(1954),359. [18]M.Ashkin,M.Kuriyama:J.Phys.Soc.Japan,21,(1966),1549. [19]M.Kuriyama:J.Phys.Soc.Japan,23,(1967),1369;25,(1968),848. [20]M.Kuriyama:ActaCryst.,A27,(1971),634;A28,(1972),588. [21]Y.H.Ohtsuki,S.Yanagawa:J.Phys.Soc.Japan,21,(1966),502. · 22 ·

第二章 物质结构基础 X射线分析研究的物质结构是原子尺度以上的层次。在这个层次中,可将物质结构 粗略地分为非晶结构和晶态结构两大类。现在人们又把分形、准晶和纳米态也考虑进来, 可见,不管怎样分类都包含一定的模糊性。限于篇幅,本书只讨论:晶体结构、准晶、分形 和仲晶结构、表面和薄膜结构以及非晶结构。这方面国内外的成书很多-],读者可以 从中看到更详尽的内容。 2.1晶体结构 2.1.1晶体、空间点阵、晶体结构0-刀 众所周知,最初人们是从晶体美丽规则的外形抽象出它的对称性,推断其周期构成 的,后来科学的发展证实了这种推断。所以,准确地说,晶体就是其构成原子(离子、分子 或其集合)在空间作周期排列而构成的物质。 图2.1空间点阵及空间格子 图2.1()为晶体平面结构的示意图,图中的”为其构成的基本要素,称为基元。 在各基元上选定相应的点,构成一个空间阵列,称为空间点阵。把空间点阵的诸阵点用直 线连接起来,构成空间格子,也称晶格。如图2.16)所示。这样,即可用模式 晶体结构=空间点阵+基元 2.1.1) 来描述晶体结构了。空间点阵是数学的抽象,在描述晶体结构时,勿忘在空间中它在各个 。23
第二章 物质结构基础 X射线分析研究的物质结构是原子尺度以上的层次。在这个层次中,可将物质结构 粗略地分为非晶结构和晶态结构两大类。现在人们又把分形、准晶和纳米态也考虑进来, 可见,不管怎样分类都包含一定的模糊性。限于篇幅,本书只讨论:晶体结构、准晶、分形 和仲晶结构、表面和薄膜结构以及非晶结构。这方面国内外的成书很多[1-19] ,读者可以 从中看到更详尽的内容。 21 晶体结构 211 晶体、空间点阵、晶体结构[1-7] 众所周知,最初人们是从晶体美丽规则的外形抽象出它的对称性,推断其周期构成 的,后来科学的发展证实了这种推断。所以,准确地说,晶体就是其构成原子(离子、分子 或其集合)在空间作周期排列而构成的物质。 穴葬雪 穴遭雪 图21 空间点阵及空间格子 图21(a)为晶体平面结构的示意图,图中的“ ”为其构成的基本要素,称为基元。 在各基元上选定相应的点,构成一个空间阵列,称为空间点阵。把空间点阵的诸阵点用直 线连接起来,构成空间格子,也称晶格。如图2.1(b)所示。这样,即可用模式 晶体结构 = 空间点阵+基元 (211) 来描述晶体结构了。空间点阵是数学的抽象,在描述晶体结构时,勿忘在空间中它在各个 · 32 ·
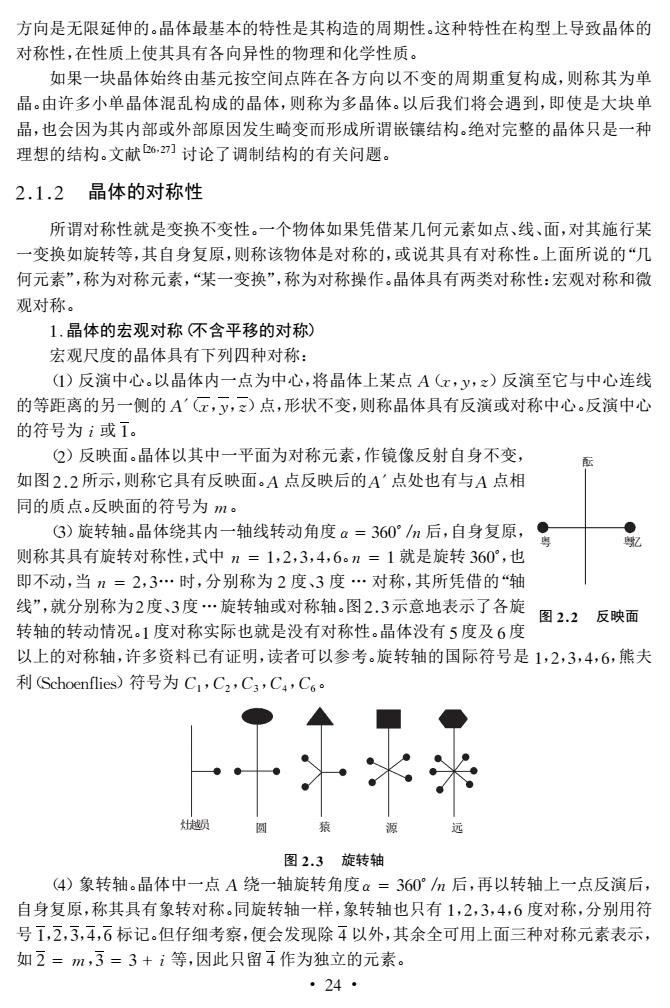
方向是无限延伸的。晶体最基本的特性是其构造的周期性。这种特性在构型上导致晶体的 对称性,在性质上使其具有各向异性的物理和化学性质。 如果一块晶体始终由基元按空间点阵在各方向以不变的周期重复构成,则称其为单 晶。由许多小单晶体混乱构成的晶体,则称为多晶体。以后我们将会遇到,即使是大块单 晶,也会因为其内部或外部原因发生畸变而形成所谓嵌镶结构。绝对完整的晶体只是一种 理想的结构。文献刃讨论了调制结构的有关问题。 2.1.2晶体的对称性 所谓对称性就是变换不变性。一个物体如果凭借某几何元素如点、线、面,对其施行某 一变换如旋转等,其自身复原,则称该物体是对称的,或说其具有对称性。上面所说的“几 何元素”,称为对称元素,“某一变换”,称为对称操作。晶体具有两类对称性:宏观对称和微 观对称。 1.晶体的宏观对称不含平移的对称) 宏观尺度的晶体具有下列四种对称: I)反演中心。以晶体内一点为中心,将晶体上某点A(x,y,z)反演至它与中心连线 的等距离的另一侧的A'云,y,)点,形状不变,则称晶体具有反演或对称中心。反演中心 的符号为i或ī。 2)反映面。晶体以其中一平面为对称元素,作镜像反射自身不变, 如图2.2所示,则称它具有反映面。A点反映后的A'点处也有与A点相 同的质点。反映面的符号为m。 3)旋转轴。晶体绕其内一轴线转动角度a=360°/m后,自身复原, 则称其具有旋转对称性,式中n=1,2,3,4,6。n=1就是旋转360°,也 即不动,当n=2,3…时,分别称为2度、3度…对称,其所凭借的“轴 线”,就分别称为2度、3度…旋转轴或对称轴。图2.3示意地表示了各旋 图2.2反映面 转轴的转动情况。1度对称实际也就是没有对称性。晶体没有5度及6度 以上的对称轴,许多资料已有证明,读者可以参考。旋转轴的国际符号是1,2,3,4,6,熊夫 利(Schoenflies)符号为C,C2,C3,C4,C6。 米米 图2.3旋转轴 (4)象转轴。晶体中一点A绕一轴旋转角度α=360°/m后,再以转轴上一点反演后, 自身复原,称其具有象转对称。同旋转轴一样,象转轴也只有1,2,3,4,6度对称,分别用符 号1,2,3,4,石标记。但仔细考察,便会发现除4以外,其余全可用上面三种对称元素表示, 如2=m,3=3+i等,因此只留4作为独立的元素 ·24·
方向是无限延伸的。晶体最基本的特性是其构造的周期性。这种特性在构型上导致晶体的 对称性,在性质上使其具有各向异性的物理和化学性质。 如果一块晶体始终由基元按空间点阵在各方向以不变的周期重复构成,则称其为单 晶。由许多小单晶体混乱构成的晶体,则称为多晶体。以后我们将会遇到,即使是大块单 晶,也会因为其内部或外部原因发生畸变而形成所谓嵌镶结构。绝对完整的晶体只是一种 理想的结构。文献[26,27]讨论了调制结构的有关问题。 212 晶体的对称性 所谓对称性就是变换不变性。一个物体如果凭借某几何元素如点、线、面,对其施行某 一变换如旋转等,其自身复原,则称该物体是对称的,或说其具有对称性。上面所说的“几 何元素”,称为对称元素,“某一变换”,称为对称操作。晶体具有两类对称性:宏观对称和微 观对称。 1.晶体的宏观对称(不含平移的对称) 宏观尺度的晶体具有下列四种对称: (1)反演中心。以晶体内一点为中心,将晶体上某点A(x,y,z)反演至它与中心连线 的等距离的另一侧的A′(x,y,z)点,形状不变,则称晶体具有反演或对称中心。反演中心 的符号为i或1。 酝 粤 粤忆 图22 反映面 (2)反映面。晶体以其中一平面为对称元素,作镜像反射自身不变, 如图22所示,则称它具有反映面。A 点反映后的A′点处也有与A 点相 同的质点。反映面的符号为 m。 (3)旋转轴。晶体绕其内一轴线转动角度α=360°/n后,自身复原, 则称其具有旋转对称性,式中n =1,2,3,4,6。n =1就是旋转360°,也 即不动,当n =2,3… 时,分别称为2度、3度 … 对称,其所凭借的“轴 线”,就分别称为2度、3度 … 旋转轴或对称轴。图23示意地表示了各旋 转轴的转动情况。1度对称实际也就是没有对称性。晶体没有5度及6度 以上的对称轴,许多资料已有证明,读者可以参考。旋转轴的国际符号是1,2,3,4,6,熊夫 利(Schoenflies)符号为C1,C2,C3,C4,C6。 灶越员 圆 猿 源 远 图23 旋转轴 (4)象转轴。晶体中一点A 绕一轴旋转角度α=360°/n后,再以转轴上一点反演后, 自身复原,称其具有象转对称。同旋转轴一样,象转轴也只有1,2,3,4,6度对称,分别用符 号1,2,3,4,6标记。但仔细考察,便会发现除4以外,其余全可用上面三种对称元素表示, 如2= m,3=3+i等,因此只留4作为独立的元素。 · 42 ·