
Compton散射的总截面为: =292-a2]h0去20-+0 2a 1+2a 1.4.16) 式中a=方w/(m).将固体中的电子以自由电子加以处理,则可由散射线能量的精确测 定,得到固体内电子动量分布的信息。如果用圆偏振光X射线作用于磁性固体,则可通过 磁性Compton散射求得磁性电子的动量分布及磁矩等信息。对于轻元素束缚较强的内层 电子,常常发生Raman散射。一般地说,电子受束缚的程度由其与X射线光子能量的比较 而定。如果把电子的结合能以其平均轨道半径α表示,则可把散射分为: 电子受束缚的程度 散射类型 >1比较自由状态 Compton散射 红sin0之1弱束缚状态 入 Compton-一Raman散射 (≤1强束缚状态 Raman散射 以Cu的K。线为例,它对Li的1S电子当散射角20小的时候,属Raman散射,当0变大 则为Compton-一Raman散射:而对Li的2S电子,则不论0如何均为Compton散射。 1.4.3X射线的衍射 下一章将讲到,晶体是由原子或原子团在空间周期排列构成的。原子的排列构成晶 格,晶格格点间距恰与X射线的波长属同一量级,对于X射线的入射,晶体犹如一个衍射 光栅。当沿某方向散射的波位相一致、互相加强时,则发生“衍射”,也常把这种衍射称为 “反射”。 图1.16Brgg方程的推演 现就图1.16考察一下发生衍射的条件。设波长为入的X射线入射到一族间距为d的 原子面上,则对于上面第一层原子面[如图1.16(a)所示],只要入射线与散射线同原子面 间的夹角相等,各散射波的位相总是一致的而且可以互相加强:对于第二层原子面[图1. 16b)所示]只要它与相邻原子面的散射线间的光程差2 sine0g为波长的整数倍,即: 2dwsineB na 1.4.17) 时,则不论各层原子面上的原子是否上下对齐,其位相也是一致的,散射波相互加强,发生 衍射.式(1.4.17)称为“Bragg”条件或“Bragg”方程,0a称为Bragg角,n为反射级数,即是 面间距为d灿的(kl)晶面的n级反射.如果把Brgg方程改写为: 2 dsi0=入 1.4.18) ·15·
Compton散射的总截面为: σc =2πr2 e 1+a a2 2(1+a) 1+2a -ln(1+2a) [ ] a +ln(1+2a) 2a - 1+3a { } (1+2a)2 (1416) 式中a =ω/(mc2)。将固体中的电子以自由电子加以处理,则可由散射线能量的精确测 定,得到固体内电子动量分布的信息。如果用圆偏振光 X射线作用于磁性固体,则可通过 磁性Compton散射求得磁性电子的动量分布及磁矩等信息。对于轻元素束缚较强的内层 电子,常常发生Raman散射。一般地说,电子受束缚的程度由其与X射线光子能量的比较 而定。如果把电子的结合能以其平均轨道半径α表示,则可把散射分为: 电子受束缚的程度 散射类型 4πα λ0 sinθ 1比较自由状态 1弱束缚状态 1 烅 烄 烆 强束缚状态 Compton散射 Compton—Raman散射 Raman散射 以Cu的 Kα 线为例,它对Li的1S 电子当散射角2θ小的时候,属Raman散射,当θ变大 则为Compton—Raman散射;而对Li的2S 电子,则不论θ如何均为Compton散射。 143 X射线的衍射 下一章将讲到,晶体是由原子或原子团在空间周期排列构成的。原子的排列构成晶 格,晶格格点间距恰与X射线的波长属同一量级,对于X射线的入射,晶体犹如一个衍射 光栅。当沿某方向散射的波位相一致、互相加强时,则发生“衍射”,也常把这种衍射称为 “反射”。 孕 匝忆 孕忆 假想 凿穴澡噪造雪辕灶晶面 圆 员 穴葬雪 穴遭雪 穴糟雪 凿穴澡噪造雪 θ θ忆 θ θ忆 砸忆 砸 匝 月 月 月 圆 员 员 圆 图116 Bragg方程的推演 现就图116考察一下发生衍射的条件。设波长为λ的X射线入射到一族间距为d的 原子面上,则对于上面第一层原子面[如图1.16(a)所示],只要入射线与散射线同原子面 间的夹角相等,各散射波的位相总是一致的而且可以互相加强;对于第二层原子面[图1. 16(b)所示]只要它与相邻原子面的散射线间的光程差2dhklsinθB 为波长的整数倍,即: 2dhklsinθB =nλ (1417) 时,则不论各层原子面上的原子是否上下对齐,其位相也是一致的,散射波相互加强,发生 衍射。式(1417)称为“Bragg”条件或“Bragg”方程,θB 称为Bragg角,n为反射级数,即是 面间距为dhkl 的(hkl)晶面的n级反射。如果把Bragg方程改写为: 2dhkl nsinθB =λ (1418) · 51 ·

则可认为式1.4.18)为面间距为=d的晶面的一级反射[如图1.16@所示],常 称指数(hnkl)为衍射面指数,它只是一个假想的“晶面”。 如果把X射线在晶体内部的折射也予考虑,则对于一个与晶体表面平行的衍射面的 Bragg方程应严格地表示为: 2dusind (1sin )=nd (1.4.19) 其中,6如式1.3.8)和(.3.9)所示。 1.5光电效应与二次辐射 光电效应是X射线与物质的又一种相互作用,在一般情况下,它是X射线光子把自身 能量转移给原子内受束缚的电子、使之受激飞脱受束缚的状态,而X射线光子自身也随之 消灭的一种现象。动量守恒原则在包括原子核的体系内也真,受束缚越强的电子其所呈现 的光电效应越大。一般K壳层电子对光电效应的贡献约占80%,其次是L壳层电子的贡 献等。把X射线通过光电效应击出的电子称为X射线光电子。原子序数为Z的原子的K壳 层电子的结合能大体为: 1.5.1) 其中,ag=hme为Bohr半径,a=e伍c=为精细结构常数。 运光电子 记运兹蓝粤电子 载线 激发过程 辐射跃迁 非辐射跃迁 图1.17X射线对原子的激发与退激过程 图1.17示意地表出K电子的激发过程。X射线光子的能量除一部分用于克服K电子 的结合能外,其余转变为K光电子的动能,即K光电子的动能E为: Eko=h w-Ek 1.5.2) 另一方面,失去K电子的激发态,在回复到稳定态时,K壳层外侧的电子要向空位的K壳 层跃迁。其中又分两种情况:辐射跃迁和非辐射跃迁。对于重原子辐射跃迁的几率较大,跃 迁后跃迁电子将其在两壳层的结合能之差以特征X射线放出,称为“荧光X射线”:在非辐 射跃迁中,跃迁电子的多余能量通过Coulomb作用被其附近的别的电子夺取而飞出,称这 ·16·
则可认为式(1418)为面间距为dhkl n =dnhnknl的晶面的一级反射[如图1.16(c)所示],常 称指数(nhnknl)为衍射面指数,它只是一个假想的“晶面”。 如果把X射线在晶体内部的折射也予考虑,则对于一个与晶体表面平行的衍射面的 Bragg方程应严格地表示为: 2dhklsinθB (1- δ sin2 θB )=nλ (1419) 其中,δ如式(138)和(139)所示。 15 光电效应与二次辐射 光电效应是X射线与物质的又一种相互作用,在一般情况下,它是X射线光子把自身 能量转移给原子内受束缚的电子、使之受激飞脱受束缚的状态,而X射线光子自身也随之 消灭的一种现象。动量守恒原则在包括原子核的体系内也真,受束缚越强的电子其所呈现 的光电效应越大。一般 K壳层电子对光电效应的贡献约占80%,其次是L壳层电子的贡 献等。把X射线通过光电效应击出的电子称为X射线光电子。原子序数为Z的原子的K壳 层电子的结合能大体为: EK ≈e2 Z2 2aB = mc2 2a2 Z2 (151) 其中,aB =2 /me2 为Bohr半径,a =e2/c= 1 137为精细结构常数。 激发过程 运蕴员蕴Ⅲ粤怎早藻则电子 蕴Ⅲ 蕴Ⅰ 蕴Ⅱ 载线 运光电子 运 辐射跃迁 非辐射跃迁 运α员特性 载射线 穴荧光 载射线雪 图117 X射线对原子的激发与退激过程 图117示意地表出K电子的激发过程。X射线光子的能量除一部分用于克服K电子 的结合能外,其余转变为 K光电子的动能,即 K光电子的动能EKo 为: EKo =ω-EK (152) 另一方面,失去 K电子的激发态,在回复到稳定态时,K壳层外侧的电子要向空位的K 壳 层跃迁。其中又分两种情况:辐射跃迁和非辐射跃迁。对于重原子辐射跃迁的几率较大,跃 迁后跃迁电子将其在两壳层的结合能之差以特征X射线放出,称为“荧光X射线”;在非辐 射跃迁中,跃迁电子的多余能量通过Coulomb作用被其附近的别的电子夺取而飞出,称这 · 61 ·

种电子为“Aug©r电子”.在图117中,L子层的电子向K层空位跃迁.L,子层的电子得到 其跃迁能变为Auger电子,称为L,L,Auger电子,它的动能可表示为: EA=(EK-E)-ELn÷EK-2E 1.5.3) 其中EKELEuE,分别表示K壳层、L壳层、L子壳层和处于离子化关态的L子 壳层电子的结合能。 二次辐射可用来评价物质。例如XPSX-Ray photoelectron Spectroscopy)法和 ESCA(Electron Spectroscopy for Chemical Analysis)法等。通过测定X射线光电子能量,可 以对固体表面层存在的元素及其结合状态进行分析:荧光X射线可对物质中的元素作分 析:另外还有Auger电子分光(Auger Electron Spectroscopy)法,也可用来做固体表面层元 素的定性及结合状态的分析。 1.6X射线的吸收 X射线通过物质时,如图1.18所示,将发生一复杂的过程,现分别讨论下列两个问 · 4A 散射我射线散射等 非弹性散射 片散射等雪 ,荧光载射线 入射载射线 ·透射载射线 光电子、电子、 反冲电子 欢电子 物质 图1.18X射线通过物质过程中的各种效应 1.6.1吸收系数 一定波长的X射线通过物质时,其强度的减少与所通过的距离成比例,若强度为I的 X射线通过厚度为dx的物质后,其减少量为dI,则有: -dI =udx 1.6.1) 其中,红为比例系数(称为线吸收系数).积分式1.6.1)可得: I=Ioexp(-x) 1.6.2) 其中,1。为入射线的原强度,x为X射线通过的物质厚度。通过厚x的物质后,X射线的强 度变为1,线吸收系数:[m1]不仅与X射线的波长和物质有关,而且对同一种物质也因 其凝聚状态不同而异。所以,为了方便,又引入了:[mKg](p为物质的密度),称为 。17
种电子为“Auger电子”。在图117中,L1子层的电子向K层空位跃迁。LⅢ 子层的电子得到 其跃迁能变为Auger电子,称为L1LⅢAuger电子,它的动能可表示为: EAuger =(EK -EL1 )-EL ′ Ⅲ EK -2EL (153) 其中EK、EL、EL1 、EL ′ Ⅲ 分别表示K壳层、L壳层、L子壳层和处于离子化关态的L ′ Ⅲ 子 壳层电子的结合能。 二次辐 射 可 用 来 评 价 物质。例 如 XPS(X-RayphotoelectronSpectroscopy)法 和 ESCA(ElectronSpectroscopyforChemicalAnalysis)法等。通过测定X射线光电子能量,可 以对固体表面层存在的元素及其结合状态进行分析;荧光 X射线可对物质中的元素作分 析;另外还有Auger电子分光(AugerElectronSpectroscopy)法,也可用来做固体表面层元 素的定性及结合状态的分析。 16 X射线的吸收 X射线通过物质时,如图118所示,将发生一复杂的过程,现分别讨论下列两个问 题。 热 物质 反冲电子 光电子、粤怎早藻则电子、妖电子 穴悦燥皂责贼燥灶散射等雪 穴栽澡燥皂泽燥灶散射等雪 非弹性散射 妖弹性散射 荧光 载射线 入射 载射线 散射 载射线 透射 载射线 图118 X射线通过物质过程中的各种效应 161 吸收系数 一定波长的X射线通过物质时,其强度的减少与所通过的距离成比例,若强度为I的 X射线通过厚度为dx的物质后,其减少量为dI,则有: -dI I =μdx (161) 其中,μ为比例系数(称为线吸收系数)。积分式(161)可得: I=I0exp(-μx) (162) 其中,I0为入射线的原强度,x为X射线通过的物质厚度。通过厚x的物质后,X射线的强 度变为I,线吸收系数μ[m-1]不仅与X射线的波长和物质有关,而且对同一种物质也因 其凝聚状态不同而异。所以,为了方便,又引入了μ/ρ[m2 Kg-1](ρ为物质的密度),称为 · 71 ·

“质量吸收系数”。这样式1.6.2)又可表示为: I=1exp(r) (1.6.3) 混合物、化合物的质量吸收系数,可用各成分的质量吸收系数及重量百分率表示为: L=1lp)x1+2)x2+… 0 100 1.6.4 式中x1,x2…为元素的重量百分率。对于分子式为AxBy…的化合物可以表示为: 长=)ax+sls)by+ a.x+by+… 1.6.5) 式中a,b…分别为元素A,B…的原子量。 X射线的吸收,包含着X射线和物质各种相互作用,如图1.18所示。对于线吸收系数 还可以分为真吸收和散射吸收两部分。真吸收包括光电效应和Compton散射中反冲电子 所导致的吸收:散射吸收包括Thomson散射及Compton散射所引起的吸收.以铁的线吸收 系数为例,如图1.19。 撒射 园 首 电子对生成 能量演 图1.19铁的线吸收系数随X射线能量的变化与 各种相互作用对:的贡献 从图可知,在不同的X光子能区,各种吸收对线吸收系数的贡献是不一样的。在X射 线光电子能量超过静止电子能量2倍(.02MV)时,X射线光子的能量转换为电子和正 电子对,而正电子又与电子结合变为光子。 1.6.2吸收曲线 以光电效应为主要贡献的吸收系数与X射线波长的关系如图1.20所示,其中有若干 个峰,常称之为吸收限。它的形成是X射线光子的能量达到足以击出受照物质中某元素的 K、L等壳层的电子时,所发生的共振吸收。形成吸收限所需要的能量与各壳层电子的结合 能有关,设入为吸收限波长、Eg为结合能,则有: ·18·
“质量吸收系数”。这样式(162)又可表示为: I=I0exp(-μ ρρx) (163) 混合物、化合物的质量吸收系数,可用各成分的质量吸收系数及重量百分率表示为: μ ρ =(μ1/ρ1)x1 +(μ2/ρ2)x2 +… 100 (164) 式中x1,x2… 为元素的重量百分率。对于分子式为AxBy… 的化合物可以表示为: μ ρ =(μA/ρA)ax+(μB/ρB)by+… ax+by+… (165) 式中a,b… 分别为元素A,B… 的原子量。 X射线的吸收,包含着X射线和物质各种相互作用,如图118所示。对于线吸收系数 还可以分为真吸收和散射吸收两部分。真吸收包括光电效应和Compton散射中反冲电子 所导致的吸收;散射吸收包括Thomson散射及Compton散射所引起的吸收。以铁的线吸收 系数为例,如图119。 线 吸 收 系 数 眼皂原员演 员园园 员缘园 栽澡燥皂泽燥灶散射 能量眼噪藻灾演 员园 圆园 缘园 员园园 圆园园 缘园园员园园园 圆园园园 缘园园园 μ 电子对生成 园 缘园 光电效应 悦燥皂责贼燥灶散射 图119 铁的线吸收系数随X射线能量的变化与 各种相互作用对μ的贡献 从图可知,在不同的X光子能区,各种吸收对线吸收系数的贡献是不一样的。在 X射 线光电子能量超过静止电子能量2倍(102MeV)时,X射线光子的能量转换为电子和正 电子对,而正电子又与电子结合变为光子。 162 吸收曲线 以光电效应为主要贡献的吸收系数与X射线波长的关系如图120所示,其中有若干 个峰,常称之为吸收限。它的形成是X射线光子的能量达到足以击出受照物质中某元素的 K、L等壳层的电子时,所发生的共振吸收。形成吸收限所需要的能量与各壳层电子的结合 能有关,设λabs 为吸收限波长、EB 为结合能,则有: · 81 ·
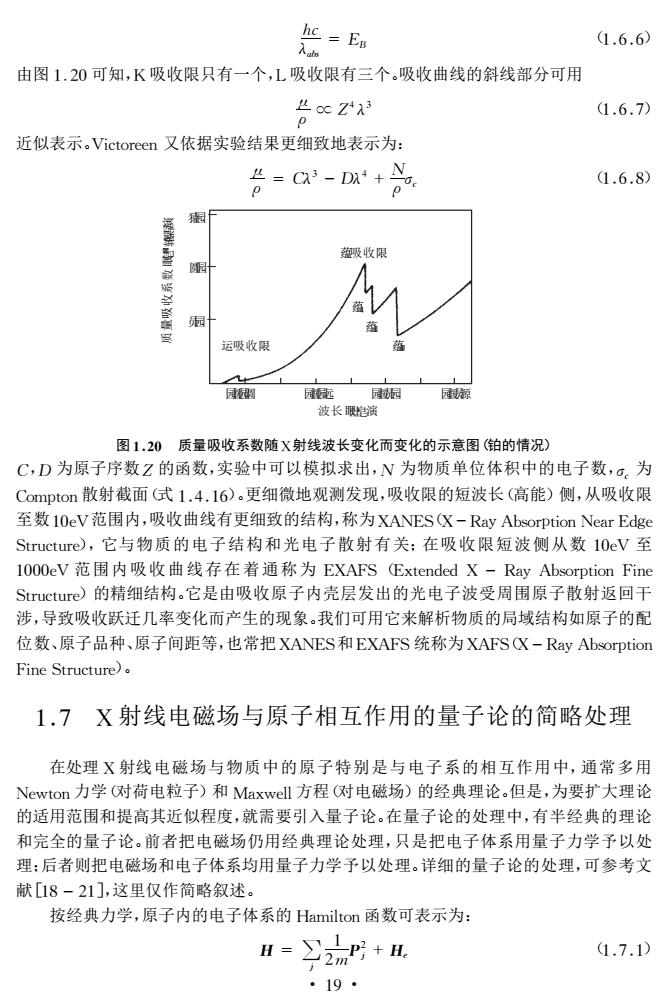
hc =En 1.6.6) 由图1.20可知,K吸收限只有一个,L吸收限有三个。吸收曲线的斜线部分可用 L oc Zi3 1.6.7) 近似表示。Victoreen又依据实验结果更细致地表示为 1.6.8) 园F 拉吸收限 园 园 运吸收限 图1.20质量吸收系数随X射线波长变化而变化的示意图(铂的情况) C,D为原子序数Z的函数,实验中可以模拟求出,N为物质单位体积中的电子数,。,为 Compton散射截面式1.4.16)。更细微地观测发现,吸收限的短波长(高能)侧,从吸收限 至数1OeV范围内,吸收曲线有更细致的结构,称为XANES(X-Ray Absorption Near Edge Structure),它与物质的电子结构和光电子散射有关:在吸收限短波侧从数1OeV至 1000eV范围内吸收曲线存在着通称为EXAFS(Extended X-Ray Absorption Fine Structure)的精细结构。它是由吸收原子内壳层发出的光电子波受周围原子散射返回干 涉,导致吸收跃迁几率变化而产生的现象。我们可用它来解析物质的局域结构如原子的配 位数、原子品种、原子间距等,也常把XANES和EXAFS统称为XAFSCX-Ray Absorption Fine Structure). 1.7X射线电磁场与原子相互作用的量子论的简略处理 在处理X射线电磁场与物质中的原子特别是与电子系的相互作用中,通常多用 Newton力学(对荷电粒子)和Maxwell方程(G对电磁场)的经典理论,但是,为要扩大理论 的适用范围和提高其近似程度,就需要引入量子论。在量子论的处理中,有半经典的理论 和完全的量子论。前者把电磁场仍用经典理论处理,只是把电子体系用量子力学予以处 理:后者则把电磁场和电子体系均用量子力学予以处理。详细的量子论的处理,可参考文 献18-21],这里仅作简略叙述。 按经典力学,原子内的电子体系的Hamilton函数可表示为: ”2+红 1.7.1) ·19
hc λabs =EB (166) 由图1.20可知,K吸收限只有一个,L吸收限有三个。吸收曲线的斜线部分可用 μ ρ ∝Z4 λ3 (167) 近似表示。Victoreen又依据实验结果更细致地表示为: μ ρ =Cλ3 -Dλ4 +N ρ σc (168) 园援园圆 园援园远 园援员园 园援员源 波长眼灶皂演 蕴吸收限 蕴Ⅰ 蕴Ⅱ 蕴Ⅲ 猿园 圆园 员园 质 量 吸 收 系 数 眼皂圆辕噪早演 运吸收限 图120 质量吸收系数随X射线波长变化而变化的示意图(铂的情况) C,D 为原子序数Z 的函数,实验中可以模拟求出,N 为物质单位体积中的电子数,σc 为 Compton散射截面(式1416)。更细微地观测发现,吸收限的短波长(高能)侧,从吸收限 至数10eV范围内,吸收曲线有更细致的结构,称为XANES(X-RayAbsorptionNearEdge Structure),它与物质的电子结构和光电子散射有关;在吸收限短波侧从数10eV 至 1000eV 范围内吸收曲线存在着通称为 EXAFS(ExtendedX- RayAbsorptionFine Structure)的精细结构。它是由吸收原子内壳层发出的光电子波受周围原子散射返回干 涉,导致吸收跃迁几率变化而产生的现象。我们可用它来解析物质的局域结构如原子的配 位数、原子品种、原子间距等,也常把XANES和EXAFS统称为XAFS(X-RayAbsorption FineStructure)。 17 X射线电磁场与原子相互作用的量子论的简略处理 在处理X射线电磁场与物质中的原子特别是与电子系的相互作用中,通常多用 Newton力学(对荷电粒子)和 Maxwell方程(对电磁场)的经典理论。但是,为要扩大理论 的适用范围和提高其近似程度,就需要引入量子论。在量子论的处理中,有半经典的理论 和完全的量子论。前者把电磁场仍用经典理论处理,只是把电子体系用量子力学予以处 理;后者则把电磁场和电子体系均用量子力学予以处理。详细的量子论的处理,可参考文 献[18-21],这里仅作简略叙述。 按经典力学,原子内的电子体系的 Hamilton函数可表示为: H = ∑ j 1 2mP2 j +He (171) · 91 ·