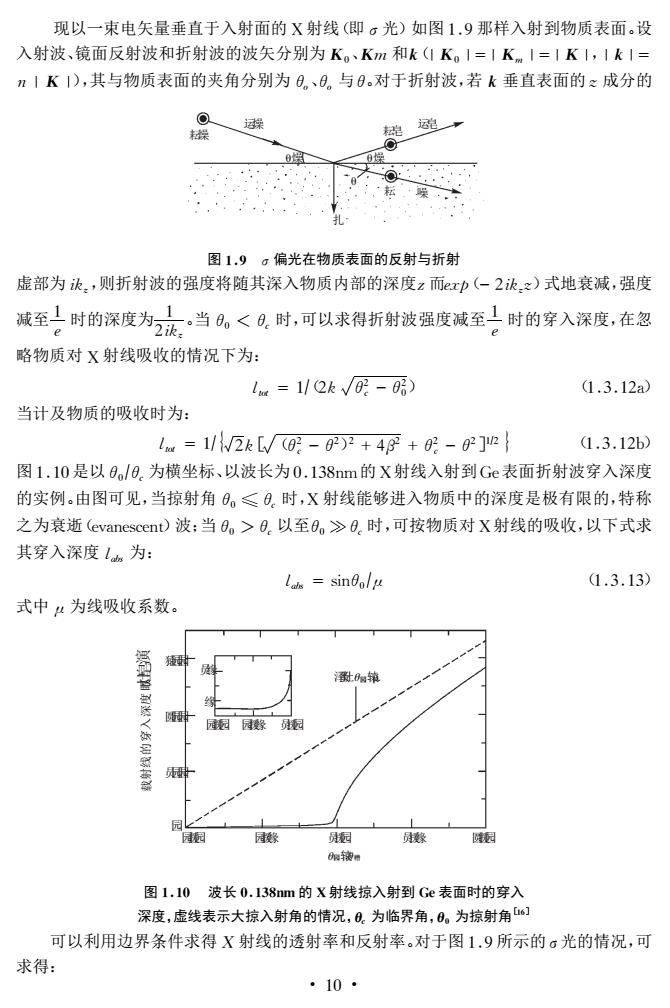
现以一束电矢量垂直于入射面的X射线(即。光)如图1.9那样入射到物质表面。设 入射波、镜面反射波和折射波的波矢分别为K。、Km和k(IK。I=IK,I=IKI,IkI= n1K1),其与物质表面的夹角分别为0。、0。与0。对于折射波,若k垂直表面的:成分的 图1.9。偏光在物质表面的反射与折射 虚部为汲,则折射波的强度将随其深入物质内部的深度z而exp(-2次z)式地衰减,强度 减至上时的深度为证当。<日时,可以求得折射波强度减至上时的穿入深度,在忽 略物质对X射线吸收的情况下为: la=1/2k√0-) 1.3.12a) 当计及物质的吸收时为: l=1/2k[(0-0)2+4g+g-02]} 1.3.12b 图1.10是以0。/0.为横坐标、以波长为0.138nm的X射线入射到Ge表面折射波穿入深度 的实例。由图可见,当掠射角0。≤日,时,X射线能够进入物质中的深度是极有限的,特称 之为衰逝(evanescent)波:当0。>0.以至0。>0.时,可按物质对X射线的吸收,以下式求 其穿入深度为: (1.3.13) 式中:为线吸收系数。 园厨园 图1.10波长0.l38nm的X射线掠入射到Ge表面时的穿入 深度,虚线表示大掠入射角的情况,Q。为临界角,0。为掠射角] 可以利用边界条件求得X射线的透射率和反射率。对于图1.9所示的。光的情况,可 求得: ·10·
现以一束电矢量垂直于入射面的X射线(即σ光)如图19那样入射到物质表面。设 入射波、镜面反射波和折射波的波矢分别为K0、Km 和k(|K0|=|Km|=|K|,|k|= n|K|),其与物质表面的夹角分别为θo、θo 与θ。对于折射波,若k垂直表面的z成分的 耘皂 θ燥 θ燥 θ 运燥 运皂 耘燥 扎 耘 噪 图19 σ偏光在物质表面的反射与折射 虚部为ikz,则折射波的强度将随其深入物质内部的深度z而exp(-2ikzz)式地衰减,强度 减至1 e 时的深度为 1 2ikz 。当θ0 <θc 时,可以求得折射波强度减至1 e 时的穿入深度,在忽 略物质对X射线吸收的情况下为: ltot =1?(2k θ2 槡c -θ2 0) (1312a) 当计及物质的吸收时为: ltot =1?槡2k[ (θ2 c -θ2)2 槡 +4β 2 +θ2 c -θ { } 2]1?2 (1312b) 图110是以θ0?θc为横坐标、以波长为0138nm的X射线入射到Ge表面折射波穿入深度 的实例。由图可见,当掠射角θ0 ≤θc 时,X射线能够进入物质中的深度是极有限的,特称 之为衰逝(evanescent)波;当θ0 >θc以至θ0 θc时,可按物质对X射线的吸收,以下式求 其穿入深度labs 为: labs =sinθ0?μ (1313) 式中μ为线吸收系数。 泽蚤灶θ园辕μ 员缘 园援园 园援缘 员援园 缘 员园园 载 射 线 的 穿 入 深 度 眼灶皂演 猿园园 圆园园 员援缘 θ园辕θ糟 园援园 园援缘 员援园 圆援园 园 图110 波长0138nm的X射线掠入射到Ge表面时的穿入 深度,虚线表示大掠入射角的情况,θc 为临界角,θ0 为掠射角[16] 可以利用边界条件求得X 射线的透射率和反射率。对于图19所示的σ光的情况,可 求得: · 01 ·

sino nsin 1.3.14a) {=n 2sin0。 1.3.14b) 并且,因偏光而导致的差异,在临界角附近的低角掠入射情况下,对式1.3.14)影响很 小。这样,反射率 E 和透射率昌都将随0,及Q面变化,在忽略样品吸收的情况 如果8。<9,日成为纯虚数,故反射率后 =1,即发生全反射.当0。=0.时,0= E=1 0 =2,即入射波反射波同位相,折射波的振幅为入射波的2倍。当0。=0时, 层=-1虎=0,入射波与反射波位相相反面相消,襄逝波也酒失。 在考虑到样品对X射线吸收的情汉下,根据式13.10,可求得层随受的变化。 如图1.11所示。综合图1.10和图1.11可以看到,在全反射条件下,对表面、界面的结构分 园缘 员 0特精 图1.11在物质表面处X射线的反射率1EmE。户 随0.0.的变化.0。为掠射角,0.为临界角,AB、CDE 为分别对应B6=0,0.01,0.04,0.08,0.14的曲线m 析以至荧光分析是极为有效的,对来自薄膜衬底的散射可以大大减弱。还可以根据式 1.3.8)和1.3.14)求得 E. E。 随0/0.的变化: h+会h-D过 4.3.15) 其中 ·11·
Em E0 =sinθ0 -nsinθ sinθ0 +nsinθ (1314a) E E0 = 2sinθ0 sinθ0 +nsinθ (1314b) 并且,因偏光而导致的差异,在临界角附近的低角掠入射情况下,对式(1314)影响很 小。这样,反射率 Em E0 2 和透射率 E E0 2 都将随θ0 及θc 而变化。在忽略样品吸收的情况 下,如果θ0 <θc,θ成为纯虚数,故反射率 Em E0 2 =1,即发生全反射。当θ0 =θc 时,θ= 0,Em E0 =1,E E0 =2,即入射波反射波同位相,折射波的振幅为入射波的2倍。当θ0 =0时, Em E0 =-1,E E0 =0,入射波与反射波位相相反而相消,衰逝波也消失。 在考虑到样品对X射线吸收的情况下,根据式(1314),可求得 E E0 2 随θ0 θc 的变化。 如图111所示。综合图110和图111可以看到,在全反射条件下,对表面、界面的结构分 园 员 反 园援缘 射 率 θ燥辕θ糟 月 悦 阅 粤 耘 园援缘 员 员援缘 图111 在物质表面处X射线的反射率|Em/E0|2 随θ0/θc 的变化。θ0 为掠射角,θc 为临界角,A、B、C、D、E 为分别对应β/δ=0,001,004,008,014的曲线[17] 析以至荧光分析是极为有效的,对来自薄膜衬底的散射可以大大减弱。还可以根据式 (138)和(1314)求得 Em E0 2 随θ0?θc 的变化: Em E0 2 = h-θ0 θc 槡2(h-1) 1 2 h+ θ0 θc 槡2(h-1) 1 2 (1315) 其中 · 11 ·

h=(会+√受-1了+(层.在图1.11中曲线ABCD.E是从不考虑吸收以 致吸收越来越大的反射率变化曲线。利用全反射可以对X射线进行聚光或做X射线镜。 1.4X射线的散射和衍射 物质对X射线的散射有相干的称为弹性散射”)和非相干的称为“非弹性散射”)两种。 对于前者,其散射波和入射波具有相同的波长,并且散射前后具有确定的位相关系,散射波之 间相互干涉,产生衍射现象,这为用X射线对物质结构进行分析提供了所需信息。而后者则在 散射过程中随着能量的损失,散射波的波长发生变化,并且位相也无固定关系。 1.4.1弹性散射 当X射线入射到物质上时,物质中的电子便在X射线电场的作用下做加速运动,加速 运动的电子以球面波的形式向周围空间辐射电磁波,即散射波。历史上称这种以电子为散 射体的散射为“Thomson散射”。 如设物质中原子内的电子是“自由”的,则由一个电子所散射的散射波,在距离r处的 强度1,可表示为: = 1.4.1) 式中1。为入射波的强度,r.为经典电子半径(r.=e24πeomc2=2.8179×105[m]),P 为偏振因子,可表示为: P sin'y (1.4.2) X为电子的振动方向与散射波传播方向的夹角。在电子的振动方向(x=0)散射波的强度 为0,在其垂直方向(x=牙)强度最大。 入射 图1.12电子对X射线的散射 实际上原子中的电子是受束缚的。对此,可做如下处理,如图1.12所示,置电子于原 点,取X射线传播方向为z轴,取X射线电场作用下电子受迫振动的方向为x轴,则电子 的运动方程可表示为: ·12·
h= θ0 ( ) θc 2 + θ0 ( ) θc 2 [ ] -1 2 +( )β 槡 δ 2 。在图111中曲线A、B、C、D、E是从不考虑吸收以 致吸收越来越大的反射率变化曲线。利用全反射可以对X射线进行聚光或做X射线镜。 14 X射线的散射和衍射 物质对X射线的散射有相干的(称为“弹性散射”)和非相干的(称为“非弹性散射”)两种。 对于前者,其散射波和入射波具有相同的波长,并且散射前后具有确定的位相关系,散射波之 间相互干涉,产生衍射现象,这为用X射线对物质结构进行分析提供了所需信息。而后者则在 散射过程中随着能量的损失,散射波的波长发生变化,并且位相也无固定关系。 141 弹性散射 当X射线入射到物质上时,物质中的电子便在X射线电场的作用下做加速运动,加速 运动的电子以球面波的形式向周围空间辐射电磁波,即散射波。历史上称这种以电子为散 射体的散射为“Thomson散射”。 如设物质中原子内的电子是“自由”的,则由一个电子所散射的散射波,在距离r处的 强度Ie 可表示为: Ie =I0 Pr2 e r2 (141) 式中I0 为入射波的强度,re 为经典电子半径(re =e2 ?4πε0mc2 =28179×10-15[m]),P 为偏振因子,可表示为: P =sin2 χ (142) χ为电子的振动方向与散射波传播方向的夹角。在电子的振动方向(χ=0)散射波的强度 为0,在其垂直方向(χ = π 2)强度最大。 则 曾 χ 韵 电子 散射波 入射波 匀泽 耘泽 耘燥 扎 图112 电子对X射线的散射 实际上原子中的电子是受束缚的。对此,可做如下处理,如图1.12所示,置电子于原 点,取X射线传播方向为z轴,取X射线电场作用下电子受迫振动的方向为x轴,则电子 的运动方程可表示为: · 21 ·

m()-e 1.4.3) 式中E。“为X射线的电场,x为电子自平衡位置的位移。式(1.4.3)左边第2项为电子 辐射电磁波的阻尼力,Y为阻尼因子,第3项为电子云的束缚力,。为电子的固有振动 (角)频率。式1.4.3)的稳定解为: eEoeh x=m (o w -iro) 1.4.4) 电子的偶极矩P为: -e2Eoe p=-x=mw2-6-i0) 1.4.5) 当电子的振动速度x远比光速小时,则处在原点的电偶极子所辐射的电磁场在充分远的 r处,可表示为: E,(=rx (rxp) 1.4.6) 4πe0cr H,(t)=eor×E,(t) =-r×P 1.4.7) 4πcr2 式中P=-品为时刻:=1一二的值,:叫延迟时间把式1,4.)代入式4.6可 将E,(t)表为: E,)=0-6-i07 -1r×xE)e" 1.4.8) 其中,=rlr,E,、E。分别表示E,和E。的单位矢量,可得: 1E=a@-前+70导16 1.4.9) 这里P=(8,·8)2为偏振因子。设以L,表示散射波的强度,则从式1.4.9)可得: ↓=6ia-3+7月 (1.4.10) 当散射体为自由电子时,上式中的o=0阻尼因子 y=0,散射波的强度还归于式1.4.1),只需将L改 写为L即可。 ,散射波 在图1.13中,把散射线的散射角20与方位角 表示出来,这时偏光因子P就可表示为: P sin2 cos220cos2 (1.4.11) 现在先考虑入射光为线偏振光的情况。当偏振矢量 。与散射面垂直[如图1.14a)]时,散射光的偏振矢 量ε,也与散射面垂直,这时有中=牙,P=1:而当 ,处于散射面内[如图1.146)]时,散射光的E,也 图1,13散射线的散射角与方位角 ·13·
m(d2 x dt2 +γ dx dt +ω0 2 x)=-eE0e iωt (1.4.3) 式中 E0e iωt 为X射线的电场,x为电子自平衡位置的位移。式(143)左边第2项为电子 辐射电磁波的阻尼力,γ 为阻尼因子,第3项为电子云的束缚力,ω0 为电子的固有振动 (角)频率。式(143)的稳定解为: x = eE0e iωt m(ω2 -ω2 0 -iγω) (144) 电子的偶极矩P 为: P =-ex = -e2 E0e iωt m(ω2 -ω2 0 -iγω) (145) 当电子的振动速度x · 远比光速小时,则处在原点的电偶极子所辐射的电磁场在充分远的 r处,可表示为: Es (t)=r×(r×P ) 4πε0c2 r3 (146) Hs (t)=ε0cr×Es (t) r =-r×P ·· 4πcr2 (147) 式中P =-ed2 x dt2 为时刻τ=t-r c 的值,τ叫延迟时间。把式(145)代入式(146)可 将Es (t)表为: Es (t)=re ω2 ω2 -ω2 0 -iγω 1 rr ∧ ×(r ∧ ×E0)e iωt (148) 其中,r ∧ =r?r,εs、ε0 分别表示Es 和E0 的单位矢量,可得: |Es|2 =r2 e ω4 (ω2 -ω2 0)2 +γ2 ω2 P r2|E0|2 (149) 这里P =(εs·ε0)2 为偏振因子。设以Is 表示散射波的强度,则从式(149)可得: Is =I0r2 e ω4 (ω2 -ω2 0)2 +γ2 ω2 P r2 (1410) 圆θ 则 曾 ε园 散射波 入射波 扎 赠 图113 散射线的散射角与方位角 当散射体为自由电子时,上式中的ω0 =0,阻尼因子 γ=0,散射波的强度还归于式(141),只需将Is改 写为Ie 即可。 在图113中,把散射线的散射角2θ与方位角 表示出来,这时偏光因子P 就可表示为: P =sin2 +cos2 2θcos2 (1411) 现在先考虑入射光为线偏振光的情况。当偏振矢量 ε0与散射面垂直[如图114(a)]时,散射光的偏振矢 量εs 也与散射面垂直,这时有= π 2,P =1;而当 ε0 处于散射面内[如图114(b)]时,散射光的εs 也 · 31 ·

在散射面之内,这时÷=0,P=c0s220。对前者称为g光,后者称为π光。 入射波散射面散射波 、泽 图1.14线偏振入射的X射线:)σ光,Nπ光与散射面的关系 在实验室中,由X光管所辐射出的X射线是非偏振的,即。取垂于直传播方向的所 有方向。这时的偏光因子P,可就方位角平均,求出: P=号1+cos220) 1.4.12) X射线的电磁场与电子电荷间的电的互作用产生Thomson散射:而X射线的电磁场 与电子的自旋及其轨道角动量间的磁的互作用,可以产生磁散射。如果入射光很强(如同 步辐射光)也可用磁散射来研究磁性晶体的磁结构,通常磁散射的振幅比Thomson散射 的振幅要小至几个数量级 1.4.2非弹性散射 以上所述,可认为是电子对X射线波的散射。电子还可以与X射线光子相撞而产生散 射。在这一过程中,X射线光子把一部分动量和能量转移给电子,此即所谓Compton散射, 如图1.15所示。具有能量助o的X射线光子经与静止的电子相撞后,能量变为@,根据 能量、动量守恒定律可得: =1+h-os2) 1.4.13) WU. mc 敢射光子 /反神电子, 入射光子 图1.15 Compton散射 式1.4.13)还可表示为: -a=4-20 1.4.14) 其中Ao,入,分别表示散射前后X射线的波长。h/mc=0.00243nm称为Compton波长。由 式1.4.14)可知散射角20越大,波长的变化越大,向后散射越显著。根据相对论量子力学 的处理,非偏振的X射线Compton散射的微分截面为: d=号g+-m0an .4.15) ·14·
在散射面之内,这时=0,P =cos2 2θ。对前者称为σ光,后者称为π光。 ε园 圆θ ε泽 圆θ 穴葬雪 泽园 入射波 散射面 散射波 穴遭雪 ε园 ε泽 泽 图114 线偏振入射的X射线:(a)σ光,(b)π光与散射面的关系 在实验室中,由X光管所辐射出的X射线是非偏振的,即ε0 取垂于直传播方向的所 有方向。这时的偏光因子P,可就方位角平均,求出: P = 1 2 (1+cos2 2θ) (1412) X射线的电磁场与电子电荷间的电的互作用产生Thomson散射;而X射线的电磁场 与电子的自旋及其轨道角动量间的磁的互作用,可以产生磁散射。如果入射光很强(如同 步辐射光)也可用磁散射来研究磁性晶体的磁结构,通常磁散射的振幅比 Thomson散射 的振幅要小至几个数量级。 142 非弹性散射 以上所述,可认为是电子对X射线波的散射。电子还可以与X射线光子相撞而产生散 射。在这一过程中,X射线光子把一部分动量和能量转移给电子,此即所谓Compton散射, 如图1.15所示。具有能量ω0 的X射线光子经与静止的电子相撞后,能量变为ωs,根据 能量、动量守恒定律可得: ω0 ωs =1+ ω0 mc2(1-cos2θ) (1413) 入射光子 散射光子 反冲电子 圆θ 图115 Compton散射 式(1413)还可表示为: λs -λ0 = h mc (1-cos2θ) (1414) 其中λ0,λs 分别表示散射前后X射线的波长。h?mc=000243nm称为Compton波长。由 式(1414)可知散射角2θ越大,波长的变化越大,向后散射越显著。根据相对论量子力学 的处理,非偏振的X射线Compton散射的微分截面为: dσc =r2 e 2 ω2 s ω2 0 (ω0 ωs +ωs ω0 -sin2θ)dΩ (1415) · 41 ·