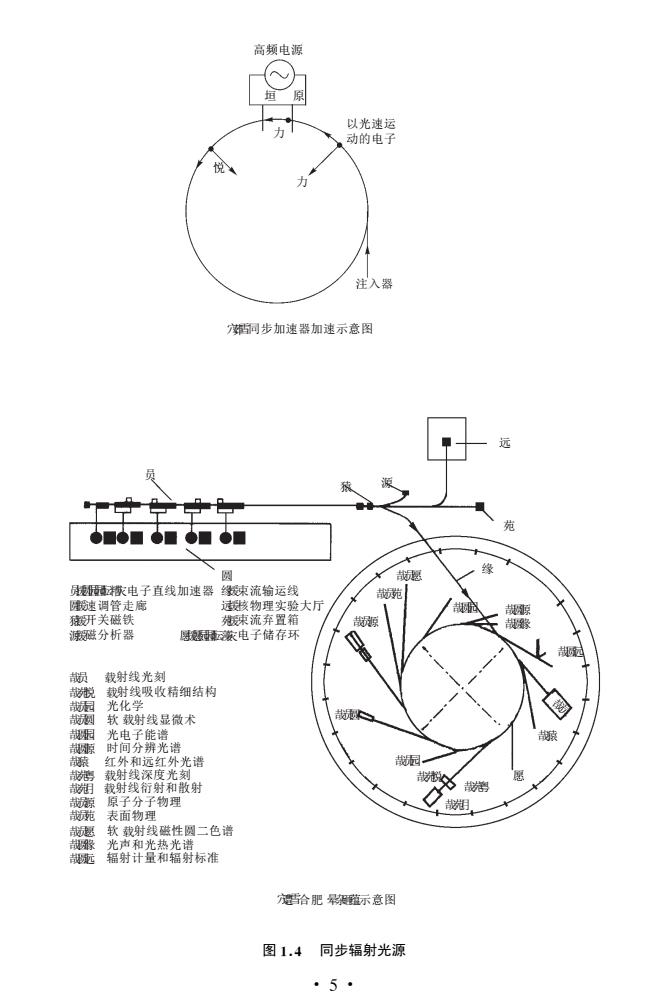
注入器 街可步加速器加速示意图 ●■●■●■●■●■ 歡电子直线加速器 餐流始运线 速调管走廊 速物理实验大厅 载射线光刻 线吸收精细结构 软我射线显微术 光调 射线衍射和敢射 子分子物理 射线磁性圆二色曾 光和射标准 雪合肥架磁示意图 图1.4同步辐射光源 ·5
哉员 哉猿 哉苑粤 哉苑月 哉员园 哉苑悦 愿 哉员圆 哉员 载射线光刻 哉员苑 表面物理 穴葬雪同步加速器加速示意图 员援圆园园酝糟灾电子直线加速器 哉圆远 辐射计量和辐射标准 哉圆缘 光声和光热光谱 哉员源 原子分子物理 哉员愿 软 载射线磁性圆二色谱 哉苑悦 载射线吸收精细结构 哉猿 红外和远红外光谱 哉苑月 载射线衍射和散射 哉苑粤 载射线深度光刻 哉圆源 时间分辨光谱 哉圆园 光电子能谱 哉员圆 软 载射线显微术 哉员园 光化学 愿援愿园园酝藻灾电子储存环 远援核物理实验大厅 苑援束流弃置箱 缘援束流输运线 源援磁分析器 猿援开关磁铁 圆援速调管走廊 哉员源 圆 员 猿 垣 原 高频电源 悦 力 力 哉圆园 穴遭雪合肥 晕杂砸蕴示意图 哉圆缘 哉圆源 缘 哉员苑 哉圆远 哉员愿 远 苑 源 注入器 以光速运 动的电子 图14 同步辐射光源 ·5·
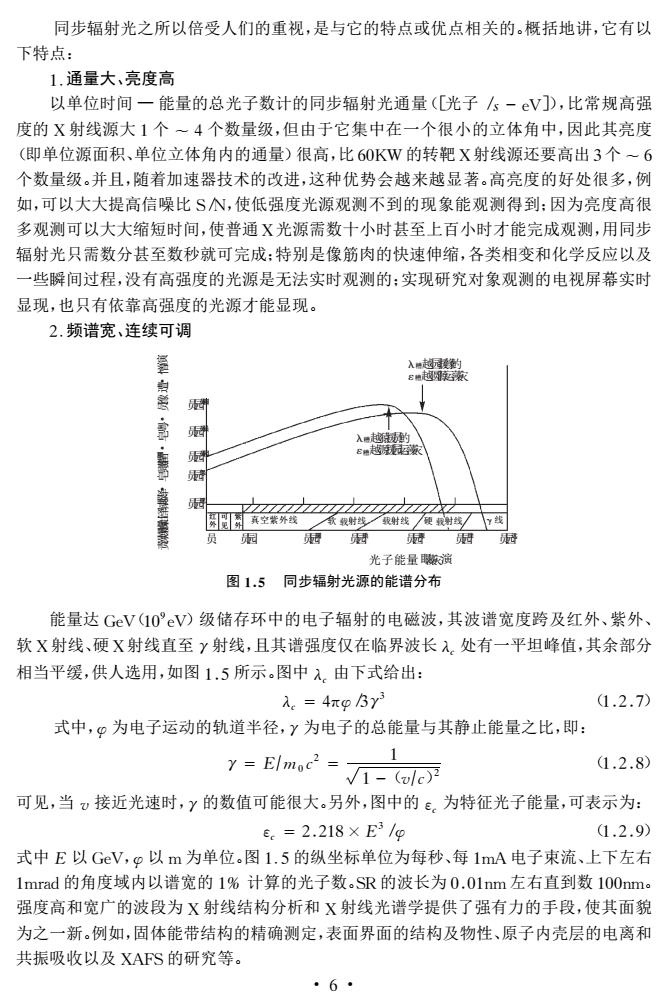
同步辐射光之所以倍受人们的重视,是与它的特点或优点相关的。概括地讲,它有以 下特点: 1.通量大、亮度高 以单位时间一能量的总光子数计的同步辐射光通量([光子s-eV]),比常规高强 度的X射线源大1个一4个数量级,但由于它集中在一个很小的立体角中,因此其亮度 (即单位源面积、单位立体角内的通量)很高,比60KW的转靶X射线源还要高出3个一6 个数量级。并且,随着加速器技术的改进,这种优势会越来越显著。高亮度的好处很多,例 如,可以大大提高信噪比SN,使低强度光源观测不到的现象能观测得到:因为亮度高很 多观测可以大大缩短时间,使普通X光源需数十小时甚至上百小时才能完成观测,用同步 辐射光只需数分甚至数秒就可完成:特别是像筋肉的快速伸缩,各类相变和化学反应以及 一些瞬间过程,没有高强度的光源是无法实时观测的:实现研究对象观测的电视屏幕实时 显现,也只有依靠高强度的光源才能显现。 2.频谱宽、连续可调 入 真空装外 员 光子能量演 图1.5同步辐射光源的能谱分布 能量达GeV(10'©V)级储存环中的电子辐射的电磁波,其波谱宽度跨及红外、紫外 软X射线、硬X射线直至Y射线,且其谱强度仅在临界波长入处有一平坦峰值,其余部分 相当平缓,供人选用,如图1.5所示。图中入,由下式给出: 入=4π9By 1.2.7) 式中,9为电子运动的轨道半径,y为电子的总能量与其静止能量之比,即: y=Elmoc2 1 1.2.8) √1-(olc) 可见,当0接近光速时,y的数值可能很大。另外,图中的。为特征光子能量,可表示为: e.=2.218×E31e 1.2.9 式中E以GeV,p以m为单位.图1.5的纵坐标单位为每秒、每1mA电子束流、上下左右 1mrad的角度域内以谱宽的1%计算的光子数。SR的波长为0.0lnm左右直到数100nm。 强度高和宽广的波段为X射线结构分析和X射线光谱学提供了强有力的手段,使其面貌 为之一新。例如,固体能带结构的精确测定,表面界面的结构及物性、原子内壳层的电离和 共振吸收以及XAFS的研究等。 6·
同步辐射光之所以倍受人们的重视,是与它的特点或优点相关的。概括地讲,它有以 下特点: 1.通量大、亮度高 以单位时间 — 能量的总光子数计的同步辐射光通量([光子 /s-eV]),比常规高强 度的X射线源大1个 ~4个数量级,但由于它集中在一个很小的立体角中,因此其亮度 (即单位源面积、单位立体角内的通量)很高,比60KW的转靶X射线源还要高出3个 ~6 个数量级。并且,随着加速器技术的改进,这种优势会越来越显著。高亮度的好处很多,例 如,可以大大提高信噪比S/N,使低强度光源观测不到的现象能观测得到;因为亮度高很 多观测可以大大缩短时间,使普通X光源需数十小时甚至上百小时才能完成观测,用同步 辐射光只需数分甚至数秒就可完成;特别是像筋肉的快速伸缩,各类相变和化学反应以及 一些瞬间过程,没有高强度的光源是无法实时观测的;实现研究对象观测的电视屏幕实时 显现,也只有依靠高强度的光源才能显现。 2.频谱宽、连续可调 责澡燥贼燥灶泽辕眼·泽 皂 圆 则葬凿·皂粤·员豫 遭·憎演 硬 载射线 γ 线 员园缘 员园远 光子能量眼藻灾演 ε糟越圆源运藻灾 λ糟越园援缘魡 ε糟越源援园运藻灾 λ糟越猿援员魡 员园怨 员园员园 员园愿 员园员员 员园员圆 可 见 红 外 紫 外 员 员园 真空紫外线 软 载射线 员园猿 载射线 员园圆 员园源 图15 同步辐射光源的能谱分布 能量达GeV(109 eV)级储存环中的电子辐射的电磁波,其波谱宽度跨及红外、紫外、 软X射线、硬X射线直至γ射线,且其谱强度仅在临界波长λc处有一平坦峰值,其余部分 相当平缓,供人选用,如图15所示。图中λc 由下式给出: λc =4πφ/3γ3 (127) 式中,φ为电子运动的轨道半径,γ为电子的总能量与其静止能量之比,即: γ =E?m0c2 = 1 槡1-(v?c)2 (128) 可见,当v接近光速时,γ的数值可能很大。另外,图中的εc 为特征光子能量,可表示为: εc =2218×E3/φ (129) 式中E 以GeV,φ以 m为单位。图1.5的纵坐标单位为每秒、每1mA电子束流、上下左右 1mrad的角度域内以谱宽的1% 计算的光子数。SR的波长为001nm左右直到数100nm。 强度高和宽广的波段为X射线结构分析和X射线光谱学提供了强有力的手段,使其面貌 为之一新。例如,固体能带结构的精确测定,表面界面的结构及物性、原子内壳层的电离和 共振吸收以及XAFS的研究等。 ·6·
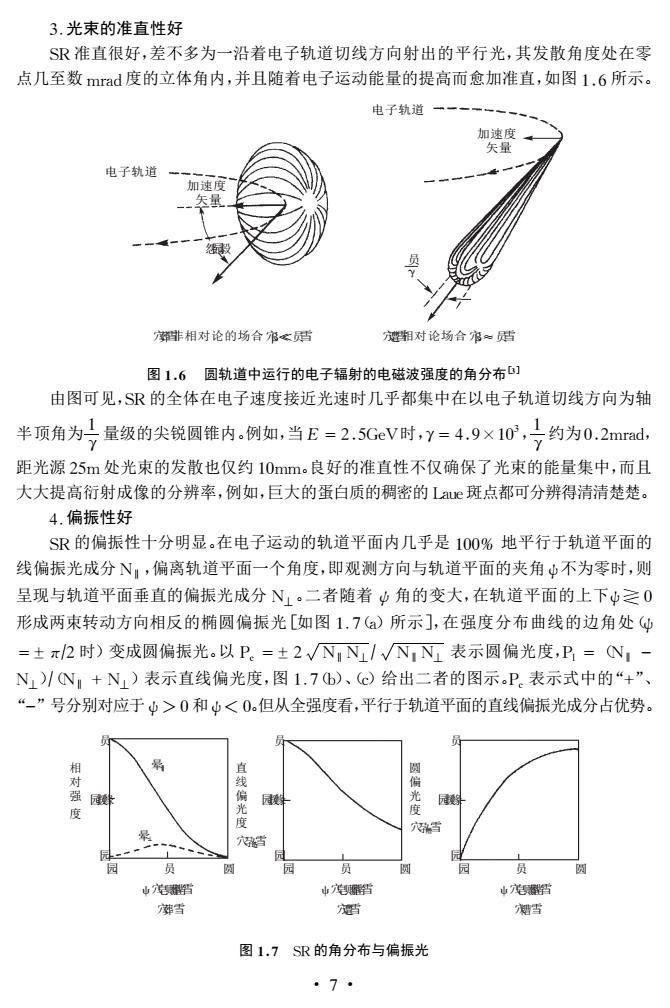
3.光束的准直性好 SR准直很好,差不多为一沿着电子轨道切线方向射出的平行光,其发散角度处在零 点几至数mrad度的立体角内,并且随着电子运动能量的提高而愈加准直,如图1.6所示。 电子轨道 电子轨道 相对论的场合窄。站 通塑对论场合窄。猫 图1.6圆轨道中运行的电子辐射的电磁波强度的角分布) 由图可见,SR的全体在电子速度接近光速时几乎都集中在以电子轨道切线方向为轴 半顶角为号量级的尖锐圆锥内。例如,当E=2.5GeV时,Y=4.9×102,号约为0.2mrad, 距光源25m处光束的发散也仅约10m。良好的准直性不仅确保了光束的能量集中,而且 大大提高衍射成像的分辨率,例如,巨大的蛋白质的稠密的Lau斑点都可分辨得清清楚楚。 4.偏振性好 SR的偏振性十分明显。在电子运动的轨道平面内几乎是100%地平行于轨道平面的 线偏振光成分N,,偏离轨道平面一个角度,即观测方向与轨道平面的夹角中不为零时,则 呈现与轨道平面垂直的偏振光成分N1。二者随着角的变大,在轨道平面的上下中之0 形成两束转动方向相反的椭圆偏振光[如图1.7)所示],在强度分布曲线的边角处中 =±π2时)变成圆偏振光。以P。=±2√NN可/√N,N可表示圆偏光度,D=N, N)/N,+N1)表示直线偏光度,图1.7b)、⊙给出二者的图示P表示式中的“+”、 “-”号分别对应于山>0和少<0。但从全强度看,平行于轨道平面的直线偏振光成分占优势。 山 中暂 ·龙芦 图1.7SR的角分布与偏振光 。7
3.光束的准直性好 SR准直很好,差不多为一沿着电子轨道切线方向射出的平行光,其发散角度处在零 点几至数 mrad度的立体角内,并且随着电子运动能量的提高而愈加准直,如图16所示。 γ 员 加速度 矢量 穴葬雪非相对论的场合穴β员雪 穴遭雪相对论场合穴β≈员雪 怨园毅 加速度 矢量 电子轨道 电子轨道 图16 圆轨道中运行的电子辐射的电磁波强度的角分布[3] 由图可见,SR的全体在电子速度接近光速时几乎都集中在以电子轨道切线方向为轴 半顶角为1 γ量级的尖锐圆锥内。例如,当E=25GeV时,γ=49×103,1 γ约为02mrad, 距光源25m处光束的发散也仅约10mm。良好的准直性不仅确保了光束的能量集中,而且 大大提高衍射成像的分辨率,例如,巨大的蛋白质的稠密的Laue斑点都可分辨得清清楚楚。 4.偏振性好 SR的偏振性十分明显。在电子运动的轨道平面内几乎是100% 地平行于轨道平面的 线偏振光成分N‖,偏离轨道平面一个角度,即观测方向与轨道平面的夹角ψ不为零时,则 呈现与轨道平面垂直的偏振光成分 N⊥。二者随着ψ角的变大,在轨道平面的上下ψ0 形成两束转动方向相反的椭圆偏振光[如图1.7(a)所示],在强度分布曲线的边角处(ψ =±π?2时)变成圆偏振光。以Pc =±2 N槡 ‖N⊥?槡N‖N⊥ 表示圆偏光度,Pl =(N‖ - N⊥)?(N‖ +N⊥)表示直线偏光度,图1.7(b)、(c)给出二者的图示。Pc 表示式中的“+”、 “-”号分别对应于ψ>0和ψ<0。但从全强度看,平行于轨道平面的直线偏振光成分占优势。 圆 偏 光 度 穴孕糟雪 员 晕‖ 晕⊥ 园援缘 园 相 对 强 度 ψ穴皂则葬凿雪 穴葬雪 园 员 直 线 偏 光 度 穴孕造雪 员 园援缘 园 圆 园 穴遭雪 穴糟雪 ψ穴皂则葬凿雪 ψ穴皂则葬凿雪 园 员 园援缘 员 圆 园 员 圆 图17 SR的角分布与偏振光 ·7·

偏光对于电子态的研究,对原子、分子电离时光电子角分布情况的研究,对与光电离 有关的初态与终态的对称性及轨道杂化的研究,对固体的能带结构、固体表面的重构、吸 附、脱吸附以及与磁量子数有关的电子跃迁的研究,都具有重要意义。 5.具有特定的时间结构 SR是脉冲光源,由加速器或储存环中相隔一定距离的电子(或其他荷电粒子)束团以 很窄的脉宽和时间间隔辐射出来,这些都可由加速器的设计参数决定。图1.8给出SR的 电场E()随着时间的变化,图中·为电子运动的轨道半径。脉冲光源对原子、分子激发态 寿命的测定,光化学反应的时间常数的测定以及许多瞬时过程的研究都很有意义。 图1.8SR电场随时间的变化 6.光谱纯洁无污染 S的发光机制决定它是纯洁的,不像通常的X光管那样既有特征辐射又有因管中其 他粒子或靶物质上沉积其他物质等导致的杂散辐射,给其后的利用和分析带来不便。 此外,S的特性可从理论上进行计算,非插入件辐射的光无相干性,而插入件辐射的 光带部分相干性等特点。 1.3X射线的折射和全反射 X射线传播至两种介质的界面处时,即发生折射和反射。 1.3.1折射 现考虑X射线从真空入射到一种物质上,设在真空中其波矢大小为K,在物质中其波 矢大小为k,则其在该物质中的折射率n为: n =kK (1.3.1) 与可见光不同,X射线的折射率n<1,设物质与真空的介电常数和磁导率分别为e、。和 4小,则折射率n也可表示为: n二入e0o /E4 1.3.2) 对于普通的物质,可以认为4=因此,式1.3.2)变为: n=VElEo 1.3.3) e与物质的平均极化率X。具有如下关系: ·8
偏光对于电子态的研究,对原子、分子电离时光电子角分布情况的研究,对与光电离 有关的初态与终态的对称性及轨道杂化的研究,对固体的能带结构、固体表面的重构、吸 附、脱吸附以及与磁量子数有关的电子跃迁的研究,都具有重要意义。 5.具有特定的时间结构 SR是脉冲光源,由加速器或储存环中相隔一定距离的电子(或其他荷电粒子)束团以 很窄的脉宽和时间间隔辐射出来,这些都可由加速器的设计参数决定。图18给出SR的 电场E(t)随着时间的变化,图中ψ为电子运动的轨道半径。脉冲光源对原子、分子激发态 寿命的测定,光化学反应的时间常数的测定以及许多瞬时过程的研究都很有意义。 圆πψ 糟 耘穴贼雪 糟则猿 ψ 贼 图18 SR电场随时间的变化 6.光谱纯洁无污染 SR的发光机制决定它是纯洁的,不像通常的X光管那样既有特征辐射又有因管中其 他粒子或靶物质上沉积其他物质等导致的杂散辐射,给其后的利用和分析带来不便。 此外,SR的特性可从理论上进行计算,非插入件辐射的光无相干性,而插入件辐射的 光带部分相干性等特点。 1.3 X射线的折射和全反射 X射线传播至两种介质的界面处时,即发生折射和反射。 1.3.1 折射 现考虑X射线从真空入射到一种物质上,设在真空中其波矢大小为K,在物质中其波 矢大小为k,则其在该物质中的折射率n为: n =k?K (1.3.1) 与可见光不同,X射线的折射率n<1,设物质与真空的介电常数和磁导率分别为ε、ε0和 μ、μ0,则折射率n也可表示为: n = εμ 槡ε0μ0 (132) 对于普通的物质,可以认为μ=μ0。因此,式(132)变为: n = 槡ε/ε0 (133) ε与物质的平均极化率χ0 具有如下关系: ·8·

e=eo1+X。) (1.3.4) 而X。又由下式给出: Xo=-A're Fo h v 1.3.5) 式中,入为波长,r。是经典电子半径,0.为物质的晶胞体积,Fo为物质对X射线的散射角 20=0时的结构因数。如果计及以后将要讲到的原子的异常散射项了和”,则 Fo=∑%,+了,+f,) 1.3.6) 乙为晶胞中原子j的原子序数,N为晶胞中的原子数。综合式1.3.3)一1.3.5),可将n 表示为: n=1-λ2r.Fo2πu 1.3.7) 式1.3.7)可进一步表示为: n=1-8+3 1.3.8) a-0空g+p=空刀 若令了=0,则: 1.3.9) 式中N一是头为物质单位体积中的电于致当物质为单质时,=心ZM,这里 Na为Avogadro常数,Z为原子序数,M为原子量,p是密度。一般情况下,6仅为10-5~ 106数量级,B对应于X射线的吸收。可见,对X射线不可能像通常的光学情况那样制作 透镜和棱镜。 1.3.2全反射 由于物质对X射线的折射率比1小,所以当其以低于临界角(,的角度掠入射到固体、 液体等物质的表面时,就会发生全反射。设X射线对某物质的临界角为日.(这里所取的临 界角与通常光学中的临界角互余),则当忽略物质的吸收时,根据snl定律有: sin(5-0.)sin号=1-d 1.3.10) 进而可近似求得: 0=√2d (1.3.11a 或具体化为: 0.[mrad]=2.99×l0-4√NE Lm[nm] (1.3.11b) X射线的波长愈大,构成物质的原子序数愈大,即单位体积中的电子数愈多,日。也愈大。 ·9·
ε=ε0 (1+χ0 ) (134) 而χ0 又由下式给出: χ0 =-λ2 reFo/πvc (135) 式中,λ为波长,re 是经典电子半径,vc 为物质的晶胞体积,Fo为物质对X射线的散射角 2θ=0时的结构因数。如果计及以后将要讲到的原子的异常散射项f′和if″,则 Fo= ∑ N j (Zj +f′j +if″j) (136) Zj 为晶胞中原子j的原子序数,N 为晶胞中的原子数。综合式(133)~(135),可将n 表示为: n =1-λ2reF0/2πvc (137) 式(137)可进一步表示为: n =1-δ+iβ (138) 其中,δ=λ2 re 2πvc ∑ N j (Zj +f′j), β=λ2 re 2πvc∑ N j (-f″j) 若令f′=0,则: δ=λ2 re 2π NE (139) 式中NE = 1 vc ∑ N j Zj为物质单位体积中的电子数。当物质为单质时,NE =NAZρ?M,这里 NA 为Avogadro常数,Z 为原子序数,M 为原子量,ρ是密度。一般情况下,δ仅为10-5 ~ 10-6 数量级,β对应于X射线的吸收。可见,对X射线不可能像通常的光学情况那样制作 透镜和棱镜。 132 全反射 由于物质对X射线的折射率比1小,所以当其以低于临界角θc的角度掠入射到固体、 液体等物质的表面时,就会发生全反射。设X射线对某物质的临界角为θc (这里所取的临 界角与通常光学中的临界角互余),则当忽略物质的吸收时,根据snell定律有: sin(π 2-θc)/sinπ 2 =1-δ (1310) 进而可近似求得: θc = 槡2δ (1311a) 或具体化为: θc [mrad]=299×10-14 NE [m-3 槡 ]λ[nm] (1311b) X射线的波长愈大,构成物质的原子序数愈大,即单位体积中的电子数愈多,θc 也愈大。 ·9·