5.2边缘检测 1边缘检测原理 其导数在边缘方向取得极值 (b)每行像素的 灰度剖面图 (a)一幅纵向 (c)一阶导数 边缘的图像 (d)二阶导数 从数学上看,图像的模糊相当于图像被平均或积分,为实现图象的 锐化,必需用它的反运算“微分”一一加强高频分量作用,使轮廓清晰。 教字图像处要 ■■■
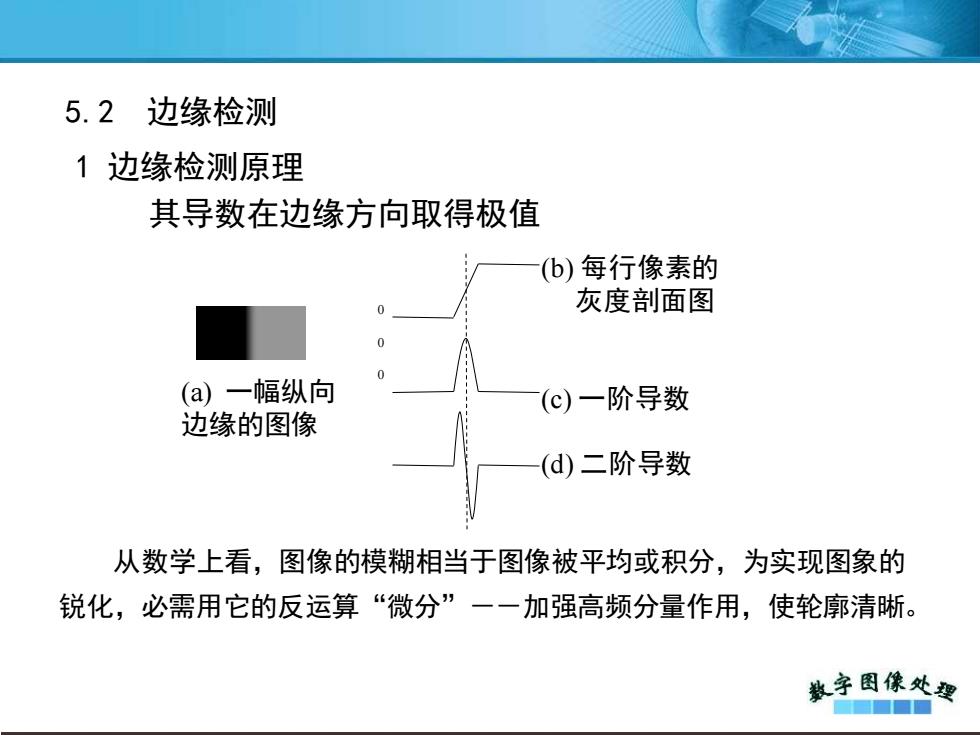
(a) 一幅纵向 边缘的图像 0 0 0 (b) 每行像素的 灰度剖面图 (c) 一阶导数 (d) 二阶导数 从数学上看,图像的模糊相当于图像被平均或积分,为实现图象的 锐化,必需用它的反运算“微分”--加强高频分量作用,使轮廓清晰。 5.2 边缘检测 1 边缘检测原理 其导数在边缘方向取得极值

1边缘检测原理 梯度对应一阶导数,对于一个连续图像函数f(x,y): 梯度矢量定义:x-6,G[高] 梯度的幅度:f(x,y)=mag(Vfx,y》=(G+G)2 梯度的方向:(x,y)=arctan(G,/Gx) 教字图像处要 ■■■■
梯度对应一阶导数,对于一个连续图像函数f(x,y): T T x y y f x f f x y G G ( , ) = = 2 2 1 2 ( , ) ( ( , )) ( ) Gx Gy f x y = mag f x y = + ( , ) arctan( ) Gy Gx x y = 梯度的幅度: 梯度矢量定义: 梯度的方向: 1 边缘检测原理

1边缘检测原理 离散域上微分改成差分,而且由水平和垂直两个 方向模板组成 一阶: Ax f(ij)=f(ij)-f(i,j-1) Ay f(i,j)=f(ij)-f(i-1,j) 二阶:△x2fi,j)=△xfij+l)-△xfj) =f(ij+1)-f(i,j)-(f(ij)f(ij-1)) Ay2f(i,i)=f(i+1,i)+f(i-1,i)-2f(i,i) 教字图像处要 ■■■
离散域上微分改成差分,而且由水平和垂直两个 方向模板组成 一阶: △x f(i,j) = f(i,j) - f(i,j-1) △y f(i,j) = f(i,j) - f(i-1,j) 二阶:△x 2 f(i,j) = △x f(i,j+1) - △x f(i,j) = f(i,j+1) - f(i,j) –( f(i,j) - f(i,j-1)) △y 2 f(i,j) = f(i+1,j) + f(i-1,j) - 2f(i,j) 1 边缘检测原理

2典型算子 a)Roberts.算子 8,小=f6)-f+1j+明+t+1,办-f,j+f 近似式: fi,)-f(i+1,广+1+f(i+1,)-f(i,j+1) 1 01 -10 Roberts?算子 数字图像处要 ■■■■
a) Roberts算子 ( ) ( ) ( ) ( ) ( ) 2 1 2 2 g i, j = f i, j − f i +1, j +1 + f i +1, j − f i, j +1 近似式: 1 0 0 -1 0 1 -1 0 Roberts算子 2 典型算子 f (i, j) − f (i +1, j +1) + f (i +1, j) − f (i, j +1)
2典型算子 b)Sobel算子 -1 1 2 1 -2 0 0 0 -1 -2 -1 c)Prewitt算子 -1 0 -1 0 -1 0 教字图像处要 ■■■
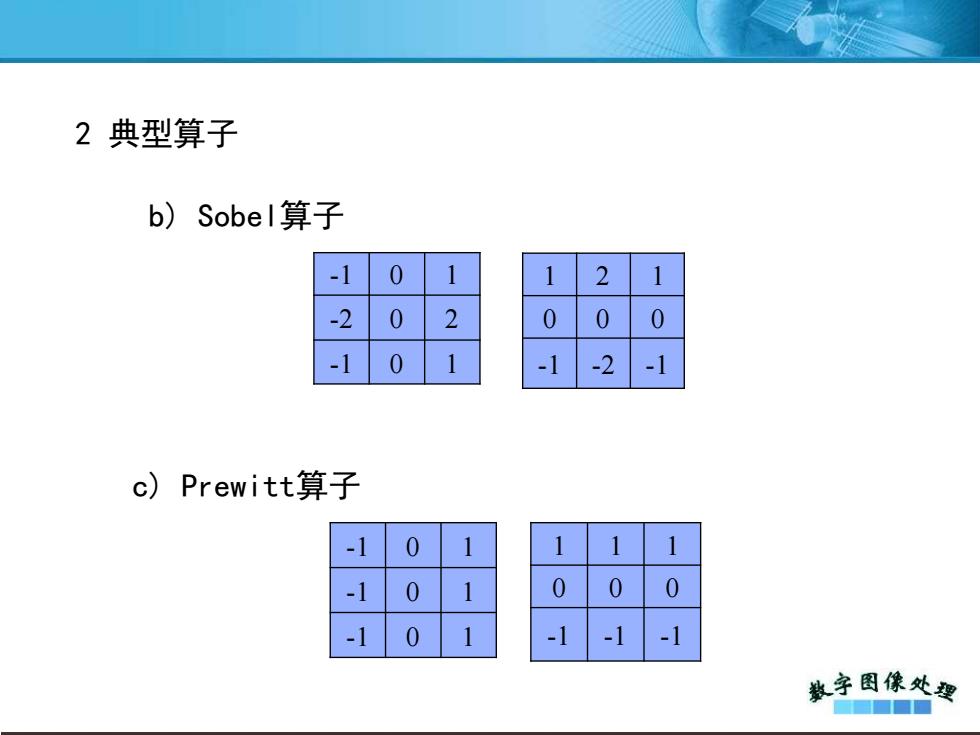
b) Sobel算子 -1 0 1 -2 0 2 -1 0 1 1 2 1 0 0 0 -1 -2 -1 c) Prewitt算子 -1 0 1 -1 0 1 -1 0 1 1 1 1 0 0 0 -1 -1 -1 2 典型算子