南京大学：《高级优化 Advanced Optimization》课程教学资源（讲稿）Lecture 02 Convex Optimization Basics; Function Properties

Convex Function Examples on R: Exponential:ea,where a ER. -Powers::za,where a≥1ora≤0. Powers of absolute value:P,where p >1. Negative logarithm:-logx. Negative entropy:xlogz. Advanced Optimization(Fall 2023) Lecture 2.Convex Optimization Basics 16

Advanced Optimization (Fall 2023) Lecture 2. Convex Optimization Basics 16 Convex Function

Convex Function Examples on Rd: -norm:f(x)=x‖. maximum:f(x)=max {x1,...,n}. Log-sum-exp:f(x)=log (e21+...+e2m). Advanced Optimization(Fall 2023) Lecture 2.Convex Optimization Basics 17

Advanced Optimization (Fall 2023) Lecture 2. Convex Optimization Basics 17 Convex Function

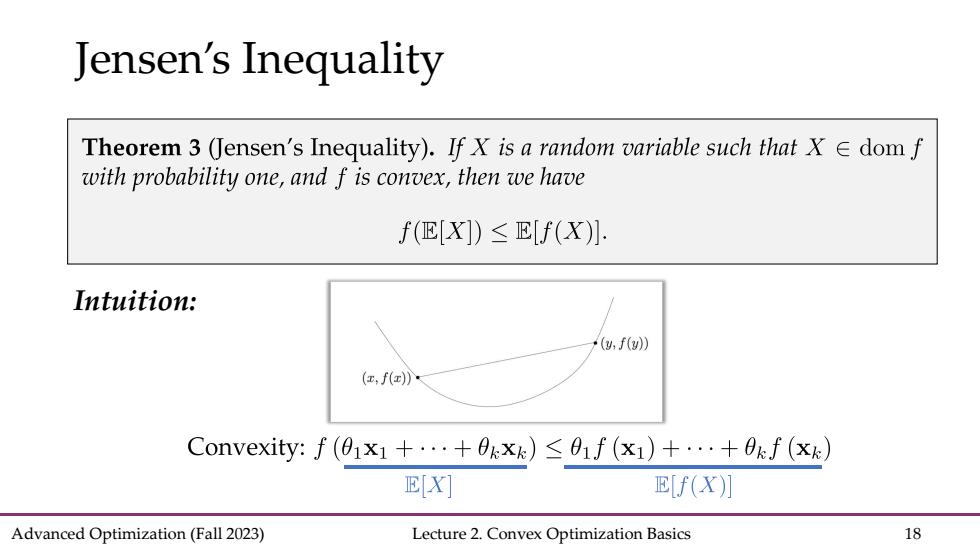
Jensen's Inequality Theorem 3 (Jensen's Inequality).If X is a random variable such that X dom f with probability one,and f is convex,then we have f(E[X])≤E[f(X)]. Intuition: (,f() (,f() Convexity:f(01x1+…+0xk)≤01f(x1）+·+0f(xk) EX E[f(X)] Advanced Optimization(Fall 2023) Lecture 2.Convex Optimization Basics 18

Advanced Optimization (Fall 2023) Lecture 2. Convex Optimization Basics 18 Jensen’s Inequality Intuition:

Part 2.Convex Optimization Problem ·Problem ·Subgradients Why Convexity? Advanced Optimization(Fall 2023) Lecture 2.Convex Optimization Basics 19

Advanced Optimization (Fall 2023) Lecture 2. Convex Optimization Basics 19 Part 2. Convex Optimization Problem • Problem • Subgradients • Why Convexity?

Convex Optimization Problem We adopt a minimization language min f(x) s.t.g(x)≤0，i=1,·,m ax=b,i=1,…,n optimization variable x Rd -convex objective function:f:RdR convex inequality constraints:g1,...,gm Advanced Optimization(Fall 2023) Lecture 2.Convex Optimization Basics 20

Advanced Optimization (Fall 2023) Lecture 2. Convex Optimization Basics 20 Convex Optimization Problem • We adopt a minimization language