
第五章几何对象与变换 酒中国斜学术大室 University of Science and Technology of China 5.1几何 5.2表示 5.3变换
第五章 几何对象与变换 5.1 几何 5.2 表示 5.3 变换 2

5.1几何 中国斜草技术大学 University of Science and Technology of Chin ·与坐标无关的几何 ·仿射空间 一标量 一向量 一点 ·基本几何图元 一线段 一多边形
5.1 几何 • 与坐标无关的几何 • 仿射空间 – 标量 – 向量 – 点 • 基本几何图元 – 线段 – 多边形 3

基本几何要素 中国学我术大草 University of Science and Technology of China ·几何研究n维空间中对象之间的关系 一在计算机图形学中,我们对三维空间中的对象 感兴趣 ·希望得到一个几何形状的最小集合,根据 这个集合可以建立起更复杂的对象 ·需要三个基本元素 一标量 一向量 一点
基本几何要素 • 几何研究n维空间中对象之间的关系 – 在计算机图形学中,我们对三维空间中的对象 感兴趣 • 希望得到一个几何形状的最小集合,根据 这个集合可以建立起更复杂的对象 • 需要三个基本元素 – 标量 – 向量 – 点 4
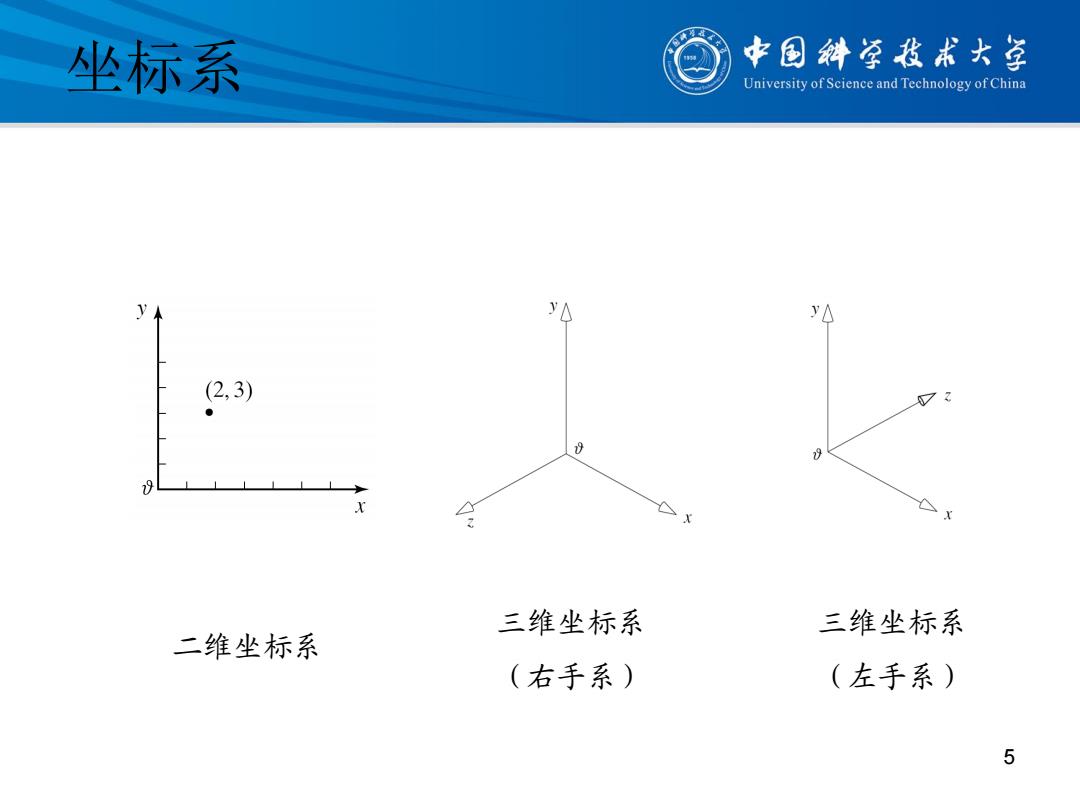
坐标系 中国斜草我术大草 University of Science and Technology of China .3 三维坐标系 三维坐标系 二维坐标系 (右手系) (左手系)
坐标系 5 二维坐标系 三维坐标系 (右手系) 三维坐标系 (左手系)

与坐标无关的几何 中国斜学我术大草 University of Scie ·在初等解析几何中,主要应用的是直角坐 标系(笛卡尔坐标系) -点在空间中的位置是p=(仪,y,z) 一通过对这些坐标进行代数运算导出结果 ·这种方法不是基于物理的 一从物理的角度来讲,点的存在性是与坐标系的 具体位置无关的 一绝大多数几何结果是不依赖于坐标系的 一例如,在欧氏几何中,两个三角形全等是指它 们有两个对应边和夹角相等
与坐标无关的几何 • 在初等解析几何中,主要应用的是直角坐 标系(笛卡尔坐标系) – 点在空间中的位置是p = (x,y,z) – 通过对这些坐标进行代数运算导出结果 • 这种方法不是基于物理的 – 从物理的角度来讲,点的存在性是与坐标系的 具体位置无关的 – 绝大多数几何结果是不依赖于坐标系的 – 例如,在欧氏几何中,两个三角形全等是指它 们有两个对应边和夹角相等 6