上海交通大学：《材料加工原理 Principles of Materials Processing》教学资源（课程讲稿）04. Technology of plasticity——plastic deformation mechanism

Elastic properties of dislocation 国上清充通大￥ SHEAMGRAI DUD TONO UHTVEREETTY Stress field of edge dislocation The elastic field inIn Cartesian coordinate system The strain in z-direction is zero. √Plane strain Gb y(3x2+y2) y 0xx=- 2π(1-0)(x2+y22 Gby(x2-y2) 0y=2π1-0)(x2+y2)2 :=U(oxx+oyy) Gb x(x2-y2) tw=tx=2π0-0)(x2+y2)2 Institute of Forming Technology Equipment 12

Elastic properties of dislocation Institute of Forming Technology & Equipment 12 Stress field of edge dislocation x y z b P 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 1 ( ) 2 (1 ) ( ) ( ) ( ) 2 (1 ) ( ) x x y y zz xx yy xy yx Gb y( x y ) σ π ( υ ) (x y ) Gb y x y x y Gb x x y x y                             zz yx yy xx xy      0 0 00  The elastic field in In Cartesian coordinate system  The strain in z‐direction is zero.  Plane strain

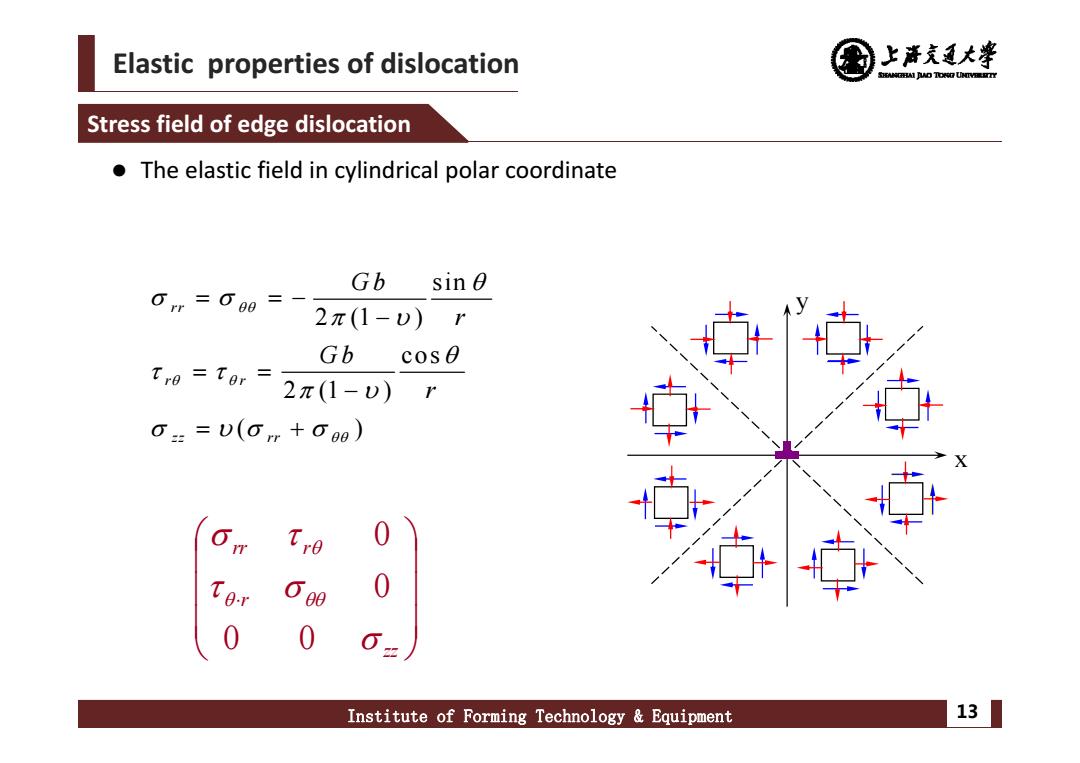
Elastic properties of dislocation 上清充通大孝 SANCEAI JUO TO阳UY Stress field of edge dislocation The elastic field in cylindrical polar coordinate Gb sinθ Or=O阳= 2π(1-D)r Gb cos0 Tro Tor= 2π(1-v）r 0==D(Om+0g) Institute of Forming Technology Equipment 13

Elastic properties of dislocation Institute of Forming Technology & Equipment 13  The elastic field in cylindrical polar coordinate Stress field of edge dislocation sin 2 (1 ) cos 2 (1 ) ( ) rr r r zz rr G b r G b r                             zz rrr r         0 0 00 y x

Elastic properties of dislocation 上产克大睾 SHANCBHAI JUAO TONO UNTVEEETTY Stress field of mixed dislocation The elastic field of a mixed dislocation: having edge and screw character adding the fields of the edge and screw constituents The stress components for edge and screw dislocation elastic field are independent of each other. b XX b。=bsin0 O b,=b·cos0 Institute of Forming Technology Equipment 14

Elastic properties of dislocation Institute of Forming Technology & Equipment 14  The elastic field of a mixed dislocation:  having edge and screw character  adding the fields of the edge and screw constituents  The stress components for edge and screw dislocation elastic field are independent of each other. Stress field of mixed dislocation be  bsin bs  b  cos  b    be θ  bs xz  yz  zx  zy  zz  yy  yx  xy  xx   

Elastic properties of dislocation 上清充通大学 SHEAMGRAI DUD TONO UHTVEREETTY Strain energy of screw dislocation 口 The presence of a dislocation costs energy to the crystal.So,dislocations have distortion energy. The energy is expressed as Energy per unit length of dislocation line →Units:[J/m] ▣，Edge→Compressive and tensile stress fields Screw-Shear stress fields The energy of a dislocation:approximately from linear elastic theory.Near the dislocation line the distortions are very large and the linear elastic description fails in this region called the Core of the dislocation (this region range from b to 5b).The energy of the core is about 1/10 the total energy of the dislocation. Elastic Energy of dislocation Non-elastic(Core) ~E/10 Institute of Forming Technology Equipment 15

Elastic properties of dislocation Institute of Forming Technology & Equipment 15 Strain energy of screw dislocation  The presence of a dislocation costs energy to the crystal. So, dislocations have distortion energy.  The energy is expressed as Energy per unit length of dislocation line → Units: [J/m]  Edge → Compressive and tensile stress fields Screw → Shear stress fields  The energy of a dislocation: approximately from linear elastic theory. Near the dislocation line the distortions are very large and the linear elastic description fails in this region → called the Core of the dislocation (this region range from b to 5b). The energy of the core is about 1/10 the total energy of the dislocation. Energy of dislocation Elastic Non-elastic (Core) E ~E/10

Elastic properties of dislocation 上清充通大睾 DREANOIAI AO TONG UNIVEREITT Strain energy of screw dislocation The elastic energy for screw dislocation stored in this volume per unit length b Yo:= 2πr dW=2πr·dr·L dr du 2 Gb2 822d GLb du dr 4πr Gb R U R In L 4π 4π Yo Institute of Forming Technology Equipment 16

Elastic properties of dislocation Institute of Forming Technology & Equipment 16  The elastic energy for screw dislocation stored in this volume per unit length Strain energy of screw dislocation z x y L r0 r θ dr r b z    2  2 2 1 G z du    dV  2 r dr r GLb du 4 2      u u du 0  dr  L dV r Gb 2 2 2 8  dV  0 2 ln 4 r Gb L R     dr r Gb L 42 R0r 0 2 ln 4 r Gb R L u U s   