
天然晶体,是在大自然中自发结晶形成的,一提起天然晶体,您是否会 想到雪花?雪花晶体就像是“仙女散花”般地从天而落,给人们带来无限的 遐想。可以说,雪花是人们最熟悉的天然晶体之一,有着变化万干的美丽的 形态。而雪花作为晶体,则是枝晶枝晶的典型例子。1611年开普勒 (Kepler)发表《论六角形雪花》时,对雪花形态进行科学思考。他通过观 察与对比,发现所有雪花形态总体上都是六方对称的,但每片雪花形态细节 变化多样。他企图弄清为什么雪花会成六方对称的,但由于当时没有测试晶 体结构的手段,这个秘密没有被解开。 雪花的六角对称的形态有多种多样的不同图案形状,雪花的枝晶具有一 些非平衡系统都具有分维特点。仪态万干的雪花是纯粹天然的杰作,每一朵 雪花内,都有一粒灰尘作为其晶体生长的种子。它们的生长,有着非平衡态 生长的印记。 11
11 天然晶体,是在大自然中自发结晶形成的,一提起天然晶体,您是否会 想到雪花?雪花晶体就像是“仙女散花”般地从天而落,给人们带来无限的 遐想。可以说,雪花是人们最熟悉的天然晶体之一,有着变化万千的美丽的 形态。而雪花作为晶体,则是枝晶枝晶的典型例子。 1611年开普勒 (Kepler)发表《论六角形雪花》时,对雪花形态进行科学思考。他通过观 察与对比,发现所有雪花形态总体上都是六方对称的,但每片雪花形态细节 变化多样。他企图弄清为什么雪花会成六方对称的,但由于当时没有测试晶 体结构的手段,这个秘密没有被解开。 雪花的六角对称的形态有多种多样的不同图案形状,雪花的枝晶具有一 些非平衡系统都具有分维特点。仪态万千的雪花是纯粹天然的杰作,每一朵 雪花内,都有一粒灰尘作为其晶体生长的种子。它们的生长,有着非平衡态 生长的印记

举例:雪花图案:六个角。 对称图形:雪花等同图形:一个角,相等图形 阶次:6对称要素:直线对称动作:旋转 米米米 必 采架 自然界八种雪花的图案
12 举例: 雪花图案:六个角。 对称图形:雪花 等同图形:一个角,相等图形 阶次:6 对称要素:直线 对称动作:旋转 自然界八种雪花的图案

早在公元前的西汉时代,《韩诗外传》中就指出: “凡草木花多五出,雪花独六出。”雪的基本形状是六角 形。但在不同的环境下,却可表现出各种样的形态。 世界上有不少雪花图案收集者,他们收集了各种雪 花图案。有人花了毕生精力拍摄了成干上万张雪花照片, 发现将近有六干种彼此不同的雪花,但他死前认为这不过 是大自然落到他手中的少部分雪花而已。以致于有人说没 有两朵大小和形状完全相同的雪花。 (http://news.xinhuanet.com/forum/2005-01/30/content 2519823.htm) 13
13 早在公元前的西汉时代,《韩诗外传》中就指出: “凡草木花多五出,雪花独六出。”雪的基本形状是六角 形。但在不同的环境下,却可表现出各种样的形态。 世界上有不少雪花图案收集者,他们收集了各种雪 花图案。有人花了毕生精力拍摄了成千上万张雪花照片, 发现将近有六千种彼此不同的雪花,但他死前认为这不过 是大自然落到他手中的少部分雪花而已。以致于有人说没 有两朵大小和形状完全相同的雪花。 (http://news.xinhuanet.com/forum/2005-01/30/content _2519823. htm)
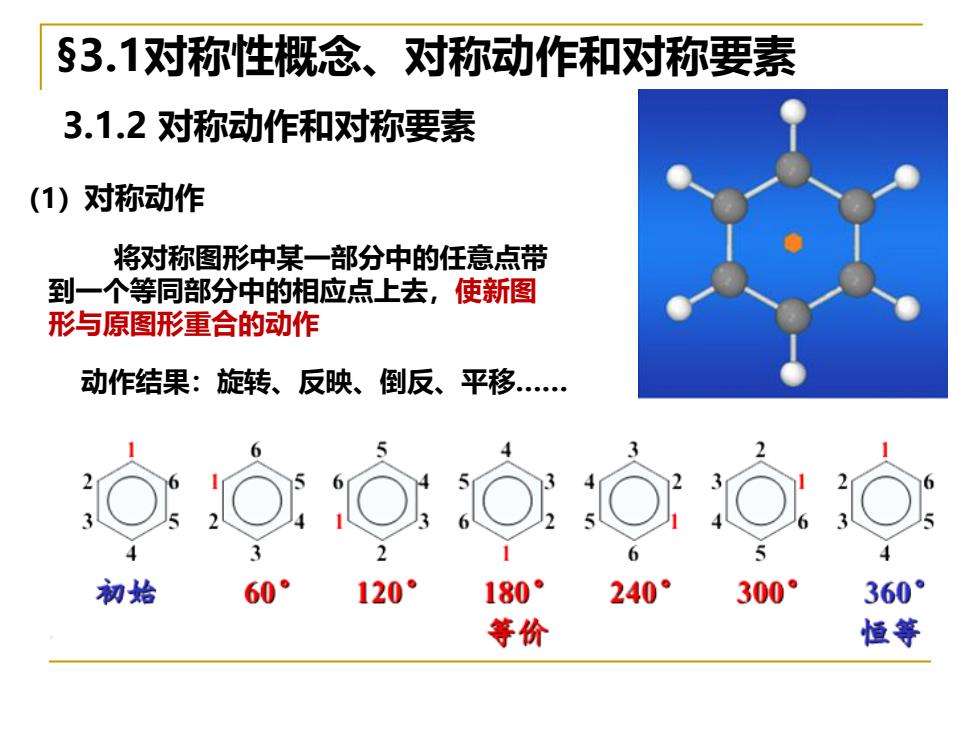
§3.1对称性概念、对称动作和对称要素 3.1.2对称动作和对称要素 (1)对称动作 将对称图形中某一部分中的任意点带 到一个等同部分中的相应点上去,使新图 形与原图形重合的动作 动作结果:旋转、反映、倒反、平移. ⊙⊙⊙⊙⊙:⊙:⊙ 初始 60° 120° 180 240° 300° 360° 等价 恒等
3.1.2 对称动作和对称要素 (1)对称动作 将对称图形中某一部分中的任意点带 到一个等同部分中的相应点上去,使新图 形与原图形重合的动作 动作结果:旋转、反映、倒反、平移. §3.1对称性概念、对称动作和对称要素
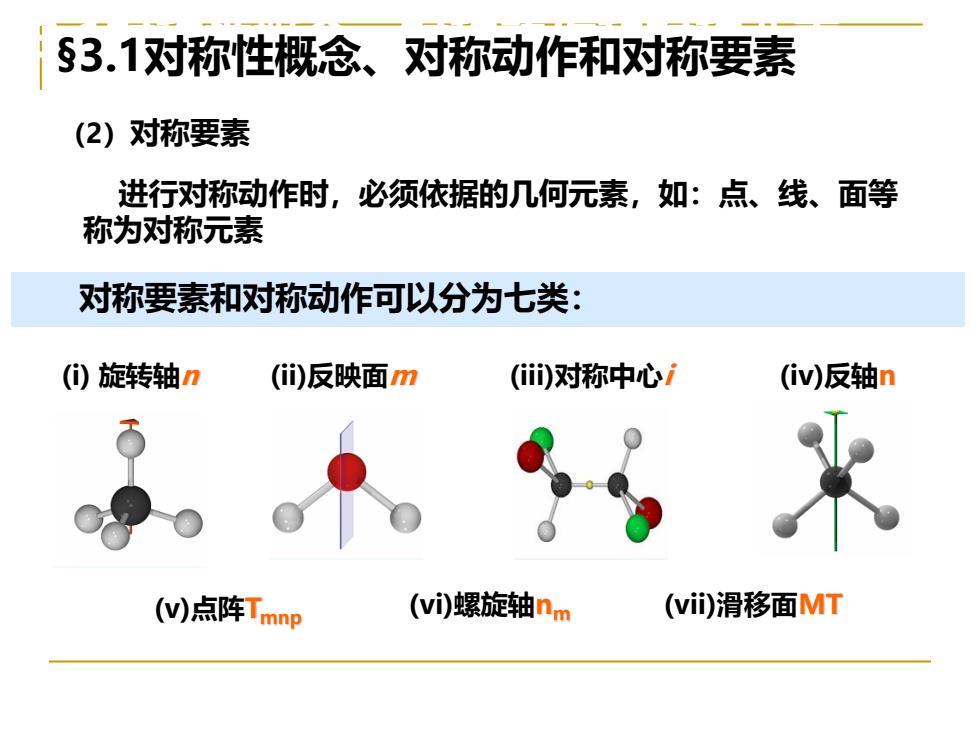
§3.1对称性概念、对称动作和对称要素 (2)对称要素 进行对称动作时,必须依据的几何元素,如:点、线、面等 称为对称元素 对称要素和对称动作可以分为七类: ()旋转轴n ()反映面m (i)对称中心i (iv)反轴n ()点阵Tmnp (i螺旋轴nm (vi)滑移面MT
§3.1对称性概念、对称动作和对称要素 (2)对称要素 进行对称动作时,必须依据的几何元素,如:点、线、面等 称为对称元素 (i) 旋转轴n (ii)反映面m 对称要素和对称动作可以分为七类: (iii)对称中心i (v)点阵Tmnp (iv)反轴n (vi)螺旋轴nm (vii)滑移面MT §3.1对称性概念、对称动作和对称要素