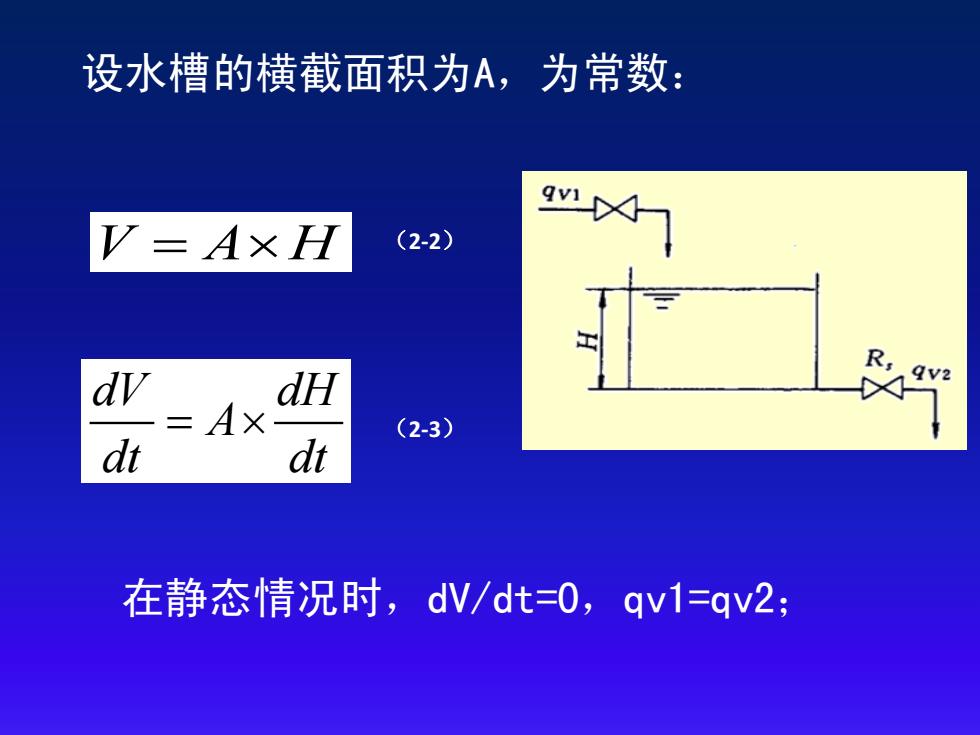
设水槽的横截面积为A,为常数: V=A×H (2-2) dy dH 9V2 Ax (2-3) dt dt 在静态情况时,dV/dt=0,qv1=qv2;
设水槽的横截面积为A,为常数: V A H (2-2) dV dH A dt dt (2-3) 在静态情况时,dV/dt=0,qv1=qv2;

当qv1发生变化时,液位H将随之变化,水 槽出口处的静压也随之发生变化,流出量q2 亦发生变化。 流出量qV2与液位H成正比,与出水阀对水 的阻力Rs成反比,即: 92= H (2-4) Rs R ,9v2 若出水阀开度不变,阻 力Rs为常数
当qv1发生变化时,液位H将随之变化,水 槽出口处的静压也随之发生变化,流出量qv2 亦发生变化。 流出量qv2与液位H成正比,与出水阀对水 的阻力Rs成反比,即: 2 H qv Rs (2-4) 若出水阀开度不变,阻 力Rs为常数
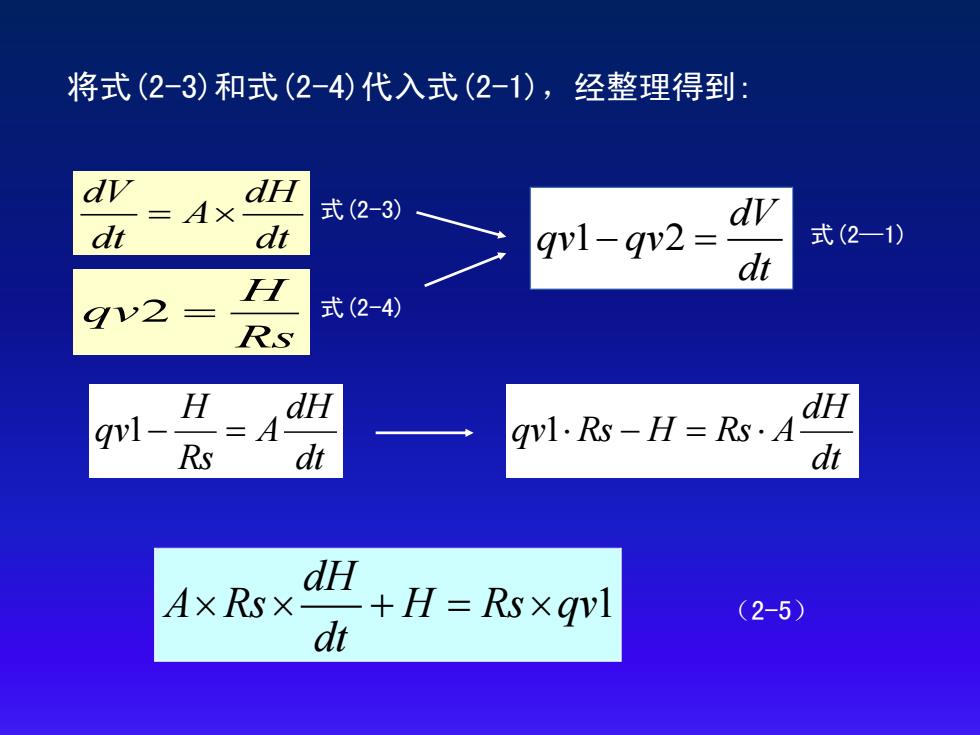
将式(2-3)和式(2-4)代入式(2-1),经整理得到: d dH =Ax 式(2-3) dt dt qv1-gv2= 式(2一1) dt gv2 式(2-4) Rs H =4 H H qwl·Rs-H=Rs·A Rs dt dt d A×Rsx dt H+H=Rs×qI (2-5)
将式(2-3)和式(2-4)代入式(2-1),经整理得到: dV dH A dt dt 2 H qv Rs 1 2 dV qv qv dt 1 dH A Rs H Rs qv dt (2-5) dt dH A Rs H qv1 dt dH qv1Rs H Rs A 式(2-3) 式(2-4) 式(2—1)

dH A×Rsx +H=Rs×qwl (2-5) dt T-ARs,K-Rs 代入(2-5),得到: dH T× i+H=K×ql (2-6) dt 式中 T-一-一时间常数 K--一被控对象的放大系数
1 dH A Rs H Rs qv dt (2-5) 令 T ARs K Rs , 代入(2-5),得到: 1 dH T H K qv dt (2-6) 式中: T----时间常数 K----被控对象的放大系数

dH T× dt +H=K×ql 上式描述了单容水槽输入量qv1与输出量H 之间的数学关系,称为被控对象的数学模型, 为一阶常系数微分方程式。 称被控对象为: 一阶被控对象 R 9V2
上式描述了单容水槽输入量qv1与输出量H 之间的数学关系,称为被控对象的数学模型, 为一阶常系数微分方程式。 称被控对象为: 一阶被控对象 1 dH T H K qv dt