以水槽液位为例,分析推导被控对象的数学描述形式。 建立被控对象的数学模型(输入 输出) 物料平衡和能量平衡(在连续生产过程中) R: 9V2
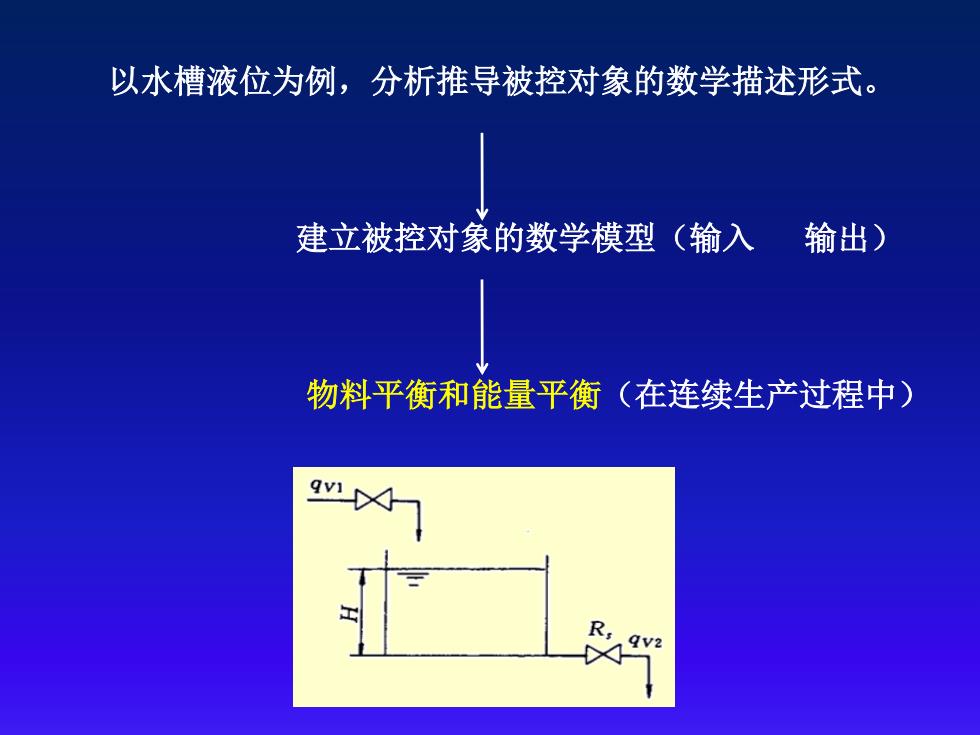
以水槽液位为例,分析推导被控对象的数学描述形式。 建立被控对象的数学模型(输入 输出) 物料平衡和能量平衡(在连续生产过程中)
◆在静态条件下,流入对象的物料(或 能量)等于从系统中流出的物料(或能量): ◆在动态条件下,单位时间内流入对象的物料与 单位时间内从系统中流出的物料之差,等于系 统内物料(或能量)贮存量的变化率。 被控对象的数学描述: 由这两种关系推导出来的微分方程。即建立被控对象的数学模型
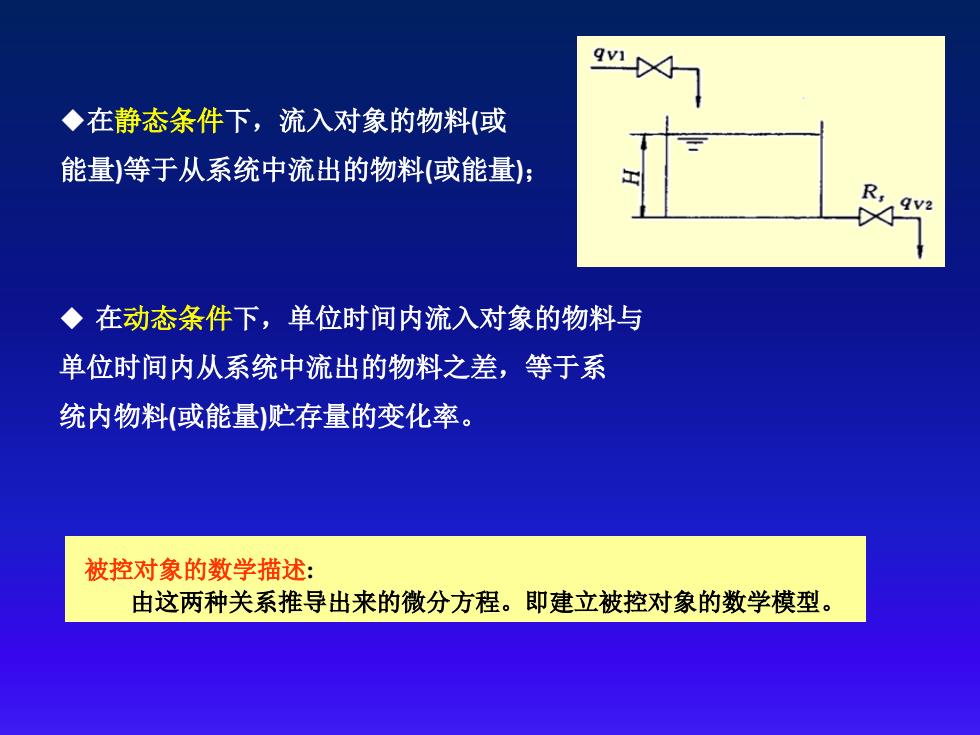
在动态条件下,单位时间内流入对象的物料与 单位时间内从系统中流出的物料之差,等于系 统内物料(或能量)贮存量的变化率。 在静态条件下,流入对象的物料(或 能量)等于从系统中流出的物料(或能量); 被控对象的数学描述: 由这两种关系推导出来的微分方程。即建立被控对象的数学模型
被控对象数学模型的建立 利用能量平衡或物料平衡建立被控对象的数学模 型一机理建模法 1.单容液位对象 (1)有自衡特性的单容对象 R, 有自衡特性液位变化曲线 水槽输入变量:qV1 A一一流量曲线 水槽输出变量:H B一一高位槽液位曲线
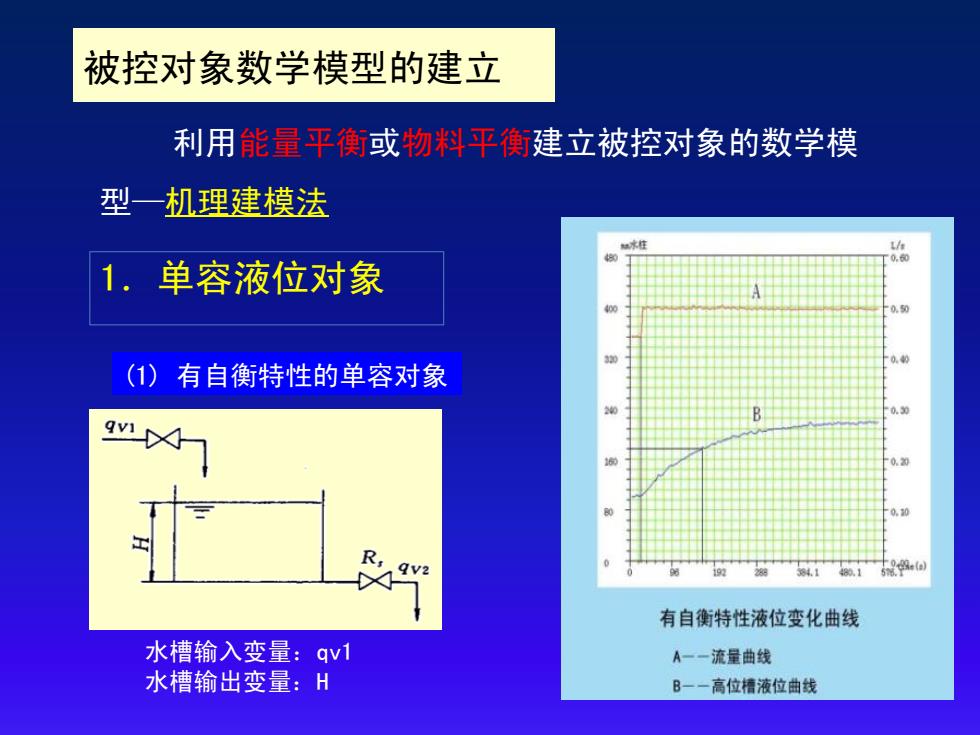
1.单容液位对象 (1) 有自衡特性的单容对象 水槽输入变量:qv1 水槽输出变量:H 利用能量平衡或物料平衡建立被控对象的数学模 型—机理建模法 被控对象数学模型的建立

H--液位(输出变量) qv1--水槽的进水流量, 由管路上的阀1来调节; qv2--水槽的出水流量, 由管道上阀2的开度来控制, 为操纵变量。 qv1、qv2--体积流量
H---液位 (输出变量) qv1---水槽的进水流量, 由管路上的阀1来调节; qv2---水槽的出水流量, 由管道上阀2的开度来控制, 为操纵变量。 qv1、qv2---体积流量

在任何时刻水位的变化均满足下面的物料平衡关系: gvl-gv2 (2-1) dt 式中: 一水槽内液体的贮存量(液体的体积); t一时间; dV/dt—贮存量的变化率。 R
1 2 dV qv qv dt (2-1) 式中: V——水槽内液体的贮存量(液体的体积); t——时间; dV/dt——贮存量的变化率。 在任何时刻水位的变化均满足下面的物料平衡关系: